





- 【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——《有理数及其运算》期末复习精讲精练(教案) 教案 1 次下载
- 【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——《有理数及其运算》期末复习精讲精练(练习) 试卷 4 次下载
- 【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——压轴题系列一《线段的动点问题》期末复习精讲精练(教案) 教案 1 次下载
- 【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——压轴题系列一《线段的动点问题》期末复习精讲精练(练习) 试卷 2 次下载
- 【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——压轴题系列一《线段的动点问题》期末复习精讲精练(课件) 课件 2 次下载
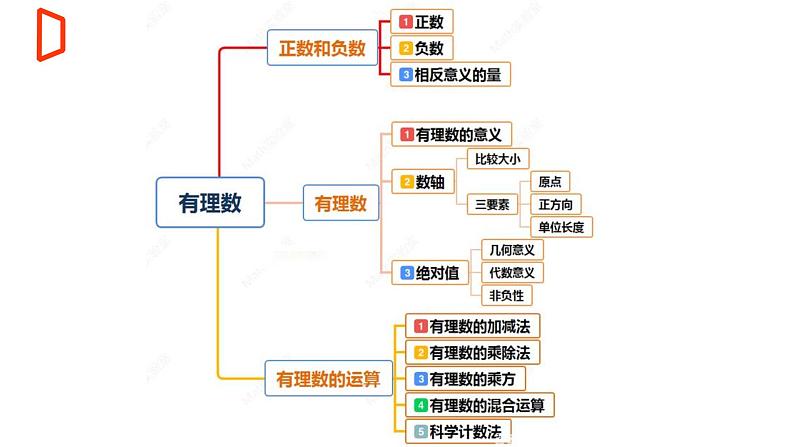
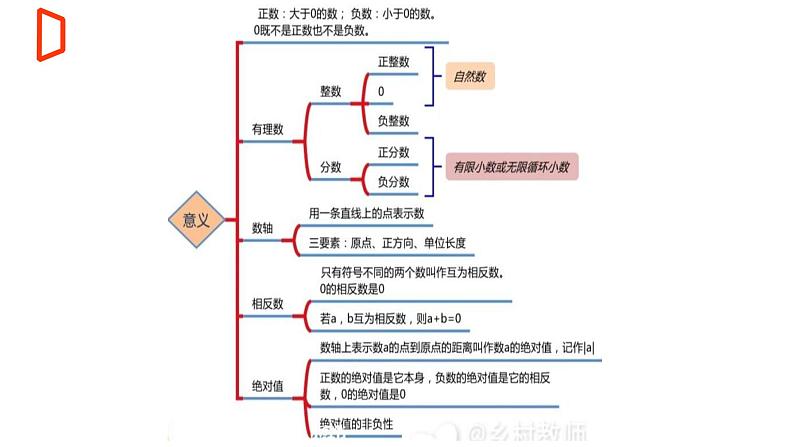
【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——《有理数及其运算》期末复习精讲精练(课件)
展开一、 双基目标 1、深刻理解有理数相关概念及其代数、几何意义;2、理解并熟练掌握有理数的“+、-、×、÷、乘方”五类运算法则及运算方法;3、熟练掌握有理数运算的各类应用.
二、能力目标建立在有理数分类、数轴及相关概念基础上的有理数运算在整个初中阶段极其重要,运算能力强弱直接关乎后续八九年级的数学学习成绩的优劣,以及学生数学能力的发展潜力。所以,针对其中的运算能力、分类思想、数学结合思想等的培养和强化尤为关键!
有理数的相关概念及意义
《九章算术》中注有“今两算得失相反,要令正负以名之”.大意是:今有两数若其意义相反,则分别叫做正数与负数.若水位上升2m记作+2 m,则下降1m记作 m.
【答案】 -1 【考点】正数和负数的认识及应用 【解析】【解答】解: ∵水位上升 2m 记作+2m , ∴下降 1m 记作 -1m .故答案为: -1
几种气体的液化温度(标准大气压)如下表:
其中液化温度最高的气体是( )A. 氦气 B. 氮气 C. 氢气 D. 氧气
【解析】【解答】解:由题意得: ∵
∴ ;∴液化温度最高的气体是氧气;故答案为:D.
检测4个排球,其中超过标准的克数记为正数,低于标准的克数记为负数,从轻重的角度来看,最接近标准的球是( B ) A. B. C. D.
下列判断错误的是( ) A. 3>﹣5 B. ﹣3>﹣5 C. ﹣2.5>﹣|﹣2.25| D >
如图,数轴上点A,B分别对应有理数a,b,则下列结论正确的是( )
A. a>b B. |a|>|b| C. a+b>0 D. ﹣a>b
在数轴上,点 A 表示 -2 ,从点A 出发,沿数轴移动5个单位长度到达点B,则点B表示的数是 .
下列说法中,错误的是( ) A. 数轴上表示 -3的点距离原点3个单位长度 B. 规定了原点、正方向和单位长度的直线叫做数轴C. 有理数0在数轴上表示的点是原点 D. 表示十万分之一的点在数轴上不存在
【解答】当点A向右移动时,B点表示的数是-2+5=3 ; 当点A向左移动时,B点表示的数是 -2-5=-7 ;故答案是:3或 -7 .
若数轴上点A 表示-1,且 AB=3 ,则点B 表示的数是( ) A. -4 B. 2 C. -3或3 D. -4或2
【答案】 D 【考点】数轴及有理数在数轴上的表示 【解析】【解答】解:当点B在点A左侧时,点B表示的数为-1-3=-4, 当点B在点A右侧时,点B表示的数为-1+3=2,∴点 B表示的数是-4或2,故答案为:D.
下列说法中,正确的是( ) A. -a 一定是负数 B. 若 ,则 a=0.5 C. -a 的倒数是 D. a与 -a 互为相反数
相反数、绝对值、倒数的意义
【解答】解:A、a表示一个实数,可以是正数或负数或零,A不符合题意, B、|a|=0.5,则a=0.5或−0.5,B不符合题意,C、a表示一个实数,可以是正数或负数或零,零没有倒数,选项C不符合题意,D、a与−a互为相反数,选项D符合题意.故答案为:D.
已知 a 、 b互为相反数, c 是绝对值最小的数, d 是负整数中最大的数,则 a+b-c+d .
若a、b互为相反数,c、d互为倒数,则求(a+b)2021 -(cd)2022值.
解:根据题意得a+b=0、cd=1,
【分析】根据“a、b互为相反数,c、d互为倒数”可得a+b=0,cd=1,再将a+b=0,cd=1代入 (a+b)2021 -(cd)2022 计算即可。
【分析】根据“a、 b 互为相反数, c 是绝对值最小的数, d是负整数中最大的数”可得a+b=0,c=0,d=-1,再代入a+b-c+d计算即可。【答案】:1
下列数中:2,1.0010001, ,0,﹣π,有理数的个数是( ) A. 2个 B. 3个 C. 4个 D. 5个
【解答】解:2,1.0010001,
,0,﹣π,中, 2,0为整数,属于有理数,
1.0010001,为有限小数,属于有理数,为分数,属于有理数,∴有理数有 4个,故答案为:C.
在下列数: ,+1,6.7,-15,-1中,属于分数的有( ) A. 2个 B. 3个 C. 4个 D. 5个
【解答】解: 是分数,符合题意;+1是正整数,不是分数,不符合题意;6.7是有限小数,是分数,符合题意;-15和-1都是负整数,不是分数,不符合题意, ∴分数一共有2个,故答案为:A.
【答案】 C 【解析】【解答】解:∵-2021<0, ∴|−2021| =-(-2021)=2021,故答案为:C.
绝对值不大于2的整数有 个
【分析】绝对值不大于2的整数有+2,±1,0,共5 个.把它们按从小到大排列即可.【解答】解∶绝对值不大于2的整数有+2,±1,0,共5个.它们按从小到大排列为∶-2,-1,0,1,2. 点评∶注意∶0的绝对值还是0.
“东风快递,使命必达!”东风-41是我国目前最先进的洲际战略导弹,假设其最快飞行速度是25马赫,若每马赫速度为340米/秒,则用科学记数法表示东风-41的最快飞行速度为( ) A. 8.5×103米/秒 B. 0.85×104米/秒 C. 8.5×104米/秒 D. 85×103米/秒
【解答】解:最快飞行速度=25×340=8500米/秒=8.5×103米/秒. 故答案为:A.
2021年5月15月07时18分,“天问一号”火星探测器成功登陆火星表面,开启了中国人自主探测火星之旅.地球与火星的最近距离约为5460万公里.“5460万”用科学记数法表示为( )
【解答】解:∵5460万=54600000, ∴
科学记数法的表示形式为a×10n,其中1≤a<10,n为正整数,表示时关键要确定a的值以及n的值.
有理数的运算主要把握三点:一、是运算法则,二、是运算顺序.三、能运用运算律的,要运用运算律简化运算.
两个有理数的和为正数,那么这两个数一定( ) A. 都是正数 B. 至少有一个正数 C. 有一个是0 D. 绝对值不相等
【解答】解:根据有理数的加法法则可知:如果两个有理数的和是正数,那么这两个数有三种情况:同正或一正一负且正数的绝对值大于负数的绝对值或一个正数和0.显然三种情况中,至少一个为正数. 故答案为:B.
下列计算中,正确的是( ) A. B. C. D.
下列各组的两个数中,运算后的结果相等的是( ) A. (﹣2)3和(﹣3)2 B. (﹣2)3和﹣23 C. (﹣2)2和﹣22 D. 23和32
如图,数轴上A 、B 两点分别对应 a 、 b ,则下列结论正确的是( )A. a+b>0 B. ab>0 C. a-b>0 D.
【解答】解:由a,b两数在数轴上表示点的位置,可知b<0<a,且 ,可得: A、a+b<0,所以选项A不符合题意; B、ab<0,所以选项B不符合题意;C、a-b>0,所以选项C符合题意;D、 ,所以选项D不符合题意;故答案为:C.
如果a+b>0,且ab<0,那么( ) A. a>0,b>0 B. a<0,b<0 C. a、b异号 D. a、b异号且正数的绝对值较大
【解答】解:根据题意,ab<0,则a、b异号, a+b>0可得,正数的绝对值较大,但无法确定a、b哪个为正,哪个为负,故答案为:D.
有理数a,b在数轴上的对应点如图,下列式子:① a>0>b ; ② ;③ ab<0 ;④a-b>a+b ;⑤ ,其中错误的个数是( ) A. 1 B. 2 C. 3 D. 4
【解答】解:如图: 由数轴可得:a<0<b,且|a|>|b|①由a<0<b可知,a>0>b不符合题意;②由|a|>|b|可知|b|>|a|不符合题意;③由a,b异号,可知ab<0符合题意;④由b>0,可知a-b>a+b不符合题意;⑤由a<0<b,|a|>|b|,则 ,符合题意;∴错误的有3个;故答案为:C.
反思:1、区分清楚(-a)2和-a2不同的运算意义; 2、分清有理数混合运算顺序——先算括号,后算乘除,最后算加减.
注意去括号要变号!!!
已知|x|=3,|y|=2,且xy > 0,则x−y的值等于 .
【解答】解:∵|x|=3,|y|=2,且xy > 0, ∴x=3,y=2或x=−3,y=-2,则x−y=1或−1.故答案为:1或−1.
若∣a|=7、b2=4,且∣a-b∣=∣a∣+∣b|,则a+b的值为 .
【解答】解:∵|a|=7,b2=4, ∴a=±7,b=±2,当a=7,b=2时,∴|a−b|=5,|a|+|b|=9,不符合题意,舍去.当a=7,b=−2时,∴|a−b|=9,|a|+|b|=9,符合题意,∴a+b=5.
当a=−7,b=2时,∴|a−b|=9,|a|+|b|=9,符合题意.∴a+b=−5,当a=−7,b=−2时,∴|a−b|=5,|a|+|b|=9,不符合题意,舍去.故答案为:±5.
(1)一个数的绝对值是指在数轴上表示这个数的点到 的距离. (2)若 ,则a 0.(3)有理数a,b在数轴上的位置如图所示,请化简
(3)解:由各点在数轴上位置可知,
某路公交车从起点经过A,B,C,D 站到达终点,各站上、下乘客人数如下表所示(用正数表示上车的人数,负数表示下车的人数) 若此公交车采用一票制,即每位上车乘客无论哪站下车,车票都是2元,问该车这次出车共收入( )A. 114元 B. 228元 C. 78元 D. 56元
则该车这次出车共收入114元.故答案为:A
2020 年的“新冠肺炎”疫情的蔓延,市场上医用口罩销量大幅增加,某口罩加工厂为满足市场需求,计划每天生产6000个,由于各种原因与实际每天生产量相比有出入,下表是三月份某一周的生产情况(超产为正,减产为负,单位:个).
(1)产量最多的一天比产量最少的一天多生产多少个; (2)与原计划产量比较,这一周产量超产或减产多少个? (3)若口罩加工厂实行计件工资制,每生产一个口罩0.2元,则本周口罩加工厂应支付工人的工资总额是多少元?
【答案】 (1)解: (个) 答:产量最多的一天比产量最少的一天多生产500个;
(2)解: (个) 则:这一周产量超产500个;
(3)解: (元) 答:本周口罩加工厂应支付工人的工资总额是8500元.
某公路检修队乘车从A地出发,在南北走向的公路上检修道路,规定向南走为正,向北走为负,从出发到收工时所行驶的路程记录如下(单位:千米):+2,-8,+5,-7,+10,-6,-7,+12. (1)收工时,检修队在A 地的哪边?距 A地多远? (2)在汽车行驶过程中,若每行驶1千米耗油0.2升,则检修队从 A地出发到回到 A地,汽车共耗油多少升? (3)请直接回答出在检修过程中,检修队最远离 A地多远?
“数形结合”是重要的数学思想.如: 表示 3 与 -2 差的绝对值,实际上也可以理解为 3 与 -2 在数轴上所对应的两个点之间的距离.进一步地,数轴上两个点A,B所对应的数分别用 a , b 表示,那么A,B两点之间的距离表示为
.利用此结论,回答以下问题:
(1)数轴上表示 -2 和 5 两点之间的距离是 .
可理解为 与 两数在数轴上所对应的两点之间的距离;
可理解为 与 两数在数轴上所对应的两点之间的距离.
(3)若 ,则 x= .
(4)若 x 表示一个有理数, 的最小值为 .
(5)直接写出所有符合条件的整数x,使得 , x的值为 .
(1)数轴上表示 -2 和 5 两点之间的距离是 .
可理解为 与 两数在数轴上所对应的两点之间的距离;
可理解为 与 两数在数轴上所对应的两点之间的距离.
(3)若 ,则 x= .(4)若 x 表示一个有理数, 的最小值为 .
(5)直接写出所有符合条件的整数x,使得 , x的值为 .
数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为 .根据以上知识解题:
(1)若数轴上两点A、B表示的数为-2、3,则|AB|= ; (2)若数轴上两点A、B表示的数为x、-1, ①A、B之间的距离可用含x的式子表示为 ;②若该两点之间的距离为2,那么x值为 ;
(3)|x+1|+|x-2|的最小值为 .
【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——第二课《整数的加减篇》期末复习精讲精练(课件): 这是一份【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——第二课《整数的加减篇》期末复习精讲精练(课件),共34页。PPT课件主要包含了典例精讲,解答解,跟踪练习,解原式,3a+3b-3ab,3y2-2xy,知识回顾,特征条件代入求值,例10,例11等内容,欢迎下载使用。
【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——第三课《规律探索问题精讲》期末复习精讲精练(课件): 这是一份【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——第三课《规律探索问题精讲》期末复习精讲精练(课件),共27页。PPT课件主要包含了典例精讲,数图法,答案3n,分类法,跟踪练习,3n+1,n+1,去重法,4n+2,补形法等内容,欢迎下载使用。
【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——压轴题系列二《角的几何变换——折叠与旋转》期末复习精讲精练(课件): 这是一份【期末满分冲刺】2022-2023学年-北师大版数学七年级上册——压轴题系列二《角的几何变换——折叠与旋转》期末复习精讲精练(课件),共35页。PPT课件主要包含了典例精讲,20°或80°,跟踪练习等内容,欢迎下载使用。













