解决几何图形最值问题的方法（二）---代数方法(教师版)附答案

这是一份解决几何图形最值问题的方法（二）---代数方法(教师版)附答案，共11页。试卷主要包含了知识要点，题型等内容，欢迎下载使用。
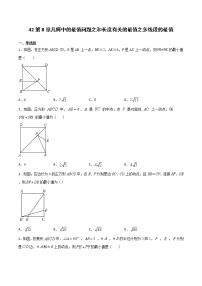
解决几何图形最值问题的方法（二）附答案---代数方法一、知识要点：几何图形最值问题是近年来各类考试的常考题型，解决这类问题的方法大致有两类，（1）几何方法：利用几何图形的性质求最值.（2）代数方法：借助题目中几何图形的性质建立两个相关变量间的函数关系式，并能通过函数的最值来探求图形中某些元素的最值。二、题型：（一）利用配方法求几何图形最值1．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE，那么DE长的最小值是　        　． 【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=x，CD′=，根据勾股定理然后用配方法即可求解．解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=x，CD′=（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=x2+（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．2．如图，正方形边长为4，，分别是边，上的两个动点且，则的最小值是（　　）A．4   B．5   C．   D．解：∵，∴而，∴又∵，∴∽∴若设，则于是有，∴∴即：当时，取最小值为3，而，又为定值，所以当取最小值时，取最小值此时即当取最小值3时，取最小值5．故选：B．3．在平面直角坐标系中，已知，，为轴上的动点，以为边构造，使点在轴上，，为的中点，则的最小值为（　　）A．    B．   C．   D．解：如图，过点作轴于，过点作于，则四边形是矩形，∴，∵，∴，，∴，∴∽，∴，即，∴，设，则，∴，，∴，，∵，∴，∵，∴，∴的最小值为，故选：C．4．如图，在中，，是边上不同于的一动点，过点作，垂足为，连接．若，，则的面积的最大值是（　　）A．    B．    C．    D．解：设，由勾股定理得，∵，，∴∽，∴，即∴，，∴当时，的面积最大，最大值是．故选：C．5．如图，已知边长为10的正方形，是边上一动点（与、不重合），连接，是延长线上的点，过点作的垂线交的角平分线于点，若．（1）求证：∽；（2）若，求的面积；（3）请直接写出为何值时，的面积最大．【分析】（1）利用同角的余角相等，判断出，进而得出∽，即可得出结论；（2）先求出，进而表示出，由∽，得出，求出，最后用三角形面积公式即可得出结论；（3）同（2）的方法，即可得出，即可得出结论．解：（1）∵四边形是正方形，，∴，∴，，∴，∵，∴∽；（2）∵，，∴，∵，∴，由（1）知，∽，∴，∴，∴，∴；（3）设，则，∴，由（1）知，∽，∴，∴，∴，∴，当时，的最大值为．6.如图1，矩形中，，，把矩形沿直线折叠，使点落在点处，交于点，连接．(1)求证:；(2)求的值；(3)如图2，若为线段上一动点，过点作的内接矩形，使其定点落在线段上，定点、落在线段上，当线段的长为何值时，矩形的面积最大？并求出其最大值．解析:(1)证明:由矩形的性质可知，∴，，，在与中∴；(2)解:如图1，∵，∴，设，则，在中，，即，解得；，即．(3)解:如图2，由矩形的性质得∴又∵，设，则，即过作于，则，]∴又∵在中，，解得∴，即设矩形的面积为则所以当，即时，矩形的面积最大，最大面积为3．（二）利用判别式求几何图形最值1. 如图，在中，，，，点为边上的一个动点，连接，过点作交边于点，则的最大值为________．    解：过作于，过作于， ∵在中，，， ，∴，∴，，∵，，∴，∴，，设，，∴，，∴，∵，∴，∴，∴，∴∽，∴，∴∴，∵方程有实数解，∴，∴，整理得，，解得或（舍去），∴，∴的最大值为2．故答案为2．【分析】过作于，过作于，利用相似三角形的性质根据一元二次方程，利用根的判别式解决问题即可．2. 如图．直线与坐标轴相交于、两点，动点在线段上，动点在线段上、连结，且满足，则当______度时，线段的最小值为______．解：如图，过点作于点，过点作于点，设，∵直线与坐标轴相交于、两点，，，，，，，，，，，，，，，在 中, ,,在 中，，，,整理得, ,，,,解得, 舍去 或 , 的最小值为 2 , 的最小值为 2 , 此时 ,,∴故答案为：30,2点评：本题考查相似三角形的判定和性质，一元二次方程的根的判别式等知识，学会添加常用辅助线，构造相似三角形解决问题是解题的关键．