2022-2023学年人教版九年级上学期数学期末达标测试卷（B卷）

2022-2023学年人教版九年级上学期数学期末

达标测试卷（B卷）

【满分：120分】

一、选择题：（本大题共12小题，每小题3分，共36分，给出的四个选项中，只有一项是符合题目要求的）

1.已知函数 是二次函数，则m等于(   )

A. B.2 C.-2 D.

2.若关于x的方程有两个不相等的实数根，则实数a的取值范围是(   )

A. B. C. D.

3.在平面直角坐标系中，点与点关于原点成中心对称，则的值为(   )

A.-3 B.-1 C.1 D.3

4.从1，2，3，4，5这五个数中任选两个数，其和为偶数的概率为(   )

A. B. C. D.

5.如图，是等边三角形ABC的内切圆，分别切AB，BC，AC于点E，F，D，P是上一点，则的度数是(   )

A.65° B.60° C.58° D.50°

6.定义表示不超过实数x的最大整数,如.函数的图象如图所示,已知,则方程的解为(   )

A.0或 B.0或1 C.1或 D.或

7.如图，与的边AB相切，切点为B，将绕点B按顺时针方向旋转得到，使点落在上，边交线段AO于点C，若，则为(   )

A.85° B.87.5° C.88° D.90°

8.如图，以边长为2的等边顶点A为圆心、一定的长为半径画弧，恰好与BC边相切，分别交AB，AC于D，E，则图中阴影部分的面积是(   )

A. B. C. D.

9.当时，二次函数有最大值4，则实数m的值为(   )

A. B.或 C.2或 D.2或或

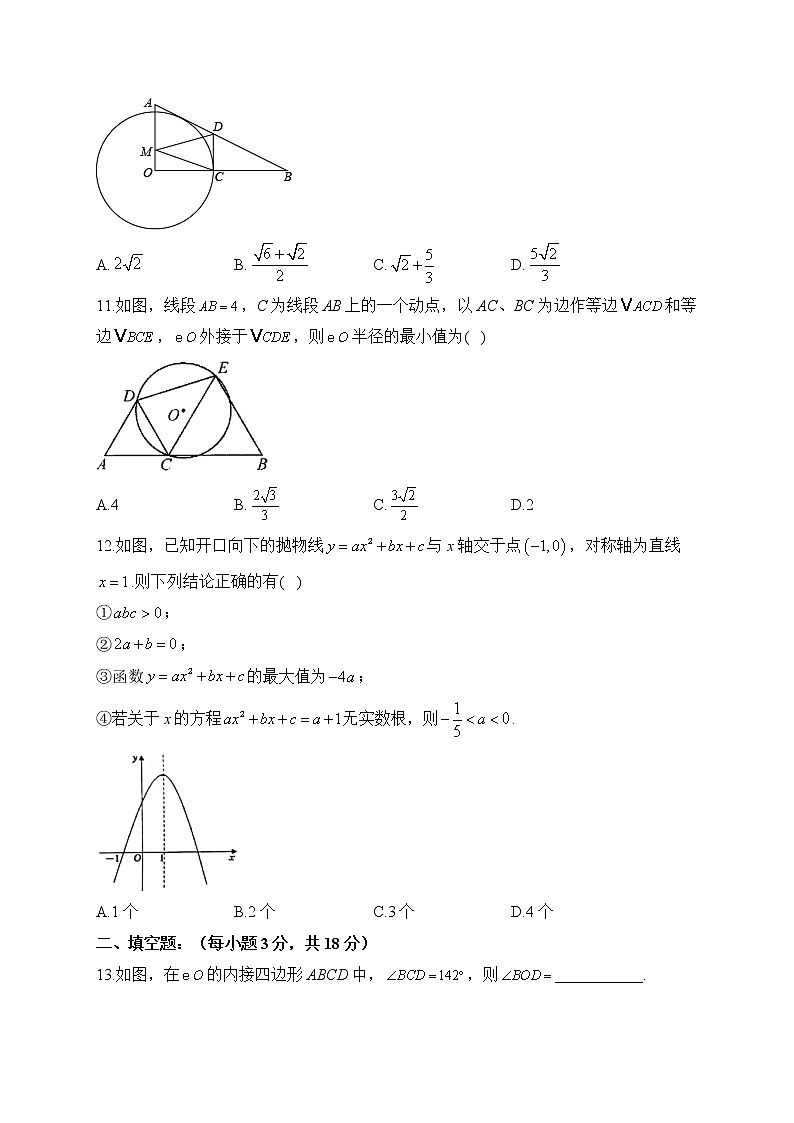
10.如图，在中，，，半径为1的与OB交于点C，且AB与相切，过点C作交AB于点D，点M是边OA上动点.则周长最小值为(   )

A. B. C. D.

11.如图，线段，C为线段AB上的一个动点，以AC、BC为边作等边和等边，外接于，则半径的最小值为(   )

A.4 B. C. D.2

12.如图，已知开口向下的抛物线与x轴交于点，对称轴为直线.则下列结论正确的有(   )

①；

②；

③函数的最大值为；

④若关于x的方程无实数根，则.

A.1个 B.2个 C.3个 D.4个

二、填空题：（每小题3分，共18分）

13.如图，在的内接四边形ABCD中，，则___________.

14.已知，则____________.

15.有三张完全一样、正面分别写有字母A，B，C的卡片.将其背面朝上并洗匀，从中随机抽取一张，记下卡片上的字母后放回洗匀，再从中随机抽取一张，则抽取的两张卡片上的字母相同的概率是_________.

16.将抛物线绕它的顶点旋转180°后，所得抛物线的表达式是________________.

17.如图，已知抛物线与x轴交于A、B两点，与y轴交于点C，顶点为D，其中点B坐标为，顶点D的横坐标为1，轴，垂足为E，下列结论：①当时，y随x增大而减小；②；③；④；⑤当时，.其中结论正确的有______.（填序号）（多填错填倒扣一分）

18.如图，已知中，，，，则经过A，B，C三点的的长度为______.

三、解答题（本大题共8小题，共计66分，解答题应写出演算步骤或证明过程）

19.（6分）如图，在平面直角坐标系中，A，B，C三点的坐标依次为，，.根据题意，解答下列问题.

(1)画出关于原点O成中心对称的；

(2)把绕点顺时针旋转90°得到；

(3)连接，和，直接写出的面积.

20.（6分）关于x的一元二次方程有两个实数根，.

(1)求k的取值范围；

(2)是否存在实数k，使得和互为相反数？若存在，请求出k的值；若不存在，请说明理由.

21.（8分）在平面直角坐标系中，二次函数(b，c都是常数)的图象经过点和.

(1)当时，求y的取值范围.

(2)已知点在该函数的图象上，且，求点P的坐标.

22.（8分）梦想商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，如果每件提价1元出售，其销售量就减少20件.

(1)假设提价10元，则销售量为_________件，提价x元，则销售量为___________件；

(2)现在获利12000元，且销售成本不超过24000元，问这种服装销售单价应定多少元？这时应进多少服装？

(3)当销售单价应定多少元时，该商店获得最大利润？最大利润是多少元？

23.（8分）如图所示，AB是的直径，点P是AB延长线上的一点，过点P作的切线，切点为C，连接AC，BC.

（1）求证：.

（2）若点P在AB的延长线上运动，的平分线交AC于点D，你认为的大小是否会发生变化？若变化，请说明理由；若没有变化，求出的大小.

24.（8分）某班甲、乙两名同学被推在到学校艺术节上表演节目，计划用葫芦丝合奏一首乐曲，要合奏的乐曲是用游戏的方式在《月光下的凤尾竹》与《彩云之南》中确定一首.

游戏规则如下；在一个不透明的口袋中装有分别标有数字1，2，3，4的四个小球（除标号外，其余都相同），甲从口袋中任意摸出1个小球，小球上的数字记为a.在另一个不透明的口袋中装有分别标有数字1，2的两张卡片（除标号外，其余都相同），乙从口袋里任意摸出1张卡片，卡片上的数字记为b.然后计算这两个数的和，即.若为奇数，则演奏《月光下的凤尾竹》，否则，演奏《彩云之南》.

（1）用列表法或画树状图法中的一种方法，求所有可能出现的结果总数；

（2）你认为这个游戏公平吗?如果公平，请说明理由;如果不公平，哪一首乐曲更可能被选中?

25.（10分）如图，AB是的直径，点D在AB的延长线上，C、E是上的两点，且，，延长AE交BC的延长线于点F.

（1）求证：CD是的切线；

（2）求证：；

（3）若，求的面积.

26.（12分）抛物线经过，，与y轴交于点，对称轴为.

(1)求此抛物线的解析式；

(2)D为抛物线上一点(不与点C重合)，若，求点D的坐标；

(3)点Q为对称轴右侧抛物线上一点，若以BQ为斜边的等腰直角三角形PBQ的顶点P落在对称轴上，求点Q的坐标.

答案以及解析

1.答案：B

解析：是二次函数，

，且，

.

故答案选B.

2.答案：C

解析：根据题意可得：，

解得：.

故选：C.

3.答案：C

解析：点与点关于原点成中心对称，，，，故选：C.

4.答案：B

解析：画树状图如图：

共有20种等可能的结果，

其中两个数的和为偶数的有，，，，，，，，共8种，

这五个数中任选两个数的和为偶数的概率为.故选：B.

5.答案：B

解析：如图，连接OE，OF，则.是等边三角形，.在四边形BEOF中，，.

6.答案：A

解析：当时,,解(舍去)；当时,,解得;当时，,方程没有实数解;当时,,方程没有实数解.所以方程的解为0或.故选A.

7.答案：A

解析：与的边AB相切，

，

，

连接，如图，

绕点B按顺时针方向旋转得到，

，，，

，

为等边三角形，

，

，

.

故选：A.

8.答案：D

解析：过点A作，交BC于点F.

在等边中，，，

.

在中，

，

，

故选：D.

9.答案：C

解析：二次函数图象的对称轴为直线，①若，则当时，函数取得最大值，此时，，解得，不合题意，舍去；②若，则当时，函数取得最大值，此时，解得，不满足，；③若，则当时，函数取得最大值，此时，，解得.综上，当或时，二次函数有最大值4.故选C.

10.答案：A

解析：如图，延长CO交于点E，连接ED，交AO于点M，此时周长最小.

设AB于相切于点F，连接OF，则.

.

.

.

且OC为的半径.

CD是的切线.

.

.

.

即：.

解得：.

.

的周长最小值为：.

故选：A.

11.答案：B

解析：如图，分别作与的平分线，交点为P.和都是等边三角形，AP与BP为CD、CE垂直平分线.圆心O是一个定点.连接OC.若半径OC最短，则.又，，，，在直角中，，，又，由勾股定理可知.故选B.

12.答案：C

解析：由图象可知，图像开口向下，，对称轴为，故，故，且，则故②正确.

图象与y轴的交点为正半轴，，则，故①错误，由图象可知当时，函数取最大值，将，代入，中得：，由图象可知函数与x轴交点为，对称轴为，将，故函数图象与x轴的另一交点为，设函数解析式为：，将交点坐标代入得：，故化简得：，将，代入可得：，故函数的最大值为-4a，故③正确，变形为：要使方程无实数根，则，将，，代入得：，因为，则，则，综上所述，故④正确，则②③④正确，故选C.

13.答案：76°

解析：四边形ABCD是的内接四边形，.，，.

14.答案：3

解析：设，

则原方程化为：，

去括号移项得：，

，

解得，，

，

.

故答案为：3.

15.答案：

解析：根据题意列表如下，可知共有9种等可能的结果，其中两张卡片上的字母相同的结果有3种，故所求概率为.

16.答案：

解析：因为，所以将抛物线绕它的顶点旋转180°后，所得抛物线的表达式为.

17.答案：③④⑤

解析：①当时，y随x增大而减小，

抛物线顶点D的横坐标为1，

对称轴为直线，

抛物线开口向下，

当时，y随x增大而增大，

不正确；

②，

，，

，

，

不正确；

③，

时，，，

，

，

，

正确；

④，

，，

，

，

正确；

⑤当时，，

抛物线与x轴交于A、B两点，其中点B坐标为，对称轴为直线，

，

设抛物线解析式为，

当时，，

正确.

故答案为，③④⑤.

18.答案：

解析：设的所在圆的圆心为O，连接CO，并延长交于D，连接AO、BO、AD、BD，如图，

，，

，

四边形ACBD是的内接四边形，

，

，

，

CD是的直径，

，

，

，

，

由勾股定理得：，

的半径为，

的长度是，

故答案为：.

19.答案：(1)见解析

(2)见解析

(3)4

解析：(1)和关于原点O成中心对称，

A，B，C三点的坐标依次为，，，

、、三点的坐标依次为，，

即为所求作；

(2)绕点顺时针旋转90°得到，

A，B，C三点的坐标依次为，，，

、、三点的坐标依次为，，，

即为所求作；

(3).

20.答案：(1)

(2)不存在，理由见解析

解析：(1)根据题意得，

解得.

(2)不存在.

，，

而和互为相反数，

，解得，

.

不存在实数k，使得和互为相反数.

21.答案：(1)

(2)P的坐标为

解析：(1)将，代入得：

，

解得：，

这个函数的解析式为：；

把代入得，，

y的取值范围是.

(2)点在该函数的图象上，

，

，

，

解得，，

点P的坐标为.

22.答案：(1)600；

(2)这种服装销售单价确定为80元为宜，这时应进400件服装

(3)定价为75元时，可获得最大利润，最大利润是12500元

解析：(1)提价10元，则销售量为件；

提价x元，则销售量为件；

故答案为：600；

(2)设这种服装提价x元，

由题意得：，

解这个方程得：，

当时，，舍去；

当时，，

当时，，，

答：这种服装销售单价确定为80元为宜，这时应进400件服装；

(3)设利润为y元，根据题意得：

，

当，定价为元时，可获得最大利润，最大利润为12500元.

23.答案：（1）证明：连接CO.

PC是的切线，

，即，

.

AB是的直径，

，

，

.

，

，

，即.

（2）解：的大小不发生变化.

，，，，

.

24.答案：（1）见解析

（2）这个游戏公平，理由见解析

解析：（1）方法一：列表如下.

由上表可知所有可能出现的结果共有8种.
方法二：画树状图如图所示.

开始由树状图可知所有可能出现的结果共有8种.
（2）这个游戏公平.
理由：由树状图或表格可知，共有8种等可能的结果，
其中为奇数的结果有4种：，，，，
故P（演奏（月光下的凤尾竹）=，P（演奏《彩云之南》）.
故这个游戏公平.

25.答案：（1）见解析

（2）见解析

（3）的面积

解析：（1）证明：如图，连接OC.

AB是的直径，

，

，

，

.

，

.

，

，

，

，

CD是的切线.

（2）证明：，，，

，

.

又，

.

（3），，

，

BC是斜边上的中线，

，

.

在中，由勾股定理得.

的面积.

26.答案：(1)

(2)D的坐标为：，

(3)点Q的坐标为，

解析：(1)设抛物线的解析式为，

抛物线的对称轴为，

，

，

抛物线经过，与y轴交于点，

，

，，，

此抛物线的解析式为；

(2)D为抛物线上一点，且，

，

，

，

，

①当时，根据题意得：，

解得：，，

C点坐标为，点D不与点C重合，

点D坐标为；

②当时，根据题意得：，

解得：，

点D坐标为；

(3)解：抛物线经过，，

令，则，

解得：，，

点B的坐标为，

设对称轴与x轴相交于点E，过点Q作对称轴于点F，

，

是等腰直角三角形，

，，

，

，

，

在和中，

，

，

，，

设，则

①若点Q在x轴上方时，则点Q的坐标为，

点Q为抛物线上一点，

，

整理得：

解得：，舍)，

点Q的坐标为；

②若点Q在轴下方时，则点Q的坐标为，

点Q为抛物线上一点，

，

整理得：，

解得：，舍)，

点Q的坐标为，

综上所述，点Q的坐标为，