专题04 与角度、面积等相关的动态问题-八年级数学秘籍之三角形全等、轴对称及几何动态问题思维训练

这是一份专题04 与角度、面积等相关的动态问题-八年级数学秘籍之三角形全等、轴对称及几何动态问题思维训练，文件包含专题04与角度面积等相关的动态问题解析版docx、专题04与角度面积等相关的动态问题原卷版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
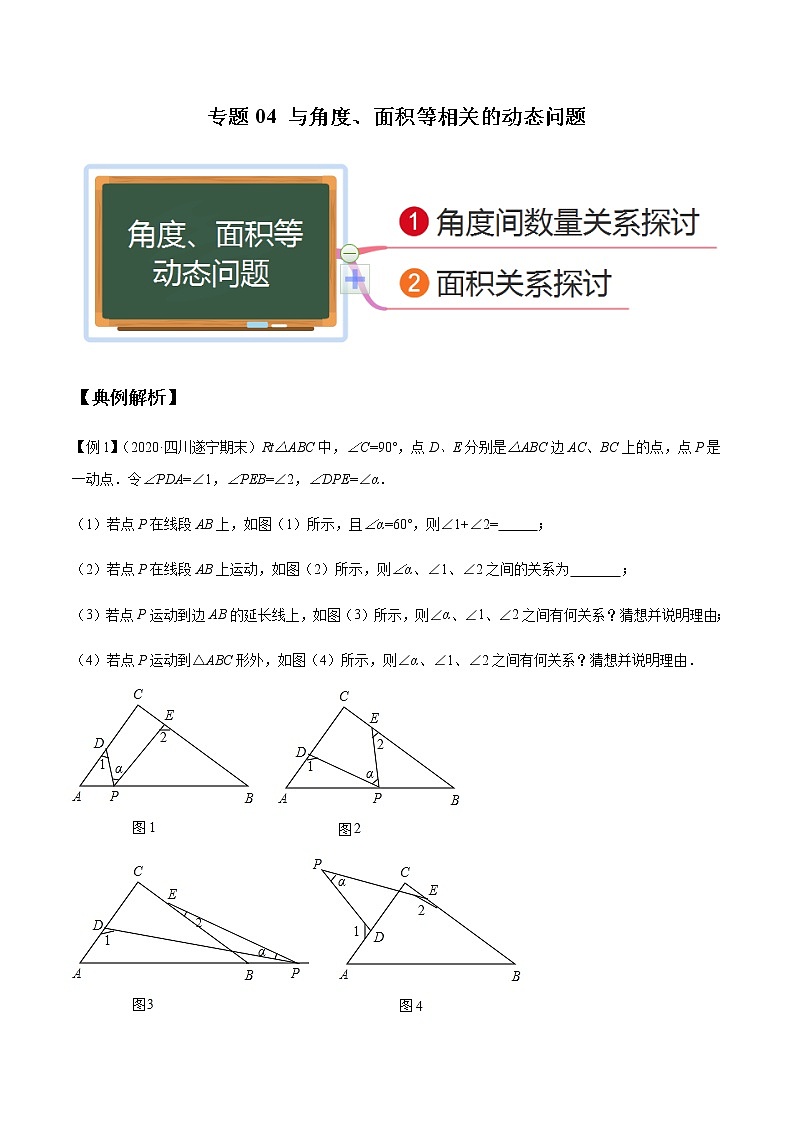
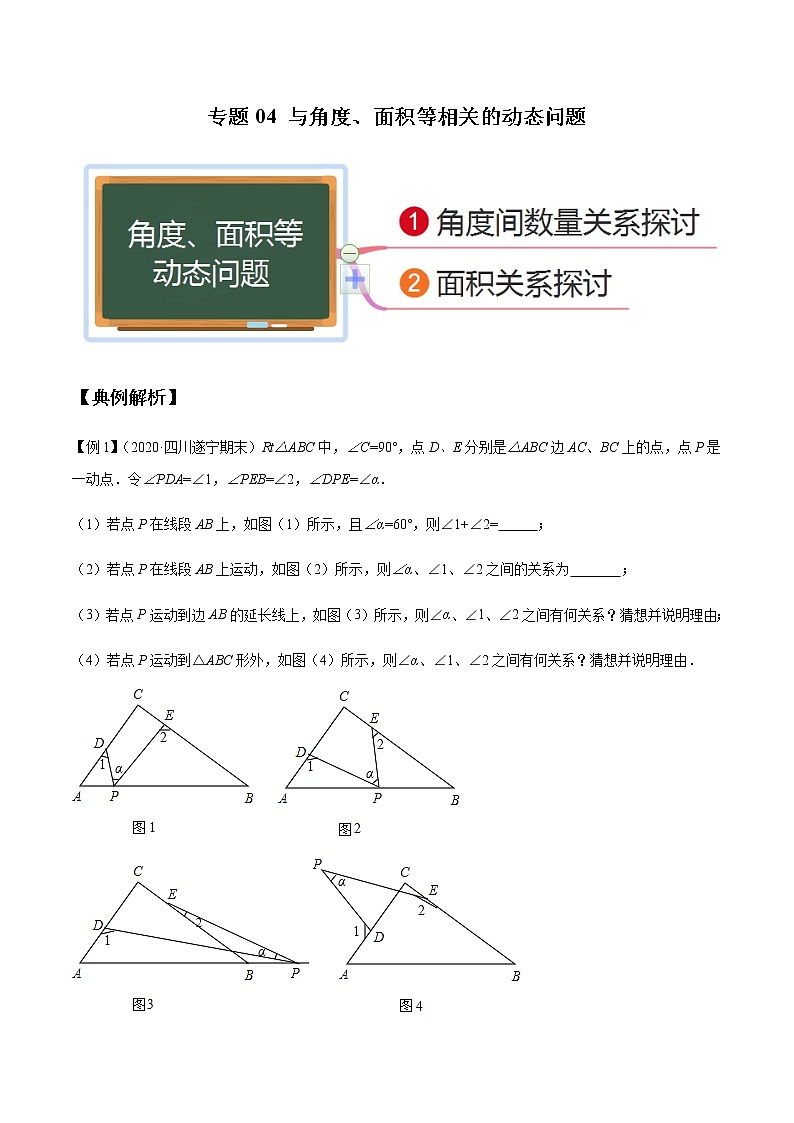
专题04 与角度、面积等相关的动态问题【典例解析】【例1】（2020·四川遂宁期末）Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）若点P在线段AB上，如图（1）所示，且∠α=60°，则∠1+∠2=       ；（2）若点P在线段AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为         ；（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由；（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由．     【变式1-1】（2020·福建龙岩期中）将一副三角板中的两块直角三角尺的直角顶点按如图所示的方式叠放在一起（其中，，），固定三角板，另一三角板的边从边开始绕点顺时针旋转，设旋转的角度为．    （1）当时； ①若，则的度数为        ；②若，求的度数；（2）由（1）猜想与的数量关系，并说明理由；（3）当时，这两块三角尺是否存在一组边互相垂直？若存在，请直接写出所有可能的值，并指出哪两边互相垂直（不必说明理由）；若不存在，请说明理由．   【变式1-2】（2019·上海市市期中）结合“爱市西，爱生活，会创新”的主题，某同学设计了一款“地面霓虹探测灯”，增加美观的同时也为行人的夜间行路带去了方便．他的构想如下：在平面内，如图1所示，灯射线从开始顺时针旋转至便立即回转，灯射线从开始顺时针旋转至便立即回转，两灯不停交叉照射巡视．若灯转动的速度是每秒2度，灯转动的速度是每秒1度．假定主道路是平行的，即，且．（1）填空：______；（2）若灯射线先转动60秒，灯射线才开始转动，在灯射线到达之前，灯转动几秒，两灯的光束互相平行？（3）如图2，若两灯同时转动，在灯射线到达之前，若射出的光束交于点，过作交于点，且，则在转动过程中，请探究与的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由． 【例2】（2020·湖北广水期末）如图，以直角三角形AOC的直角顶点O为原点，以OC，OA所在直线为轴和轴建立平面直角坐标系，点A（0，a），C（b，0）满足．（1）a=        ；b=       ；直角三角形AOC的面积为         ．（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发以每秒2个单位长度的速度向点O匀速移动，Q点从O点出发以每秒1个单位长度的速度向点A匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠DCO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOD，∠OHC，∠ACE之间的数量关系，并证明你的结论(三角形的内角和为180)． 【变式2-1】（2020·山东日照期末）如图，在平面直角坐标系中，已知△ABC，点A的坐标是（3，0），点B的坐标是（a，b），且点C在x轴的负半轴上，且AC＝5．（1）直接写出点B、C的坐标；（2）在坐标轴上是否存在点P，使若存在，求出点P的坐标；若不存在，请说明理由；（3）把点C往上平移3个单位得到点H，作射线CH，连接BH，点M在射线CH上运动（不与点C、H重合），试探究∠HBM，∠BMA，∠MAC之间的数量关系，并证明你的结论． 【习题专练】1. （2020·长沙市月考）在平面直角坐标系中，点O为原点，点B（0，﹣4）是y轴负半轴上一点，将点B向右平移6个单位得到点A（6，﹣4）．（1）如图1，动点P从点B出发，以每秒2个单位长度的速度沿BA方向运动，同时动点Q从点O出发，以每秒3个单位长度的速度沿y轴向上运动，当点P运动到点A时，P、Q同时停止运动，设点P运动时间为t秒．①用含t的式子表示P，Q两点的坐标．②是否存在t使△BPQ的面积为4t＋12？若存在，求出t，并写出此时点P、Q的坐标；若不存在，说明理由．（2）如图2，点D为线段OA（端点除外）上某一点，当点D在线段上运动时，过点D作直线EF交x轴正半轴于E，交直线AB于F，∠EOD，∠AFD的平分线相交于点N，若∠ODF＝α，请用含α的式子表示∠ONF的大小，并说明理由． 2.（2019·湖北武昌期中）如图，平面直角坐标系中，轴，点从原点出发在轴上以单位/秒的速度向轴的正方向运动，运动的时间为秒．平分． (提示：中，，若则，反之亦然) （1）当时，        ；（2）当的面积为3时，求A点运动的时间t；（3）当时，求的度数(用含的式子表示，且不含绝对值)． 3.（2019·北京市期末）如图，在直角三角形中，，．点是直线上一个动点(点不与点，重合)，连接，在线段的延长线上取一点，使得．过点作，交直线于点．（1）如图1，当点在线段上时，若，则_________；（2）当点在线段的延长线上时，在图2中依题意补全图形，并判断与有怎样的数量关系，写出你的结论，并证明；（3）在点运动的过程中，直接写出与的数量关系为_________．   4.（2019·湖北黄石期中）如图：已知在平面直角坐标系中点A（a，b）点B（a，0），且满足|2a-b|+（b-4）2=0．（1）求点A、点B的坐标；（2）已知点C（0，b），点P从B点出发沿x轴负方向以1个单位每秒的速度移动，同时点Q从C点出发，沿y轴负方向以2个单位每秒的速度移动，t=3时，AQ交x轴于M，作∠ACO，∠AMB的角平分线交于点N，判断是否为定值，若是定值求其值；若不是定值，说明理由．   5.（2020·商城县月考）如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t=___________________，△APE的面积等于6．