专题08 互补型旋转模型-八年级数学上册全等三角形基本模型探究（人教版）

专题08 互补型旋转模型

【模型说明】

【例题精讲】

例1．（基本模型）如图，在四边形中，于，则的长为__________

【答案】

【详解】解：过点B作交DC的延长线交于点F，如右图所示，

∵，，

，

，∴≌

， ，

，即，，

故答案为．

例2．（模型探究）回答问题

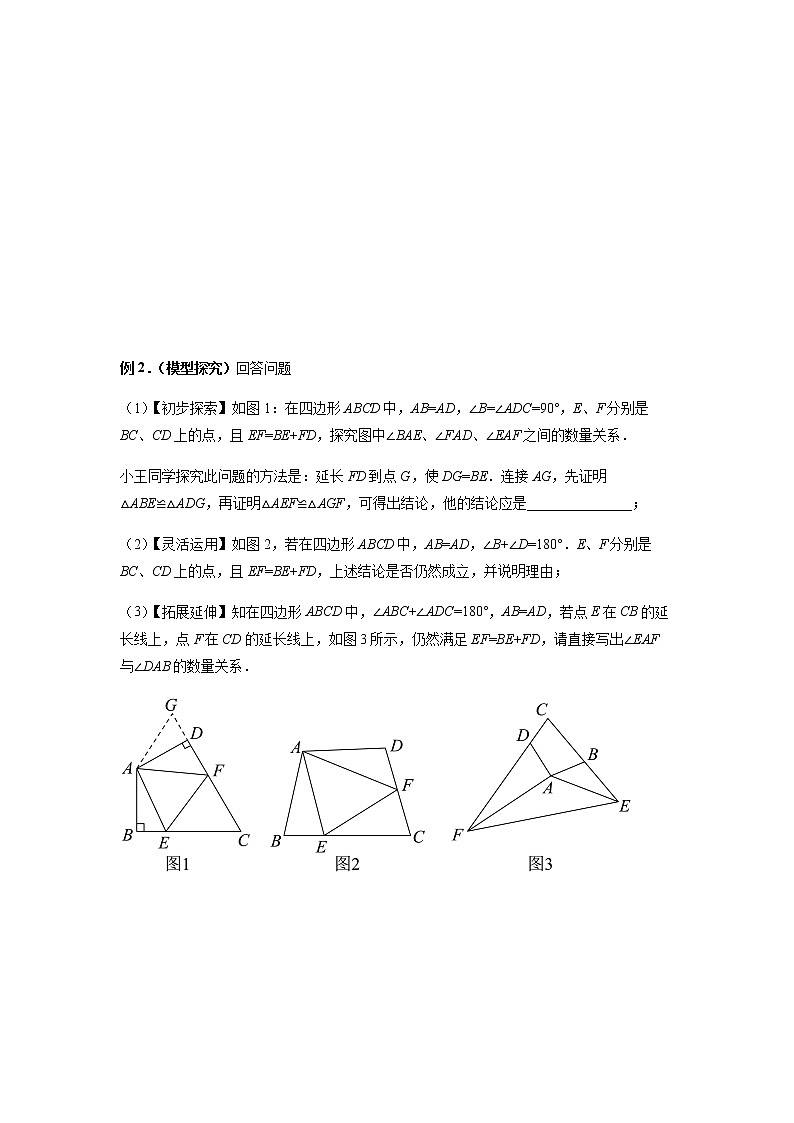
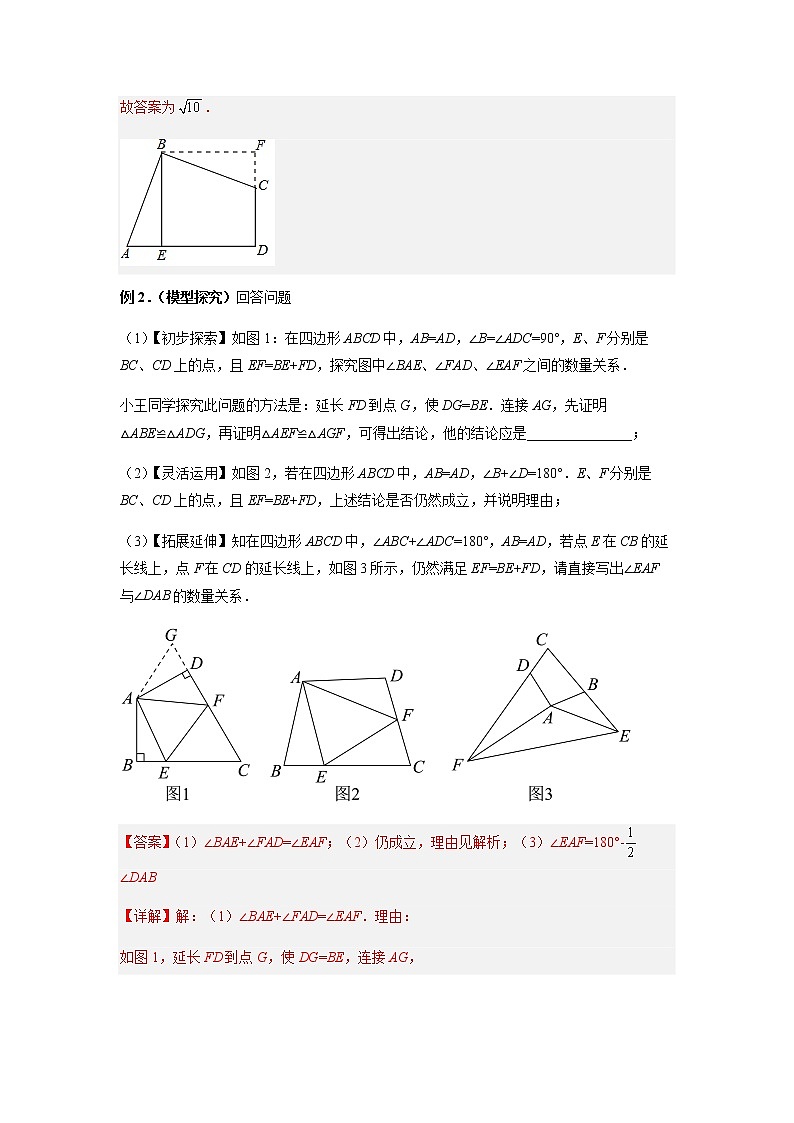
（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．

小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是_______________；

（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；

（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．

【答案】（1）∠BAE+∠FAD=∠EAF；（2）仍成立，理由见解析；（3）∠EAF=180°-∠DAB

【详解】解：（1）∠BAE+∠FAD=∠EAF．理由：

如图1，延长FD到点G，使DG=BE，连接AG，

∵∠B=∠ADF=90°，∠ADG=∠ADF=90°，

∴∠B=∠ADG=90°，

又∵AB=AD，

∴△ABE≌△ADG（SAS），

∴∠BAE=∠DAG，AE=AG，

∵EF=BE+FD=DG+FD=GF，AF=AF，

∴△AEF≌△AGF（SSS），

∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；

故答案为：∠BAE+∠FAD=∠EAF；

（2）仍成立，理由：

如图2，延长FD到点G，使DG=BE，连接AG，

∵∠B+∠ADF=180°，∠ADG+∠ADF=180°，

∴∠B=∠ADG，

又∵AB=AD，

∴△ABE≌△ADG（SAS），

∴∠BAE=∠DAG，AE=AG，

∵EF=BE+FD=DG+FD=GF，AF=AF，

∴△AEF≌△AGF（SSS），

∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF；

（3）∠EAF=180°-∠DAB．

证明：如图3，在DC延长线上取一点G，使得DG=BE，连接AG，

∵∠ABC+∠ADC=180°，∠ABC+∠ABE=180°，

∴∠ADC=∠ABE，

又∵AB=AD，

∴△ADG≌△ABE（SAS），

∴AG=AE，∠DAG=∠BAE，

∵EF=BE+FD=DG+FD=GF，AF=AF，

∴△AEF≌△AGF（SSS），

∴∠FAE=∠FAG，

∵∠FAE+∠FAG+∠GAE=360°，

∴2∠FAE+（∠GAB+∠BAE）=360°，

∴2∠FAE+（∠GAB+∠DAG）=360°，

即2∠FAE+∠DAB=360°，

∴∠EAF=180°-∠DAB．

例3．（培优综合）如图，在中，，，点在上，点在上，，连接，，，垂足为．证明：．

【答案】见解析

【详解】证明：如图，延长到点，使，连接、，

，，

，，

，，

，，，

，

，，，，

，，．

【课后作业】

1．将4个边长都是2的正方形按如图所示的样子摆放，点，，分别是三个正方形的中心，则图中三块重叠部分的面积的和为（    ）.

A．2 B．3 C．6 D．8

【答案】B

【详解】解：如图，

连接AP，AN，点A是正方形的对角线的交点，

则，，

，

，

≌，

四边形AENF的面积等于的面积，

而的面积是正方形的面积的，而正方形的面积为4，

四边形AENF的面积为，三块阴影面积的和为．

故选B．

2．Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论

①(BE+CF)=BC，②，③AD·EF，④AD≥EF，⑤AD与EF可能互相平分，其中正确结论的个数是【   】

A．1个 B．2个 C．3个 D．4个

【答案】C

【详解】解:∵Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，

∴AD =DC，∠EAD=∠C=45°，∠EDA=∠MDN－∠ADN =90°－∠ADN=∠FDC．

∴△EDA≌△FDC（ASA）．

∴AE=CF．

∴BE+CF= BE+ AE=AB．

在Rt△ABC中，根据勾股定理，得AB=BC．

∴(BE+CF)=BC．

∴结论①正确．

设AB=AC=a，AE=b，则AF=BE= a－b．

∴．

∴．

∴结论②正确．

如图，过点E作EI⊥AD于点I，过点F作FG⊥AD于点G，过点F作FH⊥BC于点H，ADEF相交于点O．

∵四边形GDHF是矩形，△AEI和△AGF是等腰直角三角形，

∴EO≥EI（EF⊥AD时取等于）=FH=GD，

OF≥GH（EF⊥AD时取等于）=AG．

∴EF=EO＋OF≥GD＋AG=AD．

∴结论④错误．

∵△EDA≌△FDC，

∴．

∴结论③错误．

又当EF是Rt△ABC中位线时，根据三角形中位线定理知AD与EF互相平分．

∴结论⑤正确．

综上所述，结论①②⑤正确．故选C．

3．如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．

【答案】

【详解】解：

将△OBC绕O点旋转90°，

∵OB=OA

∴点B落在A处，点C落在D处

且有OD=OC=3，∠COD=90°，∠OAD=∠OBC，

在四边形OACB中

∵∠BOA=∠BCA=90°，

∴∠OBC+∠OAC=180°，

∴∠OAD+∠OAC=180°

∴C、A、D三点在同一条直线上，

∴△OCD为等要直角三角形，根据勾股定理

CD2=OC2+OD2

即CD2=32+32=18，解得CD= ，即BC+AC=.

4．如图，P是等边三角形ABC内一点，将线段BP绕点B逆时针旋转60°得到线段BQ，连接AQ．若PA=4，PB=5，PC=3，则四边形APBQ的面积为_______．

【答案】

【详解】解：连接PQ，

由旋转的性质可得，BP=BQ，

又∵∠PBQ=60°，

∴△BPQ是等边三角形，

∴PQ=BP，

在等边三角形ABC中，∠CBA=60°，AB=BC，

∴∠ABQ=60°-∠ABP

∠CBP=60°-∠ABP

∴∠ABQ=∠CBP

在△ABQ与△CBP中

，

∴△ABQ≌△CBP(SAS)，∴AQ=PC，

又∵PA=4，PB=5，PC=3，

∴PQ=BP=5，PC=AQ=3，

在△APQ中，因为，25=16+9，

∴由勾股定理的逆定理可知△APQ是直角三角形，

∴，故答案为：

5．问题背景：如图1，在四边形中，，，，，，绕B点旋转，它的两边分别交、于E、F．探究图中线段，，之间的数量关系．小李同学探究此问题的方法是：延长到G，使，连接，先证明，再证明，可得出结论，他的结论就是_______________；

探究延伸1：如图2，在四边形中，，，，，绕B点旋转，它的两边分别交、于E、F．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由．

探究延伸2：如图3，在四边形中，，，，绕B点旋转，它的两边分别交、于E、F．上述结论是否仍然成立？并说明理由．

实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西的A处舰艇乙在指挥中心南偏东的B处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处，且指挥中心观测两舰艇视线之间的夹角为，试求此时两舰艇之间的距离．

【答案】EF=AE+CF．探究延伸1：结论EF=AE+CF成立．探究延伸2：结论EF=AE+CF仍然成立．实际应用：210海里．

【详解】解：EF=AE+CF

理由：延长到G，使，连接，

在△BCG和△BAE中，

，

∴（SAS），∴BG=BE，∠CBG=∠ABE，

∵∠ABC=120°，∠MBN=60°，∴∠ABE+∠CBF=60°，

∴∠CBG+∠CBF=60°，即∠GBF=60°，

在△BGF和△BEF中，

，

∴△BGF≌△BEF（SAS），∴GF=EF，

∵GF=CG+CF=AE+CF，∴EF=AE+CF．

探究延伸1：结论EF=AE+CF成立．

理由：延长到G，使，连接，

在△BCG和△BAE中，

，

∴（SAS），∴BG=BE，∠CBG=∠ABE，

∵∠ABC=2∠MBN，∴∠ABE+∠CBF=∠ABC，∴∠CBG+∠CBF=∠ABC，

即∠GBF=∠ABC，

在△BGF和△BEF中，

，

∴△BGF≌△BEF（SAS），∴GF=EF，

∵GF=CG+CF=AE+CF，∴EF=AE+CF．

探究延伸2：结论EF=AE+CF仍然成立．

理由：延长到G，使，连接，

∵，∠BCG+∠BCD=180°，

∴∠BCG=∠BAD

在△BCG和△BAE中，

，

∴（SAS），

∴BG=BE，∠CBG=∠ABE，

∵∠ABC=2∠MBN，

∴∠ABE+∠CBF=∠ABC，

∴∠CBG+∠CBF=∠ABC，

即∠GBF=∠ABC，

在△BGF和△BEF中，

，

∴△BGF≌△BEF（SAS），∴GF=EF，

∵GF=CG+CF=AE+CF，∴EF=AE+CF．

实际应用：连接EF，延长AE，BF相交于点C，

∵∠AOB=30°+90°+(90°-70°)=140°，∠EOF=70°，

∴∠EOF=∠AOB

∵OA=OB，∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°，

∴符合探索延伸中的条件

∴结论EF= AE+CF仍然成立

即EF=75×1.2+100×1.2=210（海里）

答：此时两舰艇之间的距离为210海里．

6．五边形ABCDE中，，，，求证：AD平分∠CDE．

【答案】见解析

【详解】延长DE至F，使得，连接AC.

∵，，

∴

∵，，

∴△ABC≌△AEF．

∴，

∵，

∴，

∴△ADC≌△ADF，∴

即AD平分∠CDE．

7．如图，△ABC是边长为4的等边三角形，点D是线段BC的中点，∠EDF=120°，把∠EDF绕点D旋转，使∠EDF的两边分别与线段AB、AC交于点E、F．

（1）当DF⊥AC时，求证：BE=CF；

（2）在旋转过程中，BE+CF是否为定值？若是，求出这个定值；若不是，请说明理由

【答案】（1）证明见解析；（2）是，2.

【详解】（1）∵△ABC是边长为4的等边三角形，点D是线段BC的中点，

∴∠B=∠C=60°，BD=CD，

∵DF⊥AC，

∴∠DFA=90°，

∵∠A+∠EDF+∠AFD+∠AED=180°，

∴∠AED=90°，

∴∠DEB=∠DFC，且∠B=∠C=60°，BD=DC，

∴△BDE≌△CDF（AAS）

（2）过点D作DM⊥AB于M，作DN⊥AC于N，

则有∠AMD=∠BMD=∠AND=∠CND=90°．

∵∠A=60°，

∴∠MDN=360°-60°-90°-90°=120°．

∵∠EDF=120°，∴∠MDE=∠NDF．

在△MBD和△NCD中，

，

∴△MBD≌△NCD（AAS），BM=CN，DM=DN．

在△EMD和△FND中，

，

∴△EMD≌△FND（ASA），∴EM=FN，

∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN

=2BM=2BD×cos60°=BD=BC=2.

8．如图所示，中，，，把一块含角的直角三角板的直角顶点放在的中点上（直角三角板的短直角边为，长直角边为），将三角板绕点按逆时针方向旋转.

（1）在如图所见中，交于，交于，证明；

（2）继续旋转至如图所见，延长交于，延长交于，证明.

【答案】(1)见解析；（2）见解析.

【详解】证明：（1）连接BD,

∵AB=BC，∠ABC=90°，点D为AC的中点

∴BD⊥AC，∠A=∠C=45°，∴BD=AD=CD

∴∠ABD=∠A=45°，∴∠MBD=∠C=45°

∵∠MDB+∠BDN=90°，∠NDC+∠BDN=90°

∴∠MDB=∠NDC

在△MDB和△NDC中

∴△MDB≌△NDC（ASA）

∴DM=DN（5分）

（2）DM=DN仍然成立．理由如下：连接BD，

由（1）知BD⊥AC，BD=CD，∴∠ABD=∠ACB=45°

∵∠ABD+∠MBD=180°∠ACB+∠NCD=180° ，∴∠MBD=∠NCD

∵BD⊥AC，∴∠MDB+∠MDC=90°

又∠NDC+∠MDC=90°，∴∠MDB=∠NDC

在△MDB和△NDC中

∴△MDB≌△NDC（ASA） 

∴DM=DN.

9．问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．

【类比引申】如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足                      关系时，仍有EF=BE+FD．

【探究应用】如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：=1.41，=1.73）

【答案】【发现证明】证明见解析；【类比引申】∠BAD=2∠EAF；【探究应用】109．2米．

【分析】【发现证明】根据旋转的性质可以得到△ADG≌△ABE，则GF=BE+DF，只要再证明△AFG≌△AFE即可．

【类比引申】延长CB至M，使BM=DF，连接AM，证△ADF≌△ABM，证△FAE≌△MAE，即可得出答案；

【探究应用】利用等边三角形的判定与性质得到△ABE是等边三角形，则BE=AB=80米．把△ABE绕点A逆时针旋转150°至△ADG，根据旋转的性质可以得到△ADG≌△ABE，则GF=BE+DF，只要再证明△AFG≌△AFE即可得出EF=BE+FD．

【详解】解：如图（1），

∵△ADG≌△ABE，

∴AG=AE，∠DAG=∠BAE，DG=BE，

又∵∠EAF=45°，即∠DAF+∠BEA=∠EAF=45°，

∴∠GAF=∠FAE，

在△GAF和△FAE中，

AG=AE，∠GAF=∠FAE，AF=AF，

∴△AFG≌△AFE（SAS）．

∴GF=EF．

又∵DG=BE，

∴GF=BE+DF，

∴BE+DF=EF．

【类比引申】∠BAD=2∠EAF．

理由如下：如图（2），延长CB至M，使BM=DF，连接AM，

∵∠ABC+∠D=180°，∠ABC+∠ABM=180°，

∴∠D=∠ABM，

在△ABM和△ADF中，

AB=AD，∠ABM=∠D，BM=DF，

∴△ABM≌△ADF（SAS），

∴AF=AM，∠DAF=∠BAM，

∵∠BAD=2∠EAF，

∴∠DAF+∠BAE=∠EAF，

∴∠EAB+∠BAM=∠EAM=∠EAF，

在△FAE和△MAE中，

AE=AE，∠FAE=∠MAE，AF=AM，

∴△FAE≌△MAE（SAS），

∴EF=EM=BE+BM=BE+DF，

即EF=BE+DF．

故答案是：∠BAD=2∠EAF．

【探究应用】如图3，把△ABE绕点A逆时针旋转150°至△ADG，连接AF．

∵∠BAD=150°，∠DAE=90°，

∴∠BAE=60°．

又∵∠B=60°，

∴△ABE是等边三角形，

∴BE=AB=80米．

根据旋转的性质得到：∠ADG=∠B=60°，

又∵∠ADF=120°，

∴∠GDF=180°，即点G在CD的延长线上．

易得，△ADG≌△ABE，

∴AG=AE，∠DAG=∠BAE，DG=BE，

又∵∠EAG=∠BAD=150°，

∴∠GAF=∠FAE，

在△GAF和△FAE中，

AG=AE，∠GAF=∠FAE，AF=AF，

∴△AFG≌△AFE（SAS）．

∴GF=EF．

又∵DG=BE，

∴GF=BE+DF，

∴EF=BE+DF=80+40（﹣1）≈109.2（米），即这条道路EF的长约为109.2米．