初中数学北师大版八年级上册第七章 平行线的证明1 为什么要证明课堂检测

课  时  练

第7单元  平行线的证明

1 为什么要证明

一、填空题

1．小红前五次数学单元测试都是优秀，第六次单元测试也一定是优秀，这个判断是______的．(选填“正确”或“错误”)

2．要判断两条线段是否平行，仅靠观察是______的．(选填“行”或“不行”)

3．在一次1 500米的比赛中，有如下的判断：甲说：“丙第一，我第三．”乙说：“我第一，丁第四．”丙说：“丁第二，我第三．”结果是每人的两句话中都只说对了一句，则可判断第一名是______．

4．下列图案均由边长为单位长1个度的小正方形按一定规律拼接而成，依此规律，第五个图案中小正方形的个数为______．

二、选择题

5．下列结论你能肯定的是（     ）

A．今天下雨，明天一定不下雨

B．三个连续整数的积一定能被6整除

C．小明在数学竞赛中一定能获奖

D．两张相片看起来不一样，则肯定照的不是同一个人

6．下列问题用到推理的是（    ）

A．根据x＝1，y＝1，得x＝y

B．观察得到的四边形有四个内角

C．老师告诉了我们关于金字塔的许多奥秘

D．由公理知道过两点有且只有一条直线

7．下列推理正确的是（    ）

A．如果a＞b，b＞c，则a＞c

B．若a＞b，则ac＞bc

C．若∠AOB＝∠BOC，则这两个角是对顶角

D．如果两角的和等于180°，那么这两个角互为邻补角

8．甲、乙、丙三位先生是同一家公司的职员，他们的夫人M，N，P也都是这家公司的职员，知情者介绍说：“M的丈夫是乙的好友，并在三位先生中最年轻；丙的年龄比P的丈夫大．”根据该知情者提供的信息，我们可以推出三对夫妇分别是(     )

A．甲—M，乙—N，丙—P        B．甲—M，乙—P，丙—N

C．甲—N，乙—P，丙—M        D．甲—P，乙—N，丙—M

三、解答题

9．(1)我们知道：2×2＝4，2＋2＝4.试问：对于任意数a与b，是否一定有结论a×b＝a＋b?

(2)有人认为，对于所有自然数n，代数式n2－n＋11的值都是质数，你怎么看待这个结论？

10.某公园计划砌一个形状如图1所示的喷水池，后有人建议改为图2所示的形状，且外圆直径不变，喷水池边缘的宽度、高度不变，你认为哪一种需要的材料多(即哪个周长更长)？并说明理由．

B组(中档题)

四、填空题

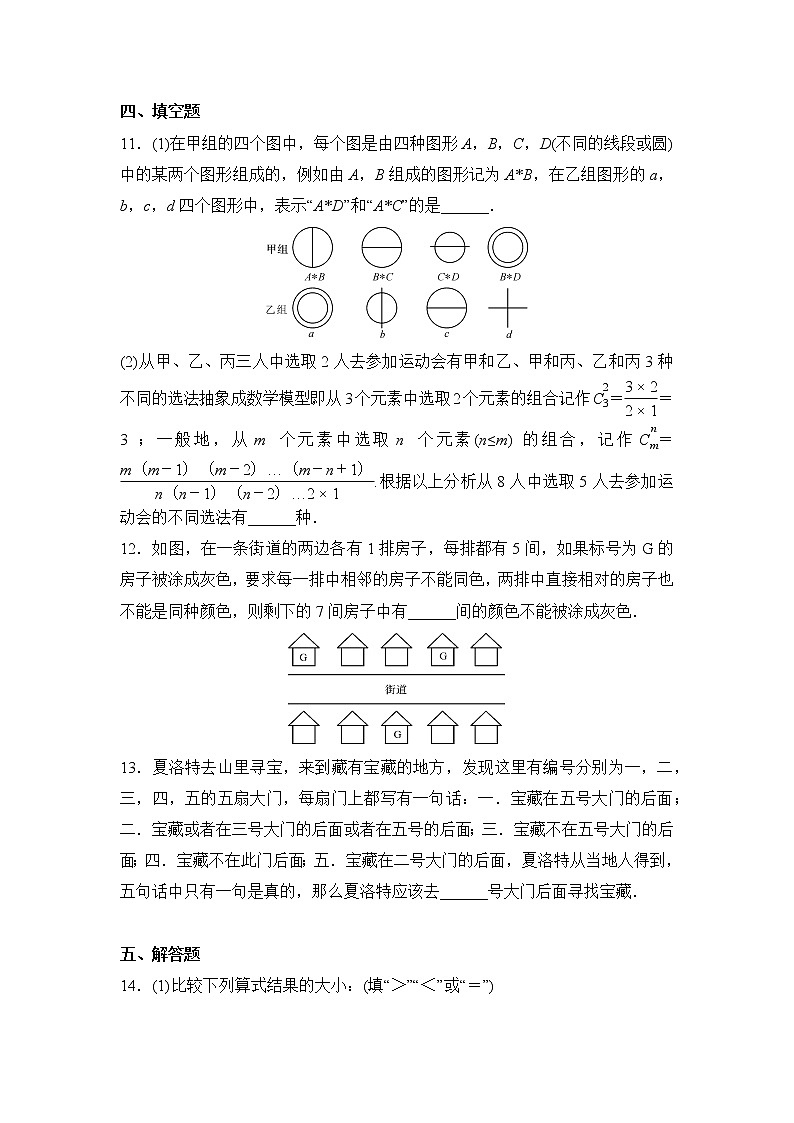
11．(1)在甲组的四个图中，每个图是由四种图形A，B，C，D(不同的线段或圆)中的某两个图形组成的，例如由A，B组成的图形记为A*B，在乙组图形的a，b，c，d四个图形中，表示“A*D”和“A*C”的是______．

(2)从甲、乙、丙三人中选取2人去参加运动会有甲和乙、甲和丙、乙和丙3种不同的选法．抽象成数学模型，即从3个元素中选取2个元素的组合，记作C＝＝3；一般地，从m个元素中选取n个元素(n≤m)的组合，记作C＝.根据以上分析从8人中选取5人去参加运动会的不同选法有______种．

12．如图，在一条街道的两边各有1排房子，每排都有5间，如果标号为G的房子被涂成灰色，要求每一排中相邻的房子不能同色，两排中直接相对的房子也不能是同种颜色，则剩下的7间房子中有______间的颜色不能被涂成灰色．

13．夏洛特去山里寻宝，来到藏有宝藏的地方，发现这里有编号分别为一，二，三，四，五的五扇大门，每扇门上都写有一句话：一．宝藏在五号大门的后面；二．宝藏或者在三号大门的后面或者在五号的后面；三．宝藏不在五号大门的后面；四．宝藏不在此门后面；五．宝藏在二号大门的后面，夏洛特从当地人得到，五句话中只有一句是真的，那么夏洛特应该去______号大门后面寻找宝藏．

五、解答题

14．(1)比较下列算式结果的大小：(填“＞”“＜”或“＝”)

①42＋32______2×4×3；

②(－2)2＋12______2×(－2)×1；

③()2＋()2______2××；

④32＋32______2×3×3.

(2)通过观察、归纳，写出能反映这种规律的一般结论，并说明理由．

C组(综合题)

15．如图，已知∠EFC＋∠BDC＝180°，∠DEF＝∠B，试判断DE与BC的位置关系，并说明理由．

参考答案

A组(基础题)

一、填空题

1．小红前五次数学单元测试都是优秀，第六次单元测试也一定是优秀，这个判断是错误的．(选填“正确”或“错误”)

2．要判断两条线段是否平行，仅靠观察是不行的．(选填“行”或“不行”)

3．在一次1 500米的比赛中，有如下的判断：甲说：“丙第一，我第三．”乙说：“我第一，丁第四．”丙说：“丁第二，我第三．”结果是每人的两句话中都只说对了一句，则可判断第一名是乙．

4．下列图案均由边长为单位长1个度的小正方形按一定规律拼接而成，依此规律，第五个图案中小正方形的个数为41．

二、选择题

5．下列结论你能肯定的是（  B  ）

A．今天下雨，明天一定不下雨

B．三个连续整数的积一定能被6整除

C．小明在数学竞赛中一定能获奖

D．两张相片看起来不一样，则肯定照的不是同一个人

6．下列问题用到推理的是（  A  ）

A．根据x＝1，y＝1，得x＝y

B．观察得到的四边形有四个内角

C．老师告诉了我们关于金字塔的许多奥秘

D．由公理知道过两点有且只有一条直线

7．下列推理正确的是（  A  ）

A．如果a＞b，b＞c，则a＞c

B．若a＞b，则ac＞bc

C．若∠AOB＝∠BOC，则这两个角是对顶角

D．如果两角的和等于180°，那么这两个角互为邻补角

8．甲、乙、丙三位先生是同一家公司的职员，他们的夫人M，N，P也都是这家公司的职员，知情者介绍说：“M的丈夫是乙的好友，并在三位先生中最年轻；丙的年龄比P的丈夫大．”根据该知情者提供的信息，我们可以推出三对夫妇分别是(  B  )

A．甲—M，乙—N，丙—P                            B．甲—M，乙—P，丙—N

C．甲—N，乙—P，丙—M                             D．甲—P，乙—N，丙—M

三、解答题

9．(1)我们知道：2×2＝4，2＋2＝4.试问：对于任意数a与b，是否一定有结论a×b＝a＋b?

(2)有人认为，对于所有自然数n，代数式n2－n＋11的值都是质数，你怎么看待这个结论？

解：(1)∵3×2＝6，3＋2＝5，6≠5，

∴不是任意数a与b都有结论a×b＝a＋b.

(2)结论不成立．理由：取n＝11时，n2－n＋11＝112－11＋11＝112.∴n＝11时，n2－n＋11是合数．

10.某公园计划砌一个形状如图1所示的喷水池，后有人建议改为图2所示的形状，且外圆直径不变，喷水池边缘的宽度、高度不变，你认为哪一种需要的材料多(即哪个周长更长)？并说明理由．

解：图1和图2需要的材料一样多．理由如下：

设大圆的半径为R，利用圆的周长公式得到图1中两个圆的周长为4πR；

同样设图2中三个小圆的半径分别为r1，r2，r3，则三个小圆的周长为2π(r1＋r2＋r3)，

由于r1＋r2＋r3＝R，则三个小圆的周长＝2πR，

所以图2中所有圆的周长和为4πR，即两种方案需要的材料一样多．

B组(中档题)

四、填空题

11．(1)在甲组的四个图中，每个图是由四种图形A，B，C，D(不同的线段或圆)中的某两个图形组成的，例如由A，B组成的图形记为A*B，在乙组图形的a，b，c，d四个图形中，表示“A*D”和“A*C”的是b，d．

(2)从甲、乙、丙三人中选取2人去参加运动会有甲和乙、甲和丙、乙和丙3种不同的选法．抽象成数学模型，即从3个元素中选取2个元素的组合，记作C＝＝3；一般地，从m个元素中选取n个元素(n≤m)的组合，记作C＝.根据以上分析从8人中选取5人去参加运动会的不同选法有56种．

12．如图，在一条街道的两边各有1排房子，每排都有5间，如果标号为G的房子被涂成灰色，要求每一排中相邻的房子不能同色，两排中直接相对的房子也不能是同种颜色，则剩下的7间房子中有6间的颜色不能被涂成灰色．

13．夏洛特去山里寻宝，来到藏有宝藏的地方，发现这里有编号分别为一，二，三，四，五的五扇大门，每扇门上都写有一句话：一．宝藏在五号大门的后面；二．宝藏或者在三号大门的后面或者在五号的后面；三．宝藏不在五号大门的后面；四．宝藏不在此门后面；五．宝藏在二号大门的后面，夏洛特从当地人得到，五句话中只有一句是真的，那么夏洛特应该去四号大门后面寻找宝藏．

五、解答题

14．(1)比较下列算式结果的大小：(填“＞”“＜”或“＝”)

①42＋32＞2×4×3；

②(－2)2＋12＞2×(－2)×1；

③()2＋()2＞2××；

④32＋32＝2×3×3.

(2)通过观察、归纳，写出能反映这种规律的一般结论，并说明理由．

解：结论：a2＋b2≥2ab(当a＝b时，等号成立).

理由：∵(a－b)2≥0，

∴a2－2ab＋b2≥0，即a2＋b2≥2ab.

C组(综合题)

15．如图，已知∠EFC＋∠BDC＝180°，∠DEF＝∠B，试判断DE与BC的位置关系，并说明理由．

解：DE∥BC.

理由：∵∠EFC＋∠BDC＝180°，∠ADC＋∠BDC＝180°，

∴∠EFC＝∠ADC，

∴AD∥EF.

∴∠DEF＝∠ADE.

又∵∠DEF＝∠B，

∴∠B＝∠ADE.

∴DE∥BC.