数学青岛版5.5 三角形内角和定理课文内容课件ppt

这是一份数学青岛版5.5 三角形内角和定理课文内容课件ppt，共21页。PPT课件主要包含了做一做，读一读等内容，欢迎下载使用。
1．掌握三角形内角和定理的证明及其简单应用.2.初步掌握利用辅助线证明，体会思维实验和符号化的理性作用.3.通过一题多解，初步体会思维的多向性，引导学生的个性化发展.
如图,我们把∠A移到了∠1的位置,∠B移到了∠2的位置.就得到了三角形三个内角的和等于180°.根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.
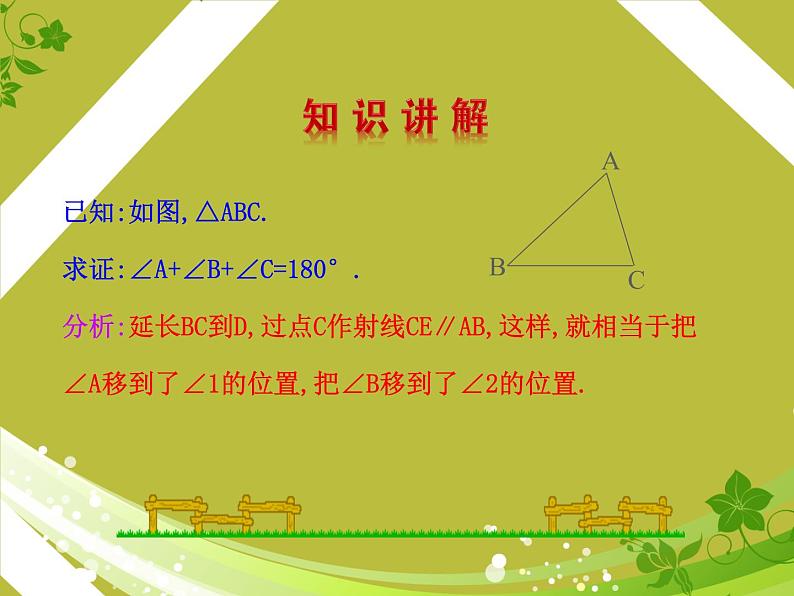
已知:如图,△ABC.求证:∠A+∠B+∠C=180°.分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
证明:作BC的延长线CD,过点C作射线CE∥AB,则∠1=∠A(两直线平行,内错角相等),∠2= ∠B(两直线平行,同位角相等).又∵∠1+∠2+∠3= 180° (平角的定义),∴∠A+∠B+∠ACB= 180° (等量代换).你还有其他方法来证明三角形内角和定理吗?
这里的CD,CE称为辅助线,辅助线通常画成虚线.
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗?请你帮小明把想法化为实际行动.证明:过点A作PQ∥BC,则 ∠1=∠B(两直线平行,内错角相等), ∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3= 180° (平角的定义),∴ ∠BAC+∠B+∠C= 180° (等量代换). 小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?
如图. ∠1是△ABC的一个外角, ∠1与图中的其他角有什么关系?∠1+∠4=180°；∠1>∠2；∠1>∠3；∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=180° (三角形内角和定理), ∠1+∠4=180° (平角的定义), ∴∠1= ∠2+∠3.(等量代换). ∴ ∠1>∠2,∠1>∠3(和大于部分).用文字表述为:三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.
在这里,我们通过三角形的内角和定理直接推导出两个新定理.像这样,由一个基本事实或定理直接推出的定理,叫做这个基本事实或定理的推论.推论可以当做定理使用.三角形内角和定理的推论:定理: 三角形的一个外角等于和它不相邻的两个内角的和.定理: 三角形的一个外角大于任何一个和它不相邻的内角.
在△ABC中: ∠1=∠2+∠3;所以∠1>∠2,∠1>∠3.这个结论以后可以直接运用.
例 已知:如图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.分析:要证明AD∥BC,只需要证明“同位角相等”或“内错角相等”或“同旁内角互补”.证明:∵∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),∠B=∠C (已知),∴∠C= ∠EAC(等式的性质).∵AD平分 ∠EAC(已知).∴∠DAC= ∠EAC(角平分线的定义).∴∠DAC=∠C(等量代换).∴AD∥BC(内错角相等,两直线平行).
例题是运用了定理“内错角相等,两直线平行”得到了证实.
已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.求证: ∠1>∠2.
证明:∵∠1是△ABC的一个外角(已知),∴∠1>∠3(三角形的一个外角大于任何一个和它不相邻的内角).∵∠3是△CDE的一个外角 (外角定义).∴∠3>∠2(三角形的一个外角大于任何一个和它不相邻的内角).∴∠1>∠2(不等式的性质).把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项转化为一种方法.
如果BC不动,把点A“拉离”BC,那么当点A越来越远离BC时,∠A就越来越小(越来越接近0°),而∠B和∠C则越来越大,它们的和越来越接近180°, 当把点A拉到无穷远时,便有AB∥AC,∠B和∠C成为同旁内角,它们的和等于180°.由此你能想到什么?
在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近180°),而∠B和∠C越来越小(越来越接近0°).由此你能想到什么?
1.如图所示，在△ABC中，CD是∠ACB的平分线，∠A=80°，∠B=60°，那么∠BDC=( )A.80° B.90°C.100° D.110°
2.若一个三角形三个内角度数的比为2∶3∶4，那么这个三角形是( )A.直角三角形 B.锐角三角形C.钝角三角形 D.等边三角形【解析】选B.由题意可设这个三角形的三个内角度数分别为2x,3x,4x,根据三角形内角和定理可得:2x+3x+4x＝180°, 得x＝20°,因此可得三个内角度数分别为40°，60°，80°.
3.如图，D,E分别是AB,AC上的点，若∠A=70°，∠B=60°，DE∥BC，则∠AED的度数是____.【解析】因为∠A=70°，∠B=60°，所以∠C=50°，又因为DE//BC，所以∠AED=∠C=50°.答案：50°
4. 如图，在△ABC中，∠A=60°，∠B=70°，∠ACB的平分线交AB于D，DE∥BC交AC于E，求∠EDC和∠BDC的度数.【解析】∵∠A=60°，∠B=70°，∴∠ACB=180°-60°-70°=50°，∵CD是∠ACB的平分线，∴∠ACD=∠BCD=25°，∵DE∥BC，∴∠EDC=∠BCD=25°.在△BCD中，∠B=70°，∠BCD=25°，∴∠BDC=180°-70°-25°=85°.
通过本课时的学习，需要我们掌握：1.三角形的内角和是180°.2.证明三角形内角和是180°，不仅可以通过实验操作验证，还可以通过严密的推理得到证明.通过平行线将三个内角拼在一起，得到一个平角或构造同旁内角是常用方法.3.△ABC中,∠A+∠B+∠C=180°.推论1: 三角形的一个外角等于和它不相邻的两个内角的和.推论2: 三角形的一个外角大于任何一个和它不相邻的内角.