

贵州省贵阳市清镇市2022-2023学年九年级上学期第一次质检数学试卷(解析版)
展开2022-2023学年贵州省贵阳市清镇市九年级(上)第一次质检数学试卷
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
1.方程x﹣4=0的解是( )
A.4 B.0 C.﹣4 D.无解
2.墨迹覆盖了等式“a2■a2=a4(a≠0)”中的运算符号,则覆盖的运算符号是( )
A.+ B.﹣ C.× D.÷
3.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A.x>﹣1 B.x≥1 C.﹣1<x≤1 D.x≤1
4.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.1 cm B.4 cm C.2 cm D.9 cm
5.下列各组图形中,一定相似的是( )
A.两个平行四边形 B.两个正方形
C.两个矩形 D.两个菱形
6.小星用配方法对一元二次方程x2+2x=3进行求解时,将其化为(x+a)2=b的形式,则a,b的值分别是( )
A.a=1,b=2 B.a=1,b=3 C.a=1,b=4 D.a=﹣1,b=3
7.小明将自己的核酸检测二维码打印在面积为25dm2的正方形纸上,如图所示,为了估计图中黑色部分的面积,他在纸内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的面积约为( )
A.7.5dm2 B.5dm2 C.10dm2 D.15dm2
8.一元二次方程x2+x﹣2=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
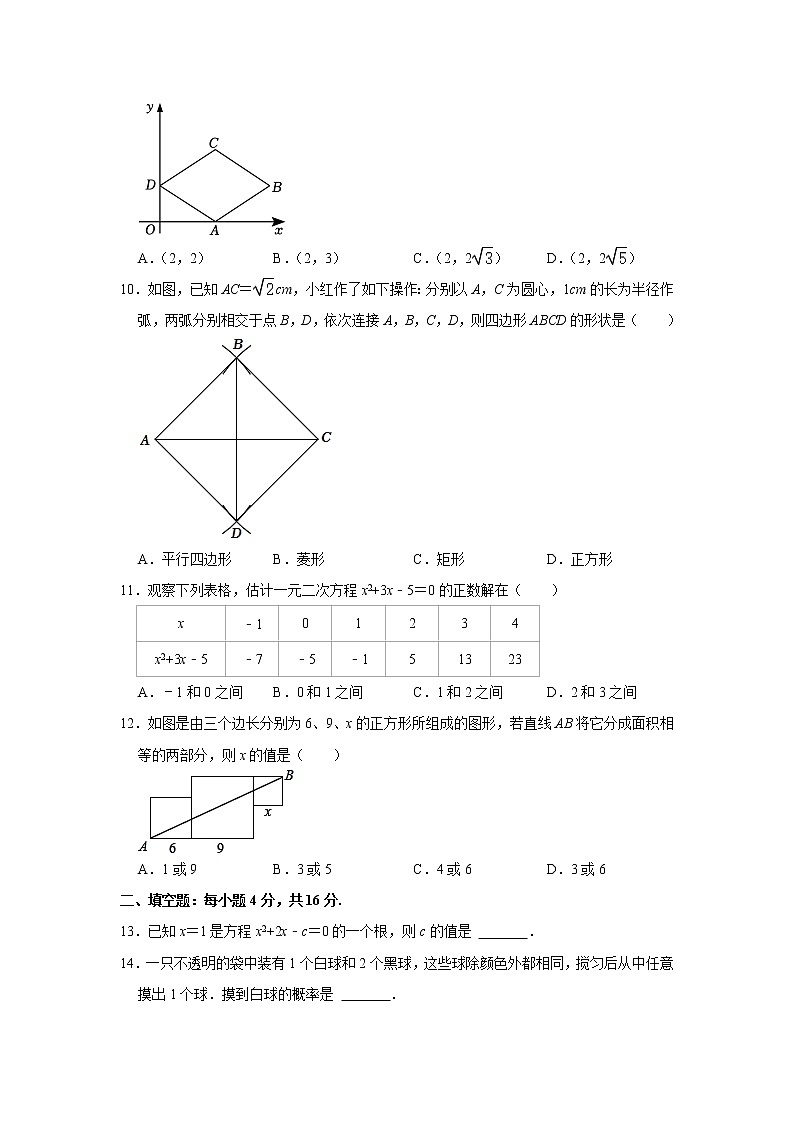
9.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(4,1),点D的坐标是(0,1),点A在x轴上,则点C的坐标是( )
A.(2,2) B.(2,3) C.(2,2) D.(2,2)
10.如图,已知AC=cm,小红作了如下操作:分别以A,C为圆心,1cm的长为半径作弧,两弧分别相交于点B,D,依次连接A,B,C,D,则四边形ABCD的形状是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
11.观察下列表格,估计一元二次方程x2+3x﹣5=0的正数解在( )
x
﹣1
0
1
2
3
4
x2+3x﹣5
﹣7
﹣5
﹣1
5
13
23
A.﹣1和0之间 B.0和1之间 C.1和2之间 D.2和3之间
12.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或9 B.3或5 C.4或6 D.3或6
二、填空题:每小题4分,共16分.
13.已知x=1是方程x2+2x﹣c=0的一个根,则c的值是 .
14.一只不透明的袋中装有1个白球和2个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球.摸到白球的概率是 .
15.如图,在边长为1的3×3网格中,A,B,C,D四点均在格点上,且AB与CD相交于点E,则线段AE的长是 .
16.矩形ABCD中,AB=8,AD=4,点A是y轴正半轴上任意一点,点B在x轴正半轴上.连接OD.则OD的最大值是 .
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(12分)用适当的方法解方程:
(1)x2+4x=12;
(2)x(5x+4)=5x+4.
18.(10分)如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)如果AD=7,DB=3,EC=2,那么AE的长是多少?
(2)如果AB=10,AD=6,EC=3,那么AE的长是多少?
19.(10分)防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A,B,C三个测温通道,某天早晨,该校小红和小星两位同学将随机通过测温通道进入校园.
(1)小红从A测温通道通过的概率是 ;
(2)利用画树状图或列表的方法,求小红和小星从不同的测温通道通过的概率.
20.(10分)数学课上,老师提出一个问题:已知:Rt△ABC,∠ABC=90°.求作:矩形ABCD.小红的作法如下:
作线段AC的垂直平分线交AC于点O,过O点作射线BM,在射线OM上截取OD=OB,连接DA,DC.则四边形ABCD即为所求.
(1)请根据小红的作法,利用尺规作图完成作图(保留作图痕迹);
(2)求证:四边形ABCD是矩形.
21.(10分)随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
22.(10分)如图,在正方形ABCD中,P,H分别为AD和AB上的点,BP与CH交于点E,BP=CH.
(1)求证:BP⊥CH;
(2)若正方形ABCD的边长为4,AP=3,求线段BE的长.
23.(12分)某商场销售某种服装,平均每天可销售20件,每件赢利40元.在每件赢利不少于25元的前提下,若每件降价1元,则每天可多售2件.
(1)若降价x元,则每天销售数量是 件(用含x的代数式表示);
(2)如果每天要赢利1200元,每件应降价多少元?
24.(12分)用充电器给某手机充电时,其屏幕的起始画面如图①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量y(单位:%)与充电时间x(单位:h)的函数图象分别为图②中的线段AB、AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用 小时.
(2)求线段AB、AC对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电﹣耗电﹣充电”的时间恰好是6h,求a的值.
25.(12分)如图1,矩形ABCD与矩形CEFG全等,点B,C,E和点C,D,G分别在同一直线上,且AB=CE=2,BC=EF=4,连接AC,CF.
(1)在图1中,连接AF,则AF= ;
(2)如图2,将图1中的矩形CEFG绕点C逆时针旋转,当CG平分∠ACF时,求点G到AC的距离;
(3)如图3,将图1中的矩形CEFG绕点C顺时针方向旋转,连接AF,DE,两线相交于点M,求证:点M是AF的中点.
2022-2023学年贵州省贵阳市清镇市九年级(上)第一次质检数学试卷(参考答案与详解)
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
1.方程x﹣4=0的解是( )
A.4 B.0 C.﹣4 D.无解
【分析】直接移项即可得出结论.
【解答】解:移项得,x=4.
故选A.
2.墨迹覆盖了等式“a2■a2=a4(a≠0)”中的运算符号,则覆盖的运算符号是( )
A.+ B.﹣ C.× D.÷
【分析】分析所给的式子,结合同底数幂的乘法的法则即可求解.
【解答】解:∵a2×a2=a4,
∴■里的运算符号是:×.
故选:C.
3.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A.x>﹣1 B.x≥1 C.﹣1<x≤1 D.x≤1
【分析】根据数轴上表示的解集得出选项即可.
【解答】解:根据数轴可知:不等式组的解集是x≥1,
故选:B.
4.已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.1 cm B.4 cm C.2 cm D.9 cm
【分析】利用比例线段的定理得到3:2=6:d,然后利用比例的性质求d即可.
【解答】解:根据题意得a:b=c:d,即3:2=6:d,
所以d==4(cm).
故选:B.
5.下列各组图形中,一定相似的是( )
A.两个平行四边形 B.两个正方形
C.两个矩形 D.两个菱形
【分析】根据相似图形的定义,四条边对应成比例,四个角对应相等,对各选项分析判断后利用排除法解答.
【解答】解:A、两个平行四边形不一定相似,故本选项错误;
B、两个正方形,形状相同,大小不一定相同,符合相似性定义,故本选项正确;
C、两个矩形四个角相等,但是各边不一定对应成比例,所以不一定相似,故本选项错误;
D、两个菱形,形状不一定相同,故本选项错误.
故选:B.
6.小星用配方法对一元二次方程x2+2x=3进行求解时,将其化为(x+a)2=b的形式,则a,b的值分别是( )
A.a=1,b=2 B.a=1,b=3 C.a=1,b=4 D.a=﹣1,b=3
【分析】利用解一元二次方程﹣配方法,进行计算即可解答.
【解答】解:x2+2x=3,
x2+2x+1=3+1,
(x+1)2=4,
∴a=1,b=4,
故选:C.
7.小明将自己的核酸检测二维码打印在面积为25dm2的正方形纸上,如图所示,为了估计图中黑色部分的面积,他在纸内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的面积约为( )
A.7.5dm2 B.5dm2 C.10dm2 D.15dm2
【分析】用总面积乘以落入黑色部分的频率稳定值即可.
【解答】解:经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的面积为25×0.6=15(dm2),
故选:D.
8.一元二次方程x2+x﹣2=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
【分析】判断上述方程的根的情况,只要看根的判别式Δ=b2﹣4ac的值的符号就可以了.
【解答】解:∵a=1,b=1,c=﹣2,
∴Δ=b2﹣4ac=1+8=9>0
∴方程有两个不相等的实数根.
故选:A.
9.如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(4,1),点D的坐标是(0,1),点A在x轴上,则点C的坐标是( )
A.(2,2) B.(2,3) C.(2,2) D.(2,2)
【分析】首先连接AC,BD相交于点E,由在菱形ABCD中,点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),可求得点E的坐标,继而求得答案.
【解答】解:连接AC,BD相交于点E,
∵四边形ABCD是菱形,
∴AE=CE,BE=DE,AC⊥BD,
∵点A在x轴上,点B的坐标为(4,1),点D的坐标为(0,1),
∴BD=4,AE=1,
∴DE=BD=2,AC=2AE=2,
∴点C的坐标为:(2,2).
故选:A.
10.如图,已知AC=cm,小红作了如下操作:分别以A,C为圆心,1cm的长为半径作弧,两弧分别相交于点B,D,依次连接A,B,C,D,则四边形ABCD的形状是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
【分析】根据菱形的判定定理解答.
【解答】解:四边形ABCD是菱形,
理由如下:由题意得,AB=AD=CB=CD=1cm,
∴四边形ABCD是菱形,
故选:B.
11.观察下列表格,估计一元二次方程x2+3x﹣5=0的正数解在( )
x
﹣1
0
1
2
3
4
x2+3x﹣5
﹣7
﹣5
﹣1
5
13
23
A.﹣1和0之间 B.0和1之间 C.1和2之间 D.2和3之间
【分析】由表格可发现x2+3x﹣5的值﹣1和5最接近0,再看对应的x的值即可得到答案.
【解答】解:由表可以看出,当x取1与2之间的某个数时,x2+3x﹣5=0,即这个数是x2+3x﹣5=0的一个根.
x2+3x﹣5=0的一个解x的取值范围为1和2之间.
故选:C.
12.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A.1或9 B.3或5 C.4或6 D.3或6
【分析】根据题意列方程,即可得到结论.
【解答】解:如图,
∵若直线AB将它分成面积相等的两部分,
∴(6+9+x)×9﹣x•(9﹣x)=×(6+9+x)×9﹣6×3,
解得x=3,或x=6,
故选:D.
二、填空题:每小题4分,共16分.
13.已知x=1是方程x2+2x﹣c=0的一个根,则c的值是 3 .
【分析】将x=1代入原方程即可求出答案.
【解答】解:将x=1代入原方程可得:1+2﹣c=0,
∴c=3,
故答案为:3.
14.一只不透明的袋中装有1个白球和2个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球.摸到白球的概率是 .
【分析】直接利用概率公式进而计算得出答案.
【解答】解:∵一只不透明的袋中装有1个白球和2个黑球,
∴搅匀后从中任意摸出1个球摸到白球的概率为:.
故答案为:.
15.如图,在边长为1的3×3网格中,A,B,C,D四点均在格点上,且AB与CD相交于点E,则线段AE的长是 .
【分析】取格点F,连接AF、BC,先由勾股定理求得AB=,再证明△AEF∽△BEC,得==,则AE=AB=.
【解答】解:如图,取格点F,连接AF、BC,
由勾股定理得AB==,
∵AF∥BC,
∴△AEF∽△BEC,
∴==,
∴AE=AB=,
∴线段AE的长是,
故答案为:.
16.矩形ABCD中,AB=8,AD=4,点A是y轴正半轴上任意一点,点B在x轴正半轴上.连接OD.则OD的最大值是 4+4 .
【分析】取AB的中点M,连接OM、MD,当OM、MD成一条直线时,OD有最大值,利用勾股定理及直角三角形斜边中线的性质可得答案.
【解答】解:取AB的中点M,连接OM、MD,当OM、MD成一条直线时,OD有最大值,
在Rt△ADM中,DM==4,
在Rt△AOB中,OM=AB=4,
∴OD的最大值是4+4,
故答案为:4+4.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(12分)用适当的方法解方程:
(1)x2+4x=12;
(2)x(5x+4)=5x+4.
【分析】(1)利用解一元二次方程﹣因式分解法,进行计算即可解答;
(2)利用解一元二次方程﹣因式分解法,进行计算即可解答.
【解答】解:(1)x2+4x=12,
x2+4x﹣12=0,
(x+6)(x﹣2)=0,
x+6=0或x﹣2=0,
x1=﹣6,x2=2;
(2)x(5x+4)=5x+4,
x(5x+4)﹣(5x+4)=0,
(5x+4)(x﹣1)=0,
5x+4=0或x﹣1=0,
x1=﹣,x2=1.
18.(10分)如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)如果AD=7,DB=3,EC=2,那么AE的长是多少?
(2)如果AB=10,AD=6,EC=3,那么AE的长是多少?
【分析】(1)(2)利用平行线分线段成比例定理求解即可.
【解答】解:(1)∵DE∥BC,
∴=,
∴=,
∴AE=.
(2)∵AB=10,AD=6,
∴BD=10﹣6=4,
∵DE∥BC,
∴=,
∴=,
∴AE=.
19.(10分)防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A,B,C三个测温通道,某天早晨,该校小红和小星两位同学将随机通过测温通道进入校园.
(1)小红从A测温通道通过的概率是 ;
(2)利用画树状图或列表的方法,求小红和小星从不同的测温通道通过的概率.
【分析】(1)直接利用概率公式求解可得答案;
(2)先列表得出所有等可能结果,从中找到符合条件的结果数,再利用概率公式计算可得.
【解答】解:(1)∵一共有三个通道,小红一次只能通过一个通道,
∴小红从A测温通道通过的概率是.
(2)列表格如下:
A
B
C
A
A,A
B,A
C,A
B
A,B
B,B
C,B
C
A,C
B,C
C,C
由表可知,共有9种等可能的结果,其中小明和小红从不同的测温通道通过的情况有6种,
所以小明和小红从同一个测温通道通过的概率为P==.
20.(10分)数学课上,老师提出一个问题:已知:Rt△ABC,∠ABC=90°.求作:矩形ABCD.小红的作法如下:
作线段AC的垂直平分线交AC于点O,过O点作射线BM,在射线OM上截取OD=OB,连接DA,DC.则四边形ABCD即为所求.
(1)请根据小红的作法,利用尺规作图完成作图(保留作图痕迹);
(2)求证:四边形ABCD是矩形.
【分析】(1)①以点A为圆心,BC长为半径作弧,以点C为圆心,AB长为半径作弧,两弧相交于点D;②连接DA、DC.四边形ABCD为所求矩形;
(2)根据有一个角是直角的平行四边形是矩形证明即可.
【解答】(1)解:如图,四边形ABCD即为所求.
(2)证明:由作法得AD=BC,CD=AB,
∴四边形ABCD为平行四边形,
∵∠ABC=90°,
∴四边形ABCD为矩形.
21.(10分)随着国内新能源汽车的普及,为了适应社会的需求,全国各地都在加快公共充电桩的建设,某省2018年公共充电桩的数量为2万个,2020年公共充电桩的数量为2.88万个.
(1)求2018年至2020年该省公共充电桩数量的年平均增长率;
(2)按照这样的增长速度,预计2021年该省将新增多少万个公共充电桩?
【分析】(1)设2018年至2020年该省公共充电桩数量的年平均增长率为x,利用该省2020年公共充电桩的数量=该省2018年公共充电桩的数量×(1+年平均增长率)2,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)利用该省2021年新增公共充电桩的数量=该省2020年公共充电桩的数量×年平均增长率,即可求出结论.
【解答】解:(1)设2018年至2020年该省公共充电桩数量的年平均增长率为x,
依题意得:2(1+x)2=2.88,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
答:2018年至2020年该省公共充电桩数量的年平均增长率为20%.
(2)2.88×20%=0.576(万个).
答:预计2021年该省将新增0.576万个公共充电桩.
22.(10分)如图,在正方形ABCD中,P,H分别为AD和AB上的点,BP与CH交于点E,BP=CH.
(1)求证:BP⊥CH;
(2)若正方形ABCD的边长为4,AP=3,求线段BE的长.
【分析】(1)由HL证明Rt△ABP≌Rt△BCH,得∠BHC=∠BPA,即可推出结论;
(2)由勾股定理求出BP的长,再根据Rt△ABP≌Rt△BCH,得出BH的长,最后证明△BEH∽△BAP,得出比例式求解即可.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠A=∠CBH=90°,AB=BC,
在Rt△ABP与Rt△BCH中,
,
∴Rt△ABP≌Rt△BCH(HL),
∴∠BHC=∠BPA,
又∵∠ABP=∠EBH,
∴∠BEH=∠A=90°,
∴BP⊥CH;
(2)解:∵AP=3,AB=4,
∴BP==5,
∵Rt△ABP≌Rt△BCH,
∴BH=AP=3,
∵∠ABP=∠EBH,∠BHC=∠BPA,
∴△BEH∽△BAP,
∴,
∴,
∴BE=.
23.(12分)某商场销售某种服装,平均每天可销售20件,每件赢利40元.在每件赢利不少于25元的前提下,若每件降价1元,则每天可多售2件.
(1)若降价x元,则每天销售数量是 (20+2x) 件(用含x的代数式表示);
(2)如果每天要赢利1200元,每件应降价多少元?
【分析】(1)若降价x元,则每件盈利(40﹣x)元,每天销售数量是(20+2x)件,此问得解;
(2)利用总利润=每件盈利×日销售量,即可得出关于x的一元二次方程,解之即可得出x的值,再结合每件赢利不少于25元,即可得出每件应降价10元.
【解答】解:(1)若降价x元,则每件盈利(40﹣x)元,每天销售数量是(20+2x)件.
故答案为:(20+2x).
(2)依题意得:(40﹣x)(20+2x)=1200,
整理得:x2﹣30x+200=0,
解得:x1=10,x2=20,
当x=10时,40﹣x=40﹣10=30>25,符合题意;
当x=20时,40﹣x=40﹣20=20<25,不符合题意,舍去.
答:每件应降价10元.
24.(12分)用充电器给某手机充电时,其屏幕的起始画面如图①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量y(单位:%)与充电时间x(单位:h)的函数图象分别为图②中的线段AB、AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用 4 小时.
(2)求线段AB、AC对应的函数表达式;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电﹣耗电﹣充电”的时间恰好是6h,求a的值.
【分析】(1)由图象可知快速充电器给该手机充满电需2小时,普通充电器给该手机充满电需6小时,即可求解;
(2)利用待定系数法可求解析式;
(3)由“充电﹣耗电﹣充电”的时间恰好是6h,列出方程可求解.
【解答】解:(1)由图象可知快速充电器给该手机充满电需2小时,普通充电器给该手机充满电需6小时,
∴用充电器给该手机充满电时,快速充电器比普通充电器少用4小时;
故答案为:4;
(2)设线段AB的函数表达式为y1=k1x+b1,将(0,20),(2,100)代入y1=k1x+b1,
,
∴,
∴线段AB的函数表达式为:y1=40x+20;
设线段AC的函数表达式为y2=k2x+b2,将(0,20),(6,100)代入y2=k2x+b2,
∴,
∴,
∴线段AC的函数表达式为:y2=+20;
(3)根据题意,得×(6﹣2﹣a)=10a,
解得a=.
答:a的值为.
25.(12分)如图1,矩形ABCD与矩形CEFG全等,点B,C,E和点C,D,G分别在同一直线上,且AB=CE=2,BC=EF=4,连接AC,CF.
(1)在图1中,连接AF,则AF= 2 ;
(2)如图2,将图1中的矩形CEFG绕点C逆时针旋转,当CG平分∠ACF时,求点G到AC的距离;
(3)如图3,将图1中的矩形CEFG绕点C顺时针方向旋转,连接AF,DE,两线相交于点M,求证:点M是AF的中点.
【分析】(1)根据矩形ABCD与矩形CEFG全等,可得矩形CEFG是由矩形ABCD绕点C逆时针旋转得到的,所以∠ACF=90°.然后根据勾股定理即可解决问题;
(2)过点G作GH⊥CF,GQ⊥AC于点H,Q,根据CG平分∠ACF,可得GH=GQ,然后由S△CGF=S矩形CEFG=4,进而可以解决问题;
(3)延长CM交AD延长线于点H,设DE与CF交于点Q,根据矩形的性质证明AD=FQ,然后证明△ADM≌△FQM(AAS),可得AM=FM.进而可以解决问题.
【解答】解:(1)∵矩形ABCD与矩形CEFG全等,
∴矩形CEFG是由矩形ABCD绕点C逆时针旋转得到的,
∴∠ACF=90°.
∵AB=CE=2,BC=EF=4,
∴AC=CF==2,
∴AF=AC=2;
故答案为:2;
(2)解:如图2,过点G作GH⊥CF,GQ⊥AC于点H,Q,
∵CG平分∠ACF,
∴GH=GQ,
∵S△CGF=S矩形CEFG=2×4=4,
∴CF•GH=4,
∴2×GH=4,
∴GH=,
∴CQ=,
∴点G到AC的距离为;
(3)证明:如图,延长CM交AD延长线于点H,设DE与CF交于点Q,
由旋转可知:CD=CE,
∴∠CDE=∠CED,
∵∠CDH=∠CEF=90°,
∴∠QDH=90°﹣∠CDE,∠FEQ=90°﹣∠CED,
∴∠QDH=∠FEQ,
∵AD∥BC,
∴∠QDH=∠DQC,
∵∠DQC=∠FQE,
∴∠FEQ=∠FQE,
∴FE=FQ,
∵AD=FE,
∴AD=FQ,
∵AD∥BC,
∴∠DAM=∠QFM,
在△ADM和△FQM中,
,
∴△ADM≌△FQM(AAS),
∴AM=FM.
∴点M是AF的中点.
贵州省贵阳市清镇市2022-2023学年七年级上学期期末质量监测数学试卷: 这是一份贵州省贵阳市清镇市2022-2023学年七年级上学期期末质量监测数学试卷,共4页。
贵州省贵阳市清镇市2021-2022学年七年级(上)期中数学试卷(含答案): 这是一份贵州省贵阳市清镇市2021-2022学年七年级(上)期中数学试卷(含答案),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
贵州省贵阳市清镇市2022-2023学年九年级上学期第一次质检数学试卷(解析版): 这是一份贵州省贵阳市清镇市2022-2023学年九年级上学期第一次质检数学试卷(解析版),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












