2022-2023学年上学期八年级数学期末模拟测试卷（04）

这是一份2022-2023学年上学期八年级数学期末模拟测试卷（04），共20页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
2022-2023学年上学期八年级数学期末模拟测试卷（04）
一、选择题（本大题共8小题，每小题3分，共24分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．16的算术平方根是（　　）
A．±4 B．±8 C．4 D．﹣4
2．下列图形中是轴对称图形的是（　　）
A． B． C． D．
3．如图，下列条件中，不能证明△ABC≌△DCB的是（　　）

A．AB＝DC，AC＝DB B．AB＝DC，∠ABC＝∠DCB
C．AC＝BD，∠A＝∠D D．BO＝CO，∠A＝∠D
4．下列四组线段中，不能作为直角三角形三条边的是（　　）
A．2，5，6 B．1，1， C．3，4，5 D．5，12，13
5．估计﹣1的值在（　　）
A．1到2之间 B．2到3之间 C．3到4之间 D．4到5之间
6．点P在第二象限内，点P到x轴的距离是6，到y轴的距离是2，那么点P的坐标为（　　）
A．（﹣6，2） B．（﹣2，﹣6） C．（﹣2，6） D．（2，﹣6）
7．一次函数y＝x+1的图象如图所示，下列说法正确的是（　　）

A．y的值随着x的增大而减小
B．函数图象经过第二、三、四象限
C．函数图象与y轴的交点坐标为（1，0）
D．y＝x+1的图象可由y＝x的图象向上平移1个单位长度得到
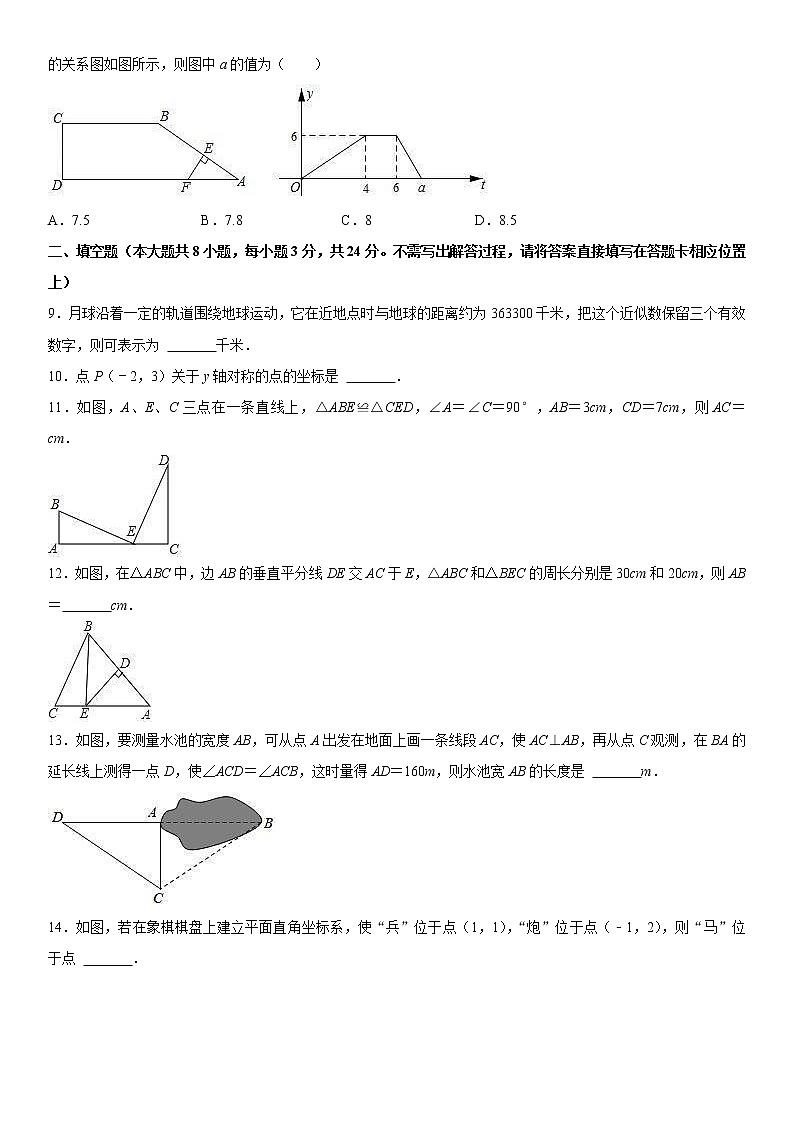
8．如图，在四边形ABCD中，BC∥AD，∠ADC＝90°，点E沿着A→B→C的路径以2cm/s的速度匀速运动，到达点C停止运动，EF始终与直线AB保持垂直，与AD或DC交于点F，记线段EF的长度为ycm，y与时间t（s）的关系图如图所示，则图中a的值为（　　）

A．7.5 B．7.8 C．8 D．8.5
二、填空题（本大题共8小题，每小题3分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
9．月球沿着一定的轨道围绕地球运动，它在近地点时与地球的距离约为363300千米，把这个近似数保留三个有效数字，则可表示为 　 　千米．
10．点P（﹣2，3）关于y轴对称的点的坐标是 　 　．
11．如图，A、E、C三点在一条直线上，△ABE≌△CED，∠A＝∠C＝90°，AB＝3cm，CD＝7cm，则AC＝　 　cm．

12．如图，在△ABC中，边AB的垂直平分线DE交AC于E，△ABC和△BEC的周长分别是30cm和20cm，则AB＝　 　cm．

13．如图，要测量水池的宽度AB，可从点A出发在地面上画一条线段AC，使AC⊥AB，再从点C观测，在BA的延长线上测得一点D，使∠ACD＝∠ACB，这时量得AD＝160m，则水池宽AB的长度是 　 　m．

14．如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点（1，1），“炮”位于点（﹣1，2），则“马”位于点 　 　．

15．如图，某自动感应门的正上方A处装着一个感应器，离地面的高度AB为2.5米，一名学生站在C处时，感应门自动打开了，此时这名学生离感应门的距离BC为1.2米，头顶离感应器的距离AD为1.5米，则这名学生身高CD为 　 　米．

16．已知一次函数y＝mx+n，若y与x的部分对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y
…
10
8
6
4
2
…
则关于x的方程mx+n＝0的解是 　 　．
三、解答题（本大题共9小题，共72分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）（1）求x的值：（x+1）2﹣25＝0；
（2）计算：．





18．（6分）如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于E点，E为AC中点．求证：AD＝CF．






19．（6分）如图，已知AB＝AC，AD＝AE，BD和CE相交于点O．
（1）求证：△ABD≌△ACE；
（2）判断△BOC的形状，并说明理由．






20．（6分）如图，每个小正方形的边长都为1．
（1）求四边形ABCD的周长及面积；
（2）连接BD，判断△BCD的形状．





21．（8分）如图，已知一次函数的图象经过点A（﹣2，﹣5）和B（4，4），与x轴交于点C，与y轴交于点D．
（1）求一次函数的表达式；
（2）求C、D点的坐标，并根据函数图象，直接写出当﹣5＜y＜0时，x的取值范围．





22．（8分）如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别是AC，CD的中点，连接BM，MN，BN．
（1）求证：BM＝MN；
（2）若∠BAD＝60°，AC平分∠BAD，AC＝2．
①求∠BMN的度数；
②求BN的长．






23．（10分）如图，将一张长方形纸片ABCD沿EF折叠，使 C、A两点重合，点D落在点G处．已知AB＝4，BC＝8．
（1）求证：△AEF是等腰三角形；
（2）求线段FD的长．






24．（10分）如图，△ABC三个顶点坐标分别是A（﹣1，0），B（2，2），C（2，1）．
（1）求△ABC的面积；
（2）在x轴上是否存在一点P，使△PAB面积等于△ABC的面积．若存在，请求出点P坐标；若不存在，请说明理由．









25．（12分）某风景区内的公路如图1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计）．第一班车上午8点发车，以后每隔10分钟有一班车从入口处发车，小聪周末到该风景区游玩，上午7：40到达入口处，因还没到班车发车时间，于是从景区入口处出发，沿该公路步行25分钟后到达塔林．小聪及第一班车离入口处的路程y（米）与时间x（分）的关系如图2所示．（假设每一班车速度均相同，小聪步行速度不变）
（1）班车的速度是多少？
（2）当第一班车从入口处到达塔林时，小聪已经在塔林留了多久？
（3）小聪在塔林游玩40分钟后，想坐班车到草甸，则小聪最早能够坐上第 　 　班车．


答案与解析
一、选择题（本大题共8小题，每小题3分，共24分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．16的算术平方根是（　　）
A．±4 B．±8 C．4 D．﹣4
解：∵42＝16，
∴16的算术平方根是4．
答案：C．
2．下列图形中是轴对称图形的是（　　）
A． B． C． D．
解：选项A、C、D均不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项B能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
答案：B．
3．如图，下列条件中，不能证明△ABC≌△DCB的是（　　）

A．AB＝DC，AC＝DB B．AB＝DC，∠ABC＝∠DCB
C．AC＝BD，∠A＝∠D D．BO＝CO，∠A＝∠D
解：A、AB＝DC，AC＝DB，BC＝CB，符合全等三角形的判定定理SSS，能推出△ABC≌△DCB，故本选项不符合题意；
B、AB＝DC，∠ABC＝∠DCB，BC＝CB，符合全等三角形的判定定理SAS，能推出△ABC≌△DCB，故本选项不符合题意；
C、AC＝BD，BC＝CB，∠A＝∠D不能推出△ABC≌△DCB，不符合全等三角形的判定定理，故本选项符合题意．反例如下：
如图所示，AC＝BD，∠A＝∠D，但△ABC与△DCB不全等；

D、∵OB＝OC，∴∠DBC＝∠ACB．∵∠A＝∠D，∴根据三角形内角和定理得出∠ABC＝∠DCB．∠A＝∠D，∠ABC＝∠DCB，BC＝BC，符合全等三角形的判定定理AAS，能推出△ABC≌△DCB，故本选项不符合题意．
答案：C．
4．下列四组线段中，不能作为直角三角形三条边的是（　　）
A．2，5，6 B．1，1， C．3，4，5 D．5，12，13
解：A，22+52≠62，不符合勾股定理的逆定理，不是直角三角形；
B，12+12＝2＝（）2，符合勾股定理的逆定理，是直角三角形；
C，32+42＝25＝52，符合勾股定理的逆定理，是直角三角形；
D，52+122＝169＝132，符合勾股定理的逆定理，是直角三角形．
答案：A．
5．估计﹣1的值在（　　）
A．1到2之间 B．2到3之间 C．3到4之间 D．4到5之间
解：∵＜＜，即3＜＜4，
∴3﹣1＜﹣1＜4﹣1，
即2＜﹣1＜3，
答案：B．
6．点P在第二象限内，点P到x轴的距离是6，到y轴的距离是2，那么点P的坐标为（　　）
A．（﹣6，2） B．（﹣2，﹣6） C．（﹣2，6） D．（2，﹣6）
解：∵点P在第二象限内，点P到x轴的距离是6，到y轴的距离是2，
∴点P的横坐标为﹣2，纵坐标为6，
∴点P的坐标为（﹣2，6）．
答案：C．
7．一次函数y＝x+1的图象如图所示，下列说法正确的是（　　）

A．y的值随着x的增大而减小
B．函数图象经过第二、三、四象限
C．函数图象与y轴的交点坐标为（1，0）
D．y＝x+1的图象可由y＝x的图象向上平移1个单位长度得到
解：A、一次函数y＝x+1中，k＝1＞0，所以y随x的增大而增大，故错误；
B、由图象可知，函数图象经过一、二、三象限，故错误；
C、令x＝0，则y＝1，所以直线与y轴的交点为（0，1），故错误；
D、根据平移的规律，把直线y＝x向上平移1个单位得到直线y＝x+1，故正确．
答案：D．
8．如图，在四边形ABCD中，BC∥AD，∠ADC＝90°，点E沿着A→B→C的路径以2cm/s的速度匀速运动，到达点C停止运动，EF始终与直线AB保持垂直，与AD或DC交于点F，记线段EF的长度为ycm，y与时间t（s）的关系图如图所示，则图中a的值为（　　）

A．7.5 B．7.8 C．8 D．8.5
解：如图所示，作BM⊥AB，交AD于点M，作DN∥BM，交BC于点N，

由题意可知，AB＝4×2＝8（cm），BM＝6cm，DN＝6cm，
∴AM＝，
∴CD＝＝4.8（cm），
∴CN＝＝3.6（cm），
∴a＝6+3.6÷2＝7.8．
答案：B．
二、填空题（本大题共8小题，每小题3分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
9．月球沿着一定的轨道围绕地球运动，它在近地点时与地球的距离约为363300千米，把这个近似数保留三个有效数字，则可表示为 　3.63×105　千米．
解：363300＝3.633×105≈3.63×105．
答案：3.63×105．
10．点P（﹣2，3）关于y轴对称的点的坐标是 　（2，3）　．
解：∵关于x轴对称的点，横坐标相同，纵坐标互为相反数，
∴点P（﹣2，3）关于y轴对称的点的坐标是（2，3）．
答案：（2，3）
11．如图，A、E、C三点在一条直线上，△ABE≌△CED，∠A＝∠C＝90°，AB＝3cm，CD＝7cm，则AC＝　10　cm．

解：∵△ABE≌△CED，AB＝3cm，CD＝7cm，
∴EC＝AB＝3cm，AE＝CD＝7cm，
∴AC＝AE+CE＝7cm+3cm＝10cm，
答案：10．
12．如图，在△ABC中，边AB的垂直平分线DE交AC于E，△ABC和△BEC的周长分别是30cm和20cm，则AB＝　10　cm．

解：∵DE是AB的垂直平分线，
∴EB＝EA，
∵△ABC和△BEC的周长分别是30cm和20cm，
∴AB+AC+BC＝30，CE+BE+BC＝AC+BC＝20，
∴AB＝10（cm），
答案：10．
13．如图，要测量水池的宽度AB，可从点A出发在地面上画一条线段AC，使AC⊥AB，再从点C观测，在BA的延长线上测得一点D，使∠ACD＝∠ACB，这时量得AD＝160m，则水池宽AB的长度是 　160　m．

解：∵AC⊥BD，
∴∠CAD＝∠CAB＝90°，
在△ACD与△ACB中，
，
∴△ACD≌△ACB（ASA），
∴AB＝AD＝160m，
答案：160．
14．如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点（1，1），“炮”位于点（﹣1，2），则“马”位于点 　（4，﹣1）　．

解：如图所示：“马”位于点（4，﹣1）．
答案：（4，﹣1）．

15．如图，某自动感应门的正上方A处装着一个感应器，离地面的高度AB为2.5米，一名学生站在C处时，感应门自动打开了，此时这名学生离感应门的距离BC为1.2米，头顶离感应器的距离AD为1.5米，则这名学生身高CD为 　1.6　米．

解：过点D作DE⊥AB于E，如图所示：
则CD＝BE，DE＝BC＝1.2米＝米，
在Rt△ADE中，AD＝1.5米＝米，
由勾股定理得：AE＝＝＝0.9（米），
∴BE＝AB﹣AE＝2.5﹣0.9＝1.6（米），
∴CD＝BE＝1.6米，
答案：1.6．

16．已知一次函数y＝mx+n，若y与x的部分对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y
…
10
8
6
4
2
…
则关于x的方程mx+n＝0的解是 　x＝3　．
解：把x＝0，y＝6和x＝1，y＝4代入y＝mx+n得，解得，
所以一次函数解析式为y＝﹣2x+6，
当y＝0时，﹣2x+6＝0，解得x＝3，
所以关于x的方程mx+n＝0的解是x＝3．
答案：x＝3．
三、解答题（本大题共9小题，共72分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）（1）求x的值：（x+1）2﹣25＝0；
（2）计算：．
解：（1）（x+1）2﹣25＝0，
（x+1）2＝25，
x+1＝±5，
x＝±5﹣1
∴x1＝4，x2＝﹣6；
（2）原式＝1﹣2+2
＝1．
18．（6分）如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于E点，E为AC中点．求证：AD＝CF．

证明：∵CF∥AB，
∴∠ADE＝∠F，∠A＝∠ECF，
∵E为AC中点．
∴AE＝CE，
在△ADE和△CFE中，，
∴△ADE≌△CFE（AAS），
∴AD＝CF．
19．（6分）如图，已知AB＝AC，AD＝AE，BD和CE相交于点O．
（1）求证：△ABD≌△ACE；
（2）判断△BOC的形状，并说明理由．

证明：（1）∵AB＝AC，∠BAD＝∠CAE，AD＝AE，
∴△ABD≌△ACE（SAS）；
（2）△BOC是等腰三角形，
理由如下：
∵△ABD≌△ACE，
∴∠ABD＝∠ACE，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠ABC﹣∠ABD＝∠ACB﹣∠ACE，
∴∠OBC＝∠OCB，
∴BO＝CO，
∴△BOC是等腰三角形．
20．（6分）如图，每个小正方形的边长都为1．
（1）求四边形ABCD的周长及面积；
（2）连接BD，判断△BCD的形状．

解：（1）根据勾股定理得AB＝＝，AD＝＝，CD＝＝，BC＝＝2，
故四边形ABCD的周长为+3+；
面积为5×5﹣×1×5﹣×1×4﹣1﹣×1×2﹣×2×4＝14.5；
（2）连接BD，
∵BC＝2，CD＝，BD＝5，
∴BC2+CD2＝BD2，
∴∠BCD＝90°，
∴△BCD是直角三角形．

21．（8分）如图，已知一次函数的图象经过点A（﹣2，﹣5）和B（4，4），与x轴交于点C，与y轴交于点D．
（1）求一次函数的表达式；
（2）求C、D点的坐标，并根据函数图象，直接写出当﹣5＜y＜0时，x的取值范围．

解：（1）设一次函数的解析式为y＝kx+b，
∵经过点A（﹣2，﹣5）和B（4，4），
∴，解得，
∴一次函数的表达式为y＝x﹣2；
（2）令y＝0，则x﹣2＝0，解得x＝，
∴C（，0），
由图象可知，当﹣5＜y＜0时，x的取值范围是﹣2＜x＜．
22．（8分）如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别是AC，CD的中点，连接BM，MN，BN．
（1）求证：BM＝MN；
（2）若∠BAD＝60°，AC平分∠BAD，AC＝2．
①求∠BMN的度数；
②求BN的长．

（1）证明：在△CAD中，M、N分别是AC、CD的中点，
∴MN∥AD，MN＝AD，
在Rt△ABC中，∠ABC＝90°，M是AC中点，
∴BM＝AC，
∵AC＝AD，
∴MN＝BM；
（2）解：①∵∠BAD＝60°，AC平分∠BAD，
∴∠BAC＝∠DAC＝30°，
由（1）可知，BM＝AC＝AM＝MC，
∴∠BMC＝∠BAM+∠ABM＝2∠BAM＝60°，
∵MN∥AD，
∴∠NMC＝∠DAC＝30°，
∴∠BMN＝∠BMC+∠NMC＝90°；
②∵∠BMN＝90°，
∴BN2＝BM2+MN2，
由（1）可知MN＝BM＝AC
∵AC＝2，
∴MN＝BM＝1，
∴BN＝或BN＝﹣（舍去）．
23．（10分）如图，将一张长方形纸片ABCD沿EF折叠，使 C、A两点重合，点D落在点G处．已知AB＝4，BC＝8．
（1）求证：△AEF是等腰三角形；
（2）求线段FD的长．

（1）证明：由折叠性质可知，∠AEF＝∠CEF，
由矩形性质可得AD∥BC，
∴∠AFE＝∠CEF，
∴∠AEF＝∠AFE．
∴AE＝AF，
故△AEF为等腰三角形．
（2）解：由折叠可得AE＝CE，设CE＝x＝AE，
则BE＝BC﹣CE＝8﹣x，
∵∠B＝90°，
在Rt△ABE中，有AB2+BE2＝AE2，
即42+（8﹣x）2＝x2，解得：x＝5．
由（1）结论可得AF＝AE＝5，
故FD＝AD﹣AF＝BC﹣AF＝8﹣5＝3．

24．（10分）如图，△ABC三个顶点坐标分别是A（﹣1，0），B（2，2），C（2，1）．
（1）求△ABC的面积；
（2）在x轴上是否存在一点P，使△PAB面积等于△ABC的面积．若存在，请求出点P坐标；若不存在，请说明理由．

解（1）如图，延长BC交x轴于点D，

∵B（2，2），C（2，1），
∴BD⊥x轴，则D（2，0），
∵A（﹣1，0），
∴AD＝3，
∵B（2，2），C（2，1），
∴BC＝1，
∴S△ABC＝×BC•AD＝；
（2）设P点坐标为（x，0），
∵A（﹣1，0），
∴AP＝|x+1|，
∵S△ABP＝S△ABC＝，
∴×AP×2＝，
∴AP＝，
∴|x+1|＝，即x+1＝或x+1＝﹣，
解得x＝或x＝﹣，则P点坐标为（，0）或（﹣，0）．
25．（12分）某风景区内的公路如图1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计）．第一班车上午8点发车，以后每隔10分钟有一班车从入口处发车，小聪周末到该风景区游玩，上午7：40到达入口处，因还没到班车发车时间，于是从景区入口处出发，沿该公路步行25分钟后到达塔林．小聪及第一班车离入口处的路程y（米）与时间x（分）的关系如图2所示．（假设每一班车速度均相同，小聪步行速度不变）
（1）班车的速度是多少？
（2）当第一班车从入口处到达塔林时，小聪已经在塔林留了多久？
（3）小聪在塔林游玩40分钟后，想坐班车到草甸，则小聪最早能够坐上第 　5　班车．

解：（1）班车的速度＝＝150米/分，
∴班车的速度是150米/分；
（2）由题意可设第一班车离入口处的路程y（米）与时间x的关系表达式为：y＝kx+b，
把（20，0），（38，2700）代入y＝kx+b，
得，
解得，
∴第一班车离入口处的路程y（米）与时间x（分）的关系表达式为：y＝150x﹣3000，
当y＝1500时，150x﹣3000＝1500，
解得x＝30，
∴当第一班车从入口处到达塔林时，小聪已经在塔林留了30﹣25＝5分钟；
（3）设小聪坐上了第n班车，则
30﹣25+10（n﹣1）≥40，
解得n≥4.5，
∴小聪最早能坐上第5班车．
答案：5．