2022-2023学年九年级数学上学期期末专题12 选择压轴题分类练（七大考点）

这是一份2022-2023学年九年级数学上学期期末专题12 选择压轴题分类练（七大考点），共26页。
专题12 选择压轴题分类练（七大考点）



实战训练
一．新定义
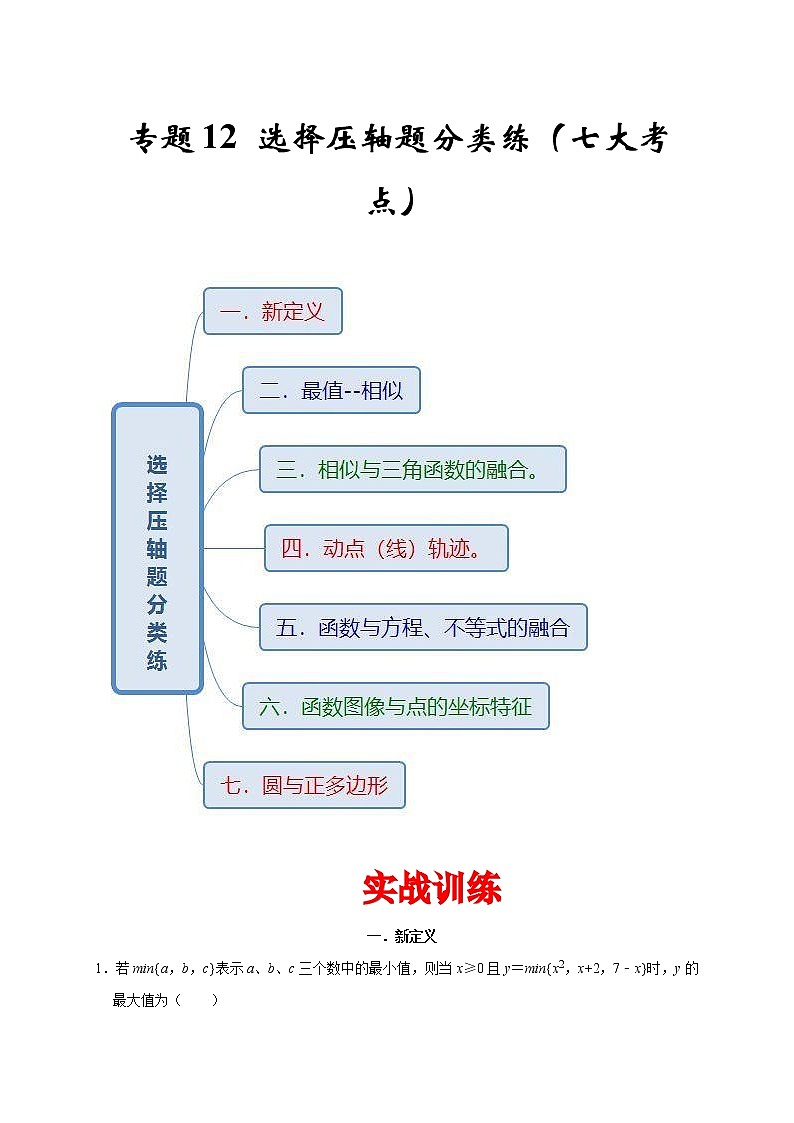
1．若min{a，b，c}表示a、b、c三个数中的最小值，则当x≥0且y＝min{x2，x+2，7﹣x}时，y的最大值为（　　）
A．15−292 B．4 C．112 D．92
2．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形（如图1），它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆形滚木的截面图．

有如下四个结论：
①勒洛三角形是中心对称图形；
②使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动；
③图2中，等边三角形的边长为2，则勒洛三角形的周长为2π；
④图3中，在△ABC中随机取一点，则该点取自勒洛三角形DEF部分的概率为3π−26．
上述结论中，所有正确结论的序号是（　　）
A．①② B．②④ C．②③ D．③④
二．最值--相似
3．如图，在平面直角坐标系中，已知A（﹣2，4）、P（﹣1，0），B为y轴上的动点，以AB为边构造△ABC，使点C在x轴上，∠BAC＝90°，M为BC的中点，则PM的最小值为（　　）

A．172 B．17 C．455 D．5
三．相似与三角函数的融合。
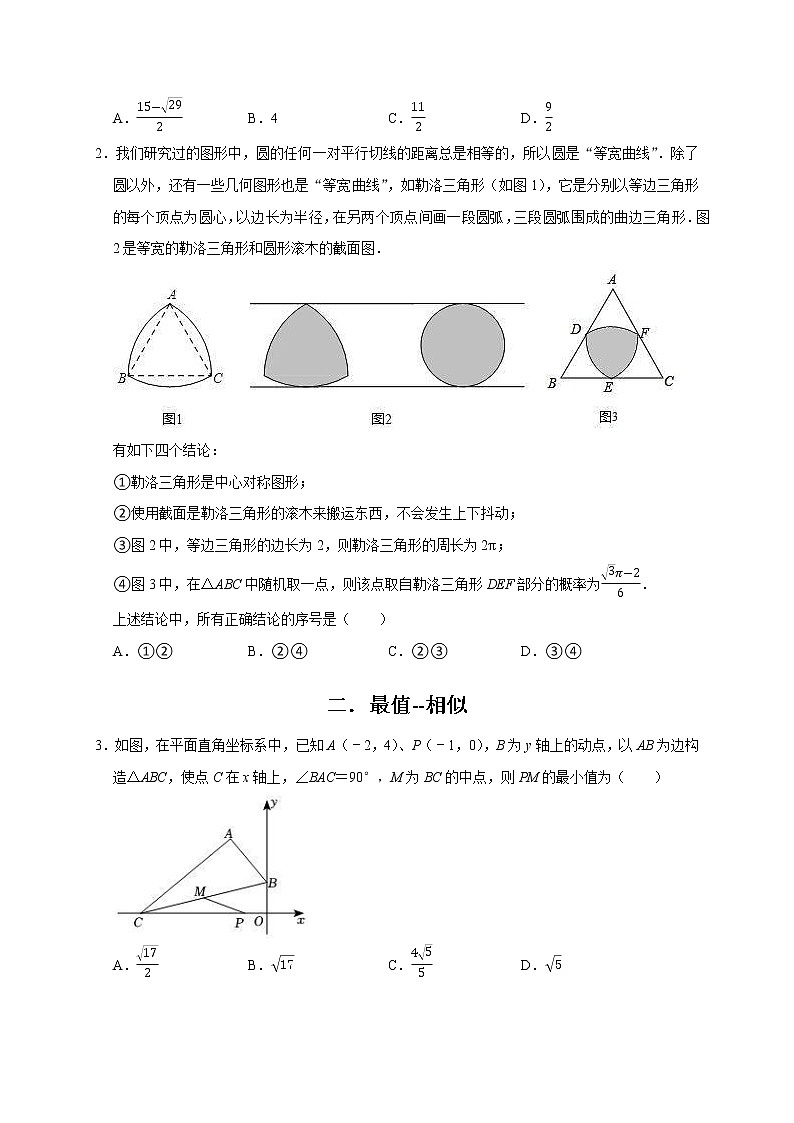
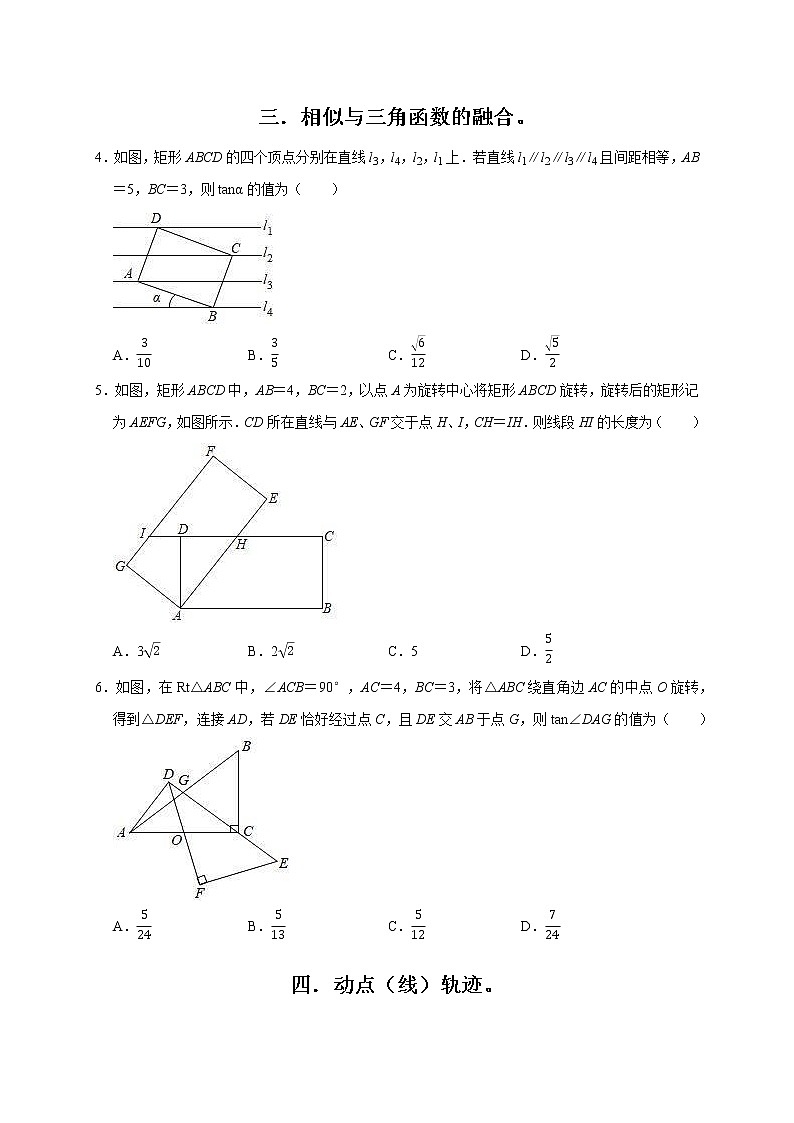
4．如图，矩形ABCD的四个顶点分别在直线l3，l4，l2，l1上．若直线l1∥l2∥l3∥l4且间距相等，AB＝5，BC＝3，则tanα的值为（　　）

A．310 B．35 C．612 D．52
5．如图，矩形ABCD中，AB＝4，BC＝2，以点A为旋转中心将矩形ABCD旋转，旋转后的矩形记为AEFG，如图所示．CD所在直线与AE、GF交于点H、I，CH＝IH．则线段HI的长度为（　　）

A．32 B．22 C．5 D．52
6．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，将△ABC绕直角边AC的中点O旋转，得到△DEF，连接AD，若DE恰好经过点C，且DE交AB于点G，则tan∠DAG的值为（　　）

A．524 B．513 C．512 D．724
四．动点（线）轨迹。
7．如图，在扇形铁皮AOB中，OA＝5，∠AOB＝36°，OB在直线l上．将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA第一次落在l上时，停止旋转，则点O所经过的路线与直线l所围成的面积为（　　）

A．103π B．352π C．6π D．503π
8．如图①，在正方形ABCD中，点P从点D出发，沿着D→A方向匀速运动，到达点A后停止运动．点Q从点D出发，沿着D→C→B→A的方向匀速运动，到达点A后停止运动．已知点P的运动速度为a，图②表示P、Q两点同时出发x秒后，△APQ的面积y与x的函数关系，则点Q的运动速度可能是（　　）

A．13a B．12a C．2a D．3a
9．一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB，BC，CA，OA，OB，OC组成．为记录寻宝者的行进路线，在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（　　）

A．A→O→B B．B→A→C C．B→O→C D．C→B→O
五．函数与方程、不等式的融合
10．欧几里得的《原本》记载，方程x2+ax＝b2的图解法是：画Rt△ABC，使∠ACB＝90°，BC=a2，AC＝b，再在斜边AB上截取BD＝BC．则该方程的一个正根是（　　）

A．AC的长 B．CD的长 C．AD的长 D．BC的长
11．在平面直角坐标系xOy中，点A（a，﹣2a+4）在反比例函数y=kx（k＜0）的图象上，过点A作x轴的垂线，垂足为B．若AB≤4，则k的取值范围是（　　）
A．k≤﹣16 B．k≤﹣2 C．﹣16≤k＜0 D．﹣2≤k＜0
12．若函数y＝x2（x≥0）的图象与直线y＝kx+k+1有公共点，则k的取值范围是（　　）
A．k≤0 B．k≤﹣1
C．k≥﹣1 D．k为任意实数
13．已知关于x的二次函数y＝x2﹣2mx+m2+m+1，其中m为实数，当﹣2≤x≤0时，y的最小值为5，满足条件的m的值为（　　）
A．﹣5或17−12 B．﹣5或−17−12 C．0或17−12 D．0或−17−12
六．函数图像与点的坐标特征
14．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①a＞0；②b＞0； ③方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；④当y＞0时，x的取值范围是﹣1＜x＜3；其中结论正确的个数是（　　）

A．4个 B．3个 C．2个 D．1个
15．如图所示，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于（x1，0），且﹣1＜x1＜0，对称轴x＝1．有下列5个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＞3b；⑤a+b＞m（am+b）（m是不等于1的实数）．其中结论正确个数有（　　）

A．1个 B．2个 C．3个 D．4个
16．如图，现要在抛物线y＝x（4﹣x）上找点P（a，b），针对b的不同取值，所找点P的个数，四人的说法如下，
甲：若b＝﹣1，则点P的个数为3；乙：若b＝0，则点P的个数为1；丙：若b＝4，则点P的个数为1；丁：若b＝5，则点P的个数为0．
其中说法正确的有（　　）

A．0个 B．1个 C．2个 D．3个
17．如图，抛物线y＝ax2+bx﹣8交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C、D两点（点C在点D的左边），对称轴为直线x＝﹣5，连接BD、AD、BC，若点A关于直线BD的对称点恰好落在线段OC上，下列结论中错误的是（　　）

A．B的坐标是（﹣10，﹣8） B．a=112
C．D点坐标为（6，0） D．b=45
七．圆与正多边形
18．如图，正三角形PMN的顶点分别是正六边形ABCDEF三边的中点，则三角形PMN与六边形ABCDEF的面积之比（　　）

A．1：2 B．1：3 C．2：3 D．3：8
19．如图，两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上，点P在ABI上，则tan∠API的值是（　　）

A．23 B．22 C．2 D．1
20．已知四边形ABCD，下列命题：①若∠A+∠C＝180°，则四边形ABCD一定存在外接圆；②若四边形ABCD内存在一点到四个顶点的距离相等，则∠A+∠C＝∠B+∠D；③若四边形ABCD内存在一点到四条边的距离相等，则AB+CD＝BC+AD，其中，真命题的个数为（　　）
A．0 B．1 C．2 D．3

一．新定义
1．若min{a，b，c}表示a、b、c三个数中的最小值，则当x≥0且y＝min{x2，x+2，7﹣x}时，y的最大值为（　　）
A．15−292 B．4 C．112 D．92
试题分析：用特殊值法得出答案．
答案详解：解：方法一、x＝0时，y＝min{0，2，7}＝0．
当x＝1时，y＝min{1，3，6}＝1．
当x＝2时，y＝min{4，6，5}＝4．
当x＝3时，y＝min{9，11，4}＝4．
当x＝4时，y＝min{16，6，3}＝3．
当x＝2.5时，y＝min{6.25，4.5，4.5}＝4.5．
∴y的最大值是92．
方法二、由图象可得当x=52时，y有最大值＝7−52=92．

所以选：D．
2．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”．除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形（如图1），它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形．图2是等宽的勒洛三角形和圆形滚木的截面图．

有如下四个结论：
①勒洛三角形是中心对称图形；
②使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动；
③图2中，等边三角形的边长为2，则勒洛三角形的周长为2π；
④图3中，在△ABC中随机取一点，则该点取自勒洛三角形DEF部分的概率为3π−26．
上述结论中，所有正确结论的序号是（　　）
A．①② B．②④ C．②③ D．③④
试题分析：根据轴对称的性质，等边三角形的性质，求出勒洛三角形的面积，由测度比是面积比逐一判断即可﹒
答案详解：解：①勒洛三角形是轴对称图形，不是中心对称图形，故①错误；
②夹在平行线之间的勒洛三角形无论怎么滚动，平行线间的距离始终不变，使用截面是勒洛三角形的滚木来搬运东西，不会发生上下抖动，故②正确；
③∵等边三角形DEF的边长为2，
∴勒洛三角形的周长＝3×60⋅π⋅2180=2π，故③正确；
④如图，设△ABC的边长为2，则正三角形DEF的边长为1，

以D为圆心的扇形面积是π⋅126=π6，
△DEF的面积是12×1×1×32=34，
∴勒洛三角形的面积为3个扇形面积减去2个正三角形面积，即图中勒洛三角形面积为3×（π6−34）+34=π−32，△ABC的面积为3，
∴所求概率为π−323=3π−36，故④错误；
所以选：C．
二．最值--相似
3．如图，在平面直角坐标系中，已知A（﹣2，4）、P（﹣1，0），B为y轴上的动点，以AB为边构造△ABC，使点C在x轴上，∠BAC＝90°，M为BC的中点，则PM的最小值为（　　）

A．172 B．17 C．455 D．5
试题分析：作AH⊥y轴，CE⊥AH，证明△AHB∽△CEA，根据相似三角形的性质得到AE＝2BH，求出点M的坐标，根据两点间的距离公式用x表示出PM，根据二次函数的性质解答即可．
答案详解：解：如图，过点A作AH⊥y轴于H，过点C作CE⊥AH于E，

则四边形CEHO是矩形，
∴OH＝CE＝4，
∵∠BAC＝∠AHB＝∠AEC＝90°，
∴∠ABH+∠HAB＝90°，∠HAB+∠EAC＝90°，
∴∠ABH＝∠EAC，
∴△AHB∽△CEA，
∴AHEC=BHAE，即24=BHAE，
∴AE＝2BH，
设BH＝x，则AE＝2x，
∴OC＝HE＝2+2x，OB＝4﹣x，
∴B（0，4﹣x），C（﹣2﹣2x，0），
∵BM＝CM，
∴M（﹣1﹣x，4−x2），
∵P（﹣1，0），
∴PM=x2+(4−x2)2=54(x−45)2+165，
∴PM的最小值为165=455；
所以选：C．
三．相似与三角函数的融合。
4．如图，矩形ABCD的四个顶点分别在直线l3，l4，l2，l1上．若直线l1∥l2∥l3∥l4且间距相等，AB＝5，BC＝3，则tanα的值为（　　）

A．310 B．35 C．612 D．52
试题分析：过C作CF⊥l4于点F，交l3于点E，设CB交l3于点G，证△CEG∽△CFB，得CGCB=CECF=12，则GB＝CG=32，再由平行线的性质得∠α＝∠GAB，然后由锐角三角函数定义求出tan∠BAG=310，即可求解．
答案详解：解：过C作CF⊥l4于点F，交l3于点E，设CB交l3于点G，
由题意得：GE∥BF，CE＝EF，
∴△CEG∽△CFB，
∴CGCB=CECF=12，
∵BC＝3，
∴CG=12BC=32，
∴GB＝CG=32，
∵l3∥l4，
∴∠α＝∠GAB，
∵四边形ABCD是矩形，AB＝5，
∴∠ABG＝90°，
∴tan∠BAG=BGAB=325=310，
∴tanα＝tan∠BAG=310，
所以选：A．

5．如图，矩形ABCD中，AB＝4，BC＝2，以点A为旋转中心将矩形ABCD旋转，旋转后的矩形记为AEFG，如图所示．CD所在直线与AE、GF交于点H、I，CH＝IH．则线段HI的长度为（　　）

A．32 B．22 C．5 D．52
试题分析：由“HL”可证Rt△AGI≌Rt△ADI，可得∠GAI＝∠DAI，由余角的性质可得∠IAH＝∠AID，可证IH＝AH，通过证明△ADI∽△CDA，可得ADDC=DIAD，可求DI＝1，即可求解．
答案详解：解：如图，连接AI，AC，

∵以点A为旋转中心将矩形ABCD旋转，旋转后的矩形记为AEFG，
∴AG＝AD，∠GAE＝∠DAB＝90°，
在Rt△AGI和Rt△ADI中，
AG=ADAI=AI，
∴Rt△AGI≌Rt△ADI（HL），
∴∠GAI＝∠DAI，
∴90°﹣∠GAI＝90°﹣∠DAI，
∴∠IAH＝∠AID，
∴IH＝AH，
又∵IH＝HC，
∴IH＝HC＝AH，
∴∠IAC＝90°，
∴∠DAI+∠DAC＝90°，
又∵∠DAC+∠DCA＝90°，
∴∠DAI＝∠DCA，
又∵∠ADI＝∠ADC＝90°，
∴△ADI∽△CDA，
∴ADDC=DIAD，
∴24=DI2，
∴DI＝1，
∴CI＝ID+CD＝5，
∴IH=12IC=52，
所以选：D．
6．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，将△ABC绕直角边AC的中点O旋转，得到△DEF，连接AD，若DE恰好经过点C，且DE交AB于点G，则tan∠DAG的值为（　　）

A．524 B．513 C．512 D．724
试题分析：连接OG，由勾股定理求出AB＝5，由直角三角形的性质求出CG，CD，AD的长，由锐角三角函数的定义可得出答案．
答案详解：解：连接OG，

在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，
∴AB=AC2+BC2=42+32=5，
∵点O是AC边的中点，
∴OC＝OA＝OD=12AC＝2，
∴∠GCO＝∠ODC＝∠BAC，∠ADC＝90°，
∴AG＝CG，
∴OG⊥AC，
在Rt△ABC中，sin∠BAC=BCAB=35，cos∠BAC=ACAB=45，
∴sin∠OCG=35，cos∠OCG=45，
在Rt△OCG中，CG=OCcos∠OCG=52，在Rt△ACD中，CD＝AC•cos∠OCG=165，AD＝AC•sin∠OCG=125，
∴DG＝CD﹣CG=165−52=710，
∴tan∠DAG=DGAD=710125=724．
所以选：D．
四．动点（线）轨迹。
7．如图，在扇形铁皮AOB中，OA＝5，∠AOB＝36°，OB在直线l上．将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA第一次落在l上时，停止旋转，则点O所经过的路线与直线l所围成的面积为（　　）

A．103π B．352π C．6π D．503π
试题分析：点O所经过的路线是2段弧和一条线段，一段是以点B为圆心，5为半径，圆心角为90°的弧，另一段是一条线段，和弧AB一样长的线段，最后一段是以点A为圆心，5为半径，圆心角为90°的弧，从而得出答案．
答案详解：解：如图，当OA第1次落在l上时：点O所经过的路线与直线l所围成的面积为＝2×90π⋅52360+5•36π⋅5180=352π．

所以选：B．
8．如图①，在正方形ABCD中，点P从点D出发，沿着D→A方向匀速运动，到达点A后停止运动．点Q从点D出发，沿着D→C→B→A的方向匀速运动，到达点A后停止运动．已知点P的运动速度为a，图②表示P、Q两点同时出发x秒后，△APQ的面积y与x的函数关系，则点Q的运动速度可能是（　　）

A．13a B．12a C．2a D．3a
试题分析：本题根据动点之间相对位置，讨论形成图形的面积的变化趋势即可，适于采用筛选法．
答案详解：解：本题采用筛选法．首先观察图象，可以发现图象由三个阶段构成，即△APQ的顶点Q所在边应有三种可能．
当Q的速度低于点P时，当点P到达A时，点Q还在DC上运动，之后，因A、P重合，△APQ的面积为零，画出图象只能由一个阶段构成，故A、B错误；
当Q的速度是点P速度的2倍，当点P到点A时，点Q到点B，之后，点A、P重合，△APQ的面积为0．期间△APQ面积的变化可以看成两个阶段，与图象不符，C错误．
所以选：D．
9．一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB，BC，CA，OA，OB，OC组成．为记录寻宝者的行进路线，在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（　　）

A．A→O→B B．B→A→C C．B→O→C D．C→B→O
试题分析：根据函数的增减性：不同的观察点获得的函数图象的增减性不同，可得答案．
答案详解：解：A、从A点到O点y随x增大一直减小，从O到B先减小后增发，故A不符合题意；
B、从B到A点y随x的增大先减小再增大，从A到C点y随x的增大先减小再增大，但在A点距离最大，故B不符合题意；
C、从B到O点y随x的增大先减小再增大，从O到C点y随x的增大先减小再增大，在B、C点距离最大，故C符合题意；
D、从C到M点y随x的增大而减小，一直到y为0，从M点到B点y随x的增大而增大，明显与图象不符，故D不符合题意；
所以选：C．
五．函数与方程、不等式的融合
10．欧几里得的《原本》记载，方程x2+ax＝b2的图解法是：画Rt△ABC，使∠ACB＝90°，BC=a2，AC＝b，再在斜边AB上截取BD＝BC．则该方程的一个正根是（　　）

A．AC的长 B．CD的长 C．AD的长 D．BC的长
试题分析：（方法一）在Rt△ABC中，由勾股定理可得出AC2+BC2＝AB2，结合AB＝AD+BD，AC＝b，BD＝BC=a2，即可得出AD2+aAD＝b2，进而可得出AD的长是方程x2+ax＝b2的一个正根；
（方法二）利用公式法可得出x=−a+a2+4b22是方程x2+ax＝b2的一个正根，由勾股定理可得出a2+4b2＝4AB2，将其代入x=−a+a2+4b22中可得出x=−a+a2+4b22=AB−a2，再结合各边的长度，即可得出AD的长是方程x2+ax＝b2的一个正根．
答案详解：解：（方法一）在Rt△ABC中，由勾股定理可得AC2+BC2＝AB2．
∵AC＝b，BD＝BC=a2，
∴b2+（a2）2＝（AD+a2）2＝AD2+aAD+（a2）2，
∴AD2+aAD＝b2．
∵AD2+aAD＝b2与方程x2+ax＝b2相同，且AD的长度为正数，
∴AD的长是方程x2+ax＝b2的一个正根．
所以选：C．
（方法二）原方程可变形为x2+ax﹣b2＝0，
∴Δ＝a2+4b2，
∴x=−a±a2+4b2a，其中正根为x=−a+a2+4b22．
∵BC2+AC2＝AB2，即a24+b2＝AB2，
∴a2+4b2＝4AB2，
∴x=−a+a2+4b22=−a+2AB2=AB−a2=AB﹣BD＝AD，
∴AD的长是方程x2+ax＝b2的一个正根．
所以选：C．

11．在平面直角坐标系xOy中，点A（a，﹣2a+4）在反比例函数y=kx（k＜0）的图象上，过点A作x轴的垂线，垂足为B．若AB≤4，则k的取值范围是（　　）
A．k≤﹣16 B．k≤﹣2 C．﹣16≤k＜0 D．﹣2≤k＜0
试题分析：根据题意得到AB＝|﹣2a+4|≤4，然后分A在第四象限或第二象限两种情况讨论即可求得a的取值，进而求得k的取值．
答案详解：解：∵点A（a，﹣2a+4）在反比例函数y=kx（k＜0）的图象上，过点A作x轴的垂线，垂足为B．AB≤4，
∴AB＝|﹣2a+4|≤4，
当a＞0时，则2a﹣4≤4，解得0＜a≤4，
∴k＝a（﹣2a+4）＝﹣2a2+4a＝﹣2（a﹣1）2+2≥﹣16，
当a＜0时，则﹣2a+4≤4，解得a≥0，不合题意舍去，
∴k＝a（﹣2a+4）＝﹣2a2+4a＝﹣2（a﹣1）2+2≥﹣16，
故k的取值范围是﹣16≤k＜0，
所以选：C．
12．若函数y＝x2（x≥0）的图象与直线y＝kx+k+1有公共点，则k的取值范围是（　　）
A．k≤0 B．k≤﹣1
C．k≥﹣1 D．k为任意实数
试题分析：根据一次函数和二次函数的性质判断即可．
答案详解：解：函数y＝x2（x≥0）的图象在第一象限，
当k＞0时，k+1＞0时，直线经过一二三象限，与函数y＝x2（x≥0）的图象有公共点；
当k＜0时，k+1≥0时，直线经过一二四象限或二四象限，与函数y＝x2（x≥0）的图象有公共点；
k＜0时，k+1＜0时，直线经过二三四象限，与函数y＝x2（x≥0）的图象无公共点；
故若函数y＝x2（x≥0）的图象与直线y＝kx+k+1有公共点，则k的取值范围是k≥﹣1，
所以选：C．
13．已知关于x的二次函数y＝x2﹣2mx+m2+m+1，其中m为实数，当﹣2≤x≤0时，y的最小值为5，满足条件的m的值为（　　）
A．﹣5或17−12 B．﹣5或−17−12 C．0或17−12 D．0或−17−12
试题分析：根据题意和二次函数的性质，利用分类讨论的方法可以求得m的值，本题得以解决．
答案详解：解：∵二次函数y＝x2﹣2mx+m2+m+1＝（x﹣m）2+m+1，
∴该函数的对称轴为直线x＝m，函数图象开口向上，
∵当﹣2≤x≤0时，y的最小值为5，
∴当m＜﹣2时，5＝（﹣2﹣m）2+m+1，得m1＝﹣5，m2＝0（舍去）；
当﹣2≤m≤0时，m+1＝5，得m＝4（舍去）；
当m＞0时，5＝（0﹣m）2+m+1，得m3=−1+172，m4=−1−172（舍去）；
由上可得，m的值是﹣5或−1+172，
所以选：A．
六．函数图像与点的坐标特征
14．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①a＞0；②b＞0； ③方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；④当y＞0时，x的取值范围是﹣1＜x＜3；其中结论正确的个数是（　　）

A．4个 B．3个 C．2个 D．1个
试题分析：根据二次函数的图象与性质即可求出答案．
答案详解：解：①由图象可知：抛物线开口向下，
∴a＜0，故①错误；
②∵对称轴为x＝1，
∴−b2a=1，
∴b＝﹣2a＞0，故②正确；
③（﹣1，0）关于直线x＝1的对称点为（3，0），
∴ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3，故③正确；
④当y＞0时，由图象可知：﹣1＜x＜3，故④正确；
所以选：B．
15．如图所示，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于（x1，0），且﹣1＜x1＜0，对称轴x＝1．有下列5个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＞3b；⑤a+b＞m（am+b）（m是不等于1的实数）．其中结论正确个数有（　　）

A．1个 B．2个 C．3个 D．4个
试题分析：根据函数图象和二次函数的性质可以判断题目中各个小题的结论是否成立，从而可以解答本题．
答案详解：解：①由图象可知：a＜0，b＞0，c＞0，abc＜0，故此选项错误；
②当x＝﹣1时，y＝a﹣b+c＜0，即b＞a+c，故此选项错误；
③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故此选项正确；
④当x＝3时函数值小于0，y＝9a+3b+c＜0，且x=−b2a=1，
即a=−b2，代入得9×（−b2）+3b+c＜0，得2c＜3b，故此选项错误；
⑤当x＝1时，y的值最大．
所以a+b+c＞am2+bm+c（m是不等于1的实数），
故a+b＞am2+bm，即a+b＞m（am+b），故此选项正确．
故③⑤正确．
所以选：B．
16．如图，现要在抛物线y＝x（4﹣x）上找点P（a，b），针对b的不同取值，所找点P的个数，四人的说法如下，
甲：若b＝﹣1，则点P的个数为3；乙：若b＝0，则点P的个数为1；丙：若b＝4，则点P的个数为1；丁：若b＝5，则点P的个数为0．
其中说法正确的有（　　）

A．0个 B．1个 C．2个 D．3个
试题分析：把P点的坐标代入函数的解析式，再根据根的判别式逐个判断即可．
答案详解：解：甲：当b＝﹣1时，（4﹣a）＝﹣1，
整理得：a2﹣4a﹣1＝0，
△＝（﹣4）2﹣4×1×（﹣1）＝20＞0，
方程有两个不相等的实数根，
即此时点P的个数为2，故甲的说法错误；
乙：当b＝0时，a（4﹣a）＝0，
解得：a＝0或4，
即此时点P的个数为2，故乙的说法错误；
丙：当b＝4时，a（4﹣a）＝4，
整理得：a2﹣4a+4＝0，
△＝（﹣4）2﹣4×1×4＝0，
方程有两个相等的实数根，
即此时点P的个数为1，故丙的说法正确；
丁：当b＝5时，a（4﹣a）＝5，
整理得：a2﹣4a+5＝0，
△＝（﹣4）2﹣4×1×5＝﹣4＜0，
方程没有实数根，
即此时点P的个数为0，故丁的说法正确；
所以正确的个数是2个，
所以选：C．
17．如图，抛物线y＝ax2+bx﹣8交y轴于点A，交过点A且平行于x轴的直线于另一点B，交x轴于C、D两点（点C在点D的左边），对称轴为直线x＝﹣5，连接BD、AD、BC，若点A关于直线BD的对称点恰好落在线段OC上，下列结论中错误的是（　　）

A．B的坐标是（﹣10，﹣8） B．a=112
C．D点坐标为（6，0） D．b=45
试题分析：先确定A（0，﹣8），利用对称性得到B（﹣10，﹣8），则可对A选项进行判断；设点A关于直线BD的对称点A′恰好落在线段OC上，如图，利用折叠的性质得到DA＝DA′，∠ADB＝∠A′DB，则可证明∠ABD＝∠ADB，所以AD＝AB＝10，利用勾股定理计算出OD得到D（6，0），则可对C选项进行判断；利用对称性确定C（﹣16，0），利用交点式求出抛物线解析式，从而可对B、D选项进行判断．
答案详解：解：当x＝0时，y＝ax2+bx﹣8＝﹣8，则A（0，﹣8），
∵抛物线的对称轴为直线x＝﹣5，AB∥x轴，
∴点A与点B关于直线x＝﹣5对称，
∴B（﹣10，﹣8），所以A选项的结论正确；
设点A关于直线BD的对称点A′恰好落在线段OC上，如图，
∴DA＝DA′，∠ADB＝∠A′DB，
∵AB∥DA′，
∴∠ABD＝∠A′DB，
∴∠ABD＝∠ADB，
∴AD＝AB＝10，
在Rt△OAD中，OD=102−82=6，
∴D（6，0），所以C选项的结论正确；
∴C（﹣16，0），
设抛物线解析式为y＝a（x+16）（x﹣6），
即y＝ax2+10x﹣96a，
∴﹣96a＝﹣8，
∴a=112，所以B选项的结论正确，D选项的结论错误．
所以选：D．

七．圆与正多边形
18．如图，正三角形PMN的顶点分别是正六边形ABCDEF三边的中点，则三角形PMN与六边形ABCDEF的面积之比（　　）

A．1：2 B．1：3 C．2：3 D．3：8
试题分析：连接BE，设正六边形的边长为a，首先证明△PMN是等边三角形，分别求出△PMN，正六边形ABCDEF的面积即可．
答案详解：解：连接BE，设正六边形的边长为a．则AF＝a，BE＝2a，AF∥BE，
∵AP＝PB，FN＝NE，
∴PN=12（AF+BE）＝1.5a，
同法可得PM＝MN＝1.5a，
∵△PMN是等边三角形，
∴S△PMNS正六边形ABCDEF=34×(1.5a)26×34×a2=38，
所以选：D．

19．如图，两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上，点P在ABI上，则tan∠API的值是（　　）

A．23 B．22 C．2 D．1
试题分析：如图，连接AE，EI，AH，过点J作JM⊥EI于M．证明∠AIH＝90°，设HI＝a，求出AI即可解决问题．
答案详解：解：如图，连接AE，EI，AH，过点J作JM⊥EI于M．

∵ABCDEF是正六边形，
∴∠DEF＝∠F＝120°，
∵FA＝FE，
∴∠FEA＝∠FAE＝30°，
∴∠AED＝90°，
同法可证，∠DEI＝∠EIH＝90°，
∴∠AED+∠DEI＝180°，
∴A，E，I共线，
设IH＝IJ＝JE＝a，
∵JM⊥EI，
∴EM＝MI=32a，
∴AI＝2EI＝23a，
∵∠API＝∠AHI，
∴tan∠API＝tan∠AHI=AIHI=23aa=23，
所以选：A．
20．已知四边形ABCD，下列命题：①若∠A+∠C＝180°，则四边形ABCD一定存在外接圆；②若四边形ABCD内存在一点到四个顶点的距离相等，则∠A+∠C＝∠B+∠D；③若四边形ABCD内存在一点到四条边的距离相等，则AB+CD＝BC+AD，其中，真命题的个数为（　　）
A．0 B．1 C．2 D．3
试题分析：根据四边形的有关知识进行判断即可．
答案详解：解：①若∠A+∠C＝180°，所以∠B+∠D＝180°，
则四边形ABCD一定存在外接圆，是真命题；
②若四边形ABCD内存在一点到四个顶点的距离相等，所以OA＝OB＝OC＝OD，
所以A，B，C，D四点共圆，
则四边形是圆内接四边形，
则∠A+∠C＝∠B+∠D，是真命题；
③依照题意，画出图形，如图所示．

∵如果四边形内的一个点到四条边的距离相等，
∴四边形ABCD为⊙O的外切四边形，
∴AE＝AN，DN＝DM，CM＝CF，BF＝BE，
∵AD＝AN+DN，BC＝BF+CF，AB＝AE+BE，CD＝CM+DM，
∴AD+BC＝AB+CD，是真命题；
所以选：D．