2022-2023学年七年级数学上学期期末【压轴60题考点专练】

这是一份2022-2023学年七年级数学上学期期末【压轴60题考点专练】，共135页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
七年级上学期期末【压轴60题考点专练】
一、单选题
1．（2020·江苏南京·七年级期末）如图是一个切去了一个角的正方体纸盒，切面与棱的交点A，B，C均是棱的中点，现将纸盒剪开展成平面，则展开图不可能是（　　）
​
A．​ B．
C．​ D．​
2．（2022·江苏无锡·七年级期末）如图，长方形ABCD中，AB＝8cm，AD＝6cm，P，Q两动点同时出发，分别沿着长方形的边长运动，P点从B点出发，顺时针旋转一圈，到达B点后停止运动，Q点的运动路线为B→C→D，P，Q点的运动速度分别为2cm/秒，1cm/秒，当一个动点到达终点时，另一个动点也同时停止运动．设两动点运动的时间为t秒，要使△BDP和△ACQ的面积相等，满足条件的t值的个数为（　　）

A．2 B．3 C．4 D．5
3．（2020·江苏苏州·七年级期末）满足的整数对共有（    ）
A．个 B．个 C．个 D．个
4．（2021·江苏南京·七年级期末）有理数a、b、c在数轴上对应点的位置如图所示，若|b|＞|c|，则下列结论中正确的是（    ）

A．abc＜0 B．b＋c＜0 C．a＋c＞0 D．ac＞ab
二、填空题
5．（2022·江苏扬州·七年级期末）如图，在三角形中，，点为边上一个动点，连接，把三角形沿着折叠，当时，则______．

6．（2022·江苏·射阳县第六中学七年级期末）如图，在长方形ABCD中，AB＝6cm，BC＝8cm，点E是AB上的一点，且AE＝2BE．点P从点C出发，以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动，最终到达点E．设点P运动时间为ts，若三角形PCE的面积为18cm2，则t的值为 _____．

7．（2020·江苏苏州·七年级期末）本学期，我们做过“抢30”的游戏，如果将游戏规则中“不可以连说三个数，谁先抢到30谁就获胜”，改为“每次可以连说三个数，谁先抢到33谁就获胜”，那么采取适当策略，其结果_____者胜
8．（2020·江苏·射阳县实验初级中学七年级期末）古希腊 Pythagoras学派把自然数与小石子堆放的形状比拟，借此把自然数分类，图中的五角形数别表示分别表示数1、5、12、22、…，那么第n个五角形数是_______ (n为正整数)

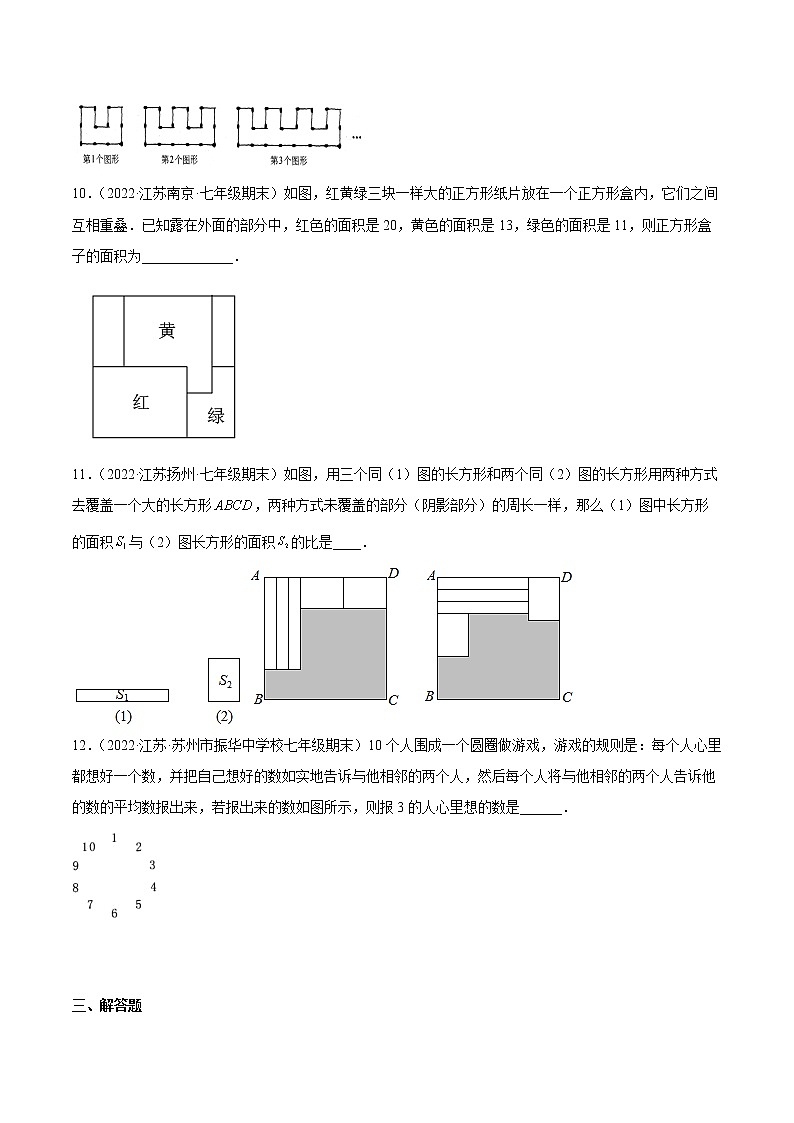
9．（2020·江苏扬州·七年级期末）用火柴棒按如图所示方式搭图形，按照这种方式搭下去，搭第2020个图形需火柴棒的根数是________．    

10．（2022·江苏南京·七年级期末）如图，红黄绿三块一样大的正方形纸片放在一个正方形盒内，它们之间互相重叠．已知露在外面的部分中，红色的面积是20，黄色的面积是13，绿色的面积是11，则正方形盒子的面积为_____________．

11．（2022·江苏扬州·七年级期末）如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积与（2）图长方形的面积的比是____．

12．（2022·江苏·苏州市振华中学校七年级期末）10个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个数，并把自己想好的数如实地告诉与他相邻的两个人，然后每个人将与他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报3的人心里想的数是______．



三、解答题
13．（2018·江苏无锡·七年级期末）如图，线段AB=10，动点P从点A出发，以每秒1个单位的速度，沿线段AB向终点B运动，同时，另一个动点Q从点B出发，以每秒3个单位的速度在线段AB上来回运动（从点B向点A运动，到达点A后，立即原速返回，再次到达B点后立即调头向点A运动．） 当点P到达B点时，P，Q两点都停止运动．设点P的运动时间为x．

（1）当x=3时，线段PQ的长为 ．
（2）当P，Q两点第一次重合时，求线段BQ的长．
（3）是否存在某一时刻，使点Q恰好落在线段AP的中点上？若存在，请求出所有满足条件的x的值；若不存在，请说明理由．




14．（2021·江苏·江阴市周庄中学七年级期末）已知点O是直线AB上的一点，∠COE＝90°，OF是∠AOE的平分线．
(1)当点C，E，F在直线AB的同侧(如图1所示)时，试说明∠BOE＝2∠COF；
(2)当点C与点E，F在直线AB的两旁(如图2所示)时，(1)中的结论是否仍然成立?请给出你的结论并说明理由；
(3)将图2中的射线OF绕点O顺时针旋转m°(0＜m＜180°)得射线OD．设∠AOC＝n°，若∠BOD＝(60－n)°，则∠DOE的度数是 (用含n的式子表示)



15．（2021·江苏南通·七年级期末）已知．

（1）如图1，反向延长射线得到射线，用量角器画的平分线．当时，求的度数；
（2）如图2，，用量角器画的角平分线．判断与互为余角吗？说明理由；
（3）利用“备用图”画图研究：画，使与互为补角，进一步画出、的平分线，，并求的度数（若需要，可以用含的式子表示） ．




16．（2019·江苏·苏州市景范中学校七年级期末）如图，点A，B是数轴上的两点．点P从原点出发，以每秒2个单位的速度向点B作匀速运动；同时，点Q也从原点出发用2s到达点A处，并在A处停留1s，然后按原速度向点B运动，速度为每秒4个单位．最终，点Q比点P早3s到达B处．设点P运动的时间为t s．

（1）点A表示的数为_________；当时，P、Q两点之间的距离为________个单位长度；
（2）求点B表示的数；
（3）从P、Q两点同时出发至点P到达点B处的这段时间内，t为何值时，P、Q两点相距3个单位长度？






17．（2021·江苏扬州·七年级期末）已知点A、B、C在数轴上所对应的数分别为a、b、c，b是最大的负整数，且a、b、c满足|4b-a|+（c-5）2=0．
（1）a= ，b= ，c= ；
（2）若在数轴上存在一点P，且PB=2PC，则P点表示的数为 ；
（3）若点A和点C同时分别以每秒4个单位长度和3个单位长度的速度向右运动，同时，点P从原点O以6个单位长度的速度向右运动，设运动的时间为t秒．是否存在常数m，使得4AP+3OC-mOP为定值？若存在，请求出m的值以及这个定值，若不存在，请说明理由．





18．（2021·江苏淮安·七年级期末）定义：对于整数n，在计算n+（n+1）+（n+2）时，结果能被15整除，则称n为15的“亲和数”，如4是15的“亲和数”，因为4+5+6＝15，15能被15整除；﹣7不是15的“亲和数”，因为（﹣7）+（﹣6）+（﹣5）＝﹣18，﹣18不能被15整除．
（1）填空：﹣16　 　15的“亲和数”（填“是”还是“不是”）；
（2）求出1到2021这2021个整数中，是15的“亲和数”的个数；
（3）当n在﹣10到10之间时，直接写出使2n+3是15的“亲和数”的所有n的值．











19．（2021·江苏盐城·七年级期末）已知直线AB和CD交于点O，∠AOC＝α，∠BOE＝90°，OF平分∠AOD．

（1）当α＝30°时，则∠EOC＝_________°；∠FOD＝_________°．
（2）当α＝60°时，射线OE′从OE开始以12°/秒的速度绕点O逆时针转动，同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动，当射线OE′转动一周时射线OF′也停止转动，求经过多少秒射线OE′与射线OF′第一次重合？
（3）在（2）的条件下，射线OE′在转动一周的过程中，当∠E′OF′＝90°时，请直接写出射线OE′转动的时间为_________秒．




20．（2021·江苏泰州·七年级期末）如图，点C在线段AB上，AC＝6cm，CB＝4cm，点M以1cm/s的速度从点A沿线段AC向点C运动；同时点N以2cm/s从点C出发，在线段CB上做来回往返运动（即沿C→B→C→B→…运动），当点M运动到点C时，点M、N都停止运动，设点M运动的时间为ts．
（1）当t＝1时，求MN的长；
（2）当t为何值时，点C为线段MN的中点？
（3）若点P是线段CN的中点，在整个运动过程中，是否存在某个时间段，使PM的长度保持不变？如果存在，求出PM的长度；如果不存在，请说明理由．






21．（2021·江苏盐城·七年级期末）【阅读理解】
射线OC是∠AOB内部的一条射线，若∠COA＝∠BOC，则称射线OC是射线OA在∠AOB内的一条“友好线”．如图1，∠AOB＝60°，∠AOC＝20°，则∠AOC＝∠BOC，所以射线OC是射线OA在∠AOB内的一条“友好线”．
【解决问题】
（1）在图1中，若作∠BOC的平分线OD，则射线OD　 　射线OB在∠AOB内的一条“友好线”；（填“是”或“不是”）
（2）如图2，∠AOB的度数为n，射线OM是射线OB在∠AOB内的一条“友好线”，ON平分∠AOB，则∠MON的度数为 　 　；（用含n的代数式表示）
（3）如图3，射线OB从与射线OA重合的位置出发，绕点O以每秒3°的速度逆时针旋转；同时，射线OC从与射线OA的反向延长线重合的位置出发，绕点O以每秒5°的速度顺时针旋转，当射线OC与射线OA重合时，运动停止．问：当运动时间为多少秒时，射线OA、OB、OC中恰好有一条射线是余下两条射线中某条射线在余下两条射线所组成的角内的一条“友好线”？












22．（2022·江苏宿迁·七年级期末）若A、O、B三点共线，，将一个三角板的直角顶点放在点O处（注：，）．

(1)如图1，使三角板的长直角边OD在射线OB上，则____________°；
(2)将图1中的三角板DOE绕点O以每秒2°的速度按逆时针方向旋转到图2位置，此时，求运动时间的值；
(3)将图2中的三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周，经过秒后，直线OC恰好平分，求的值．

















23．（2022·江苏淮安·七年级期末）
【阅读理解】
射线OC是∠AOB内部的一条射线，若∠AOC＝∠BOC，则称射线OC是射线OA在∠AOB内的一条“友好线”．如图1，若∠AOB＝75°，∠AOC＝25°，则∠AOC＝∠BOC，所以射线OC是射线OA在∠AOB内的一条“友好线”．
【解决问题】
(1)在图1中，若作∠BOC的平分线OD，则射线OD　 　（填“是”或“不是”）射线OB在∠AOB内的一条“友好线”；
(2)如图2，∠AOB的度数为n，射线OM是射线OB在∠AOB内的一条“友好线”，ON平分∠AOB，则∠MON的度数为 　 　（用含n的代数式表示）；
(3)如图3，射线OB先从与射线OA重合的位置出发，绕点O以每秒1°的速度逆时针旋转；10秒后射线OC也从与射线OA重合的位置出发，绕点O以每秒5°的速度逆时针旋转，当射线OC与射线OA的延长线重合时，运动停止．问：当射线OC运动时间为多少秒时，射线OA，OB，OC中恰好有一条射线是余下两条射线中某条射线在余下两条射线所组成的角内的一条“友好线”？




24．（2020·江苏连云港·七年级期末）（1）由大小相同的小立方块搭成的几何体如图1，请在图2的方格中画出该几何体的俯视图和左视图．

（2）用小立方体搭一个几何体，使得它的俯视图和左视图与你在方格中所画的一致，则这样的几何体最少要　　　　个小立方块，最多要　　　　个小立方块．



25．（2022·江苏无锡·七年级期末）近日，无锡市发展改革委印发《关于优化调整居民阶梯气价政策有关事项的通知》，从2022年1月1日起，增加一、二档用气量，“一户多人口”政策同步调整．
气量分档
用气量（立方米）
价格（元/立方米）
调整前
调整后
第一档
年用气量≤300
年用气量≤400
2.73
第二档
300＜年用气量≤600
400＜年用气量≤1000
3.28
第三档
年用气量＞600
年用气量＞1000
3.82
人口超过4人的家庭，每增加1人，一、二档上限增加80立方米、200立方米（原政策一、二档上限增加60立方米、120立方米）．
(1)若小明家有5口人，年用气量1000立方米．则调整前气费为 元，调整后气费为 元；
(2)小红家有4口人，若调整后比调整前气费节省109元，则小红家年用气量为多少立方米？





26．（2022·江苏·苏州市振华中学校七年级期末）定义：当点在线段上，时，我们称为点在线段上的“分值”，记作．
理解：如点是的中点时，即，则，则；反过来，当时，则有．因此我们可以这样理解：“”与“”具有相同的含义．
应用：
(1)如图①，点在线段上．若则__________；若，则__________．


(2)已知线段，点，分别从点、同时出发，相向运动，点到达点时，，都停止运动，设运动时间为．
①若点，的运动速度均为，试用含的式子表示和，并判断它们的数量关系；
②若点和点的运动速度分别为和，点到达点后立即以原速返回，为何值时，．
(3)如图②，在三角形中，，，点，同时从点出发，点沿线段匀速运动至点．点沿线段，匀速运动至点，且点，同时到达点，设．当点运动到线段上时，请用含的式子图②表示．







27．（2022·江苏无锡·七年级期末）甲、乙两家超市新年期间推出优惠活动，推出如表购物优惠方案：
甲超市
乙超市
消费金额（元）
优惠活动
消费金额（元）
优惠活动
0～100（包含100）
无优惠
0～200（包含200）
无优惠
100～350（包含350）
一律享受九折优惠
大于200
超过200元的部分享受八折优惠
大于350
一律享受八折优惠
(1)小王需要购买价格为240元的商品，去哪家店更划算？
(2)小李带了252元去购物、为了买到最多的商品，应选择哪家超市？最多能买到原价为多少元的商品？
(3)小刘在甲超市购物、两次购物分别付了80元和288元，如果小刘把这两次购物改为一次性购物，付款多少元？

















28．（2022·江苏盐城·七年级期末）为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费，该市自来水具体收费价格见下表：
每月用水量
单价（单位：元/m3）
不超过10m3的部分
2
超过10m3，但不超过20m3的部分
4
超过20m3的部分
8
(1)实施“阶梯水价”收费之后，该市一户居民月用水多少立方米时，其当月交费44元？
(2)实施“阶梯水价”收费之后，该市一户居民月用水多少立方米时，其当月的平均水费为每立方米3.2元？





29．（2022·江苏连云港·七年级期末）定义：如果两个一元一次方程的解之和为1，我们就称这两个方程为“美好方程”．例如：方程和为“美好方程”．
(1)若关于x的方程与方程是“美好方程”，求m的值；
(2)若“美好方程”的两个解的差为8，其中一个解为n，求n的值；
(3)若关于x的一元一次方程和是“美好方程，”求关于y的一元一次方程的解．








30．（2022·江苏泰州·七年级期末）对数轴上的点P进行如下操作：将点P沿数轴水平方向，以每秒m个单位长度的速度，向右平移n秒，得到点，称这样的操作为点的“m速移”点称为点的“m速移”点．
(1)点A、B在数轴上对应的数分别是a、b，且．
①若点A向右平移n秒的“5速移”点与点B重合，求n；
②若点A向右平移n秒的“2速移”点与点B向右平移n秒的“1速移”点重合，求n；
(2)数轴上点M表示的数为1，点C向右平移3秒的“2速移”点为点，如果C、M、三点中有一点是另外两点连线的中点，求点C表示的数；
(3)数轴上E，F两点间的距高为3，且点E在点F的左侧，点E向右平移2秒的“x速移”点为点，点F向右平移2秒的“y速移”点为点，如果，请直接用等式表示x，y的数量关系．




















31．（2022·江苏泰州·七年级期末）
(1)如图1：正方形ABCD边长为5，点P、点Q在正方形的边上．点P从点A以每秒3个单位长度的速度沿A→B→C→D→A折线循环运动，同时点Q从点C以每秒1个单位长度的速度沿C→D→A→B→C折线循环运动．
设点P运动时间为x秒．
①当x为何值时，点P和点Q第一次相遇．
②当x为何值时，点P和点Q第二次相遇．
(2)如图2：是长为6，宽为4的长方形ABCD，点E为边CD的中点，点M从点A以每秒2个单位长度的速度沿A→B→C→E折线运动，到达点E停止．设点M运动时间为t秒，当三角形AME的面积等于9时，请求出t的值．




32．（2020·江苏盐城·七年级期末）定义：点C在线段AB上，若BC＝AC，则称点C是线段AB的一个圆周率点．
如图，已知点C是线段AB的一个靠近点A的圆周率点，AC＝3．
（1）AB＝ ；（结果用含的代数式表示）
（2）若点D是线段AB的另一个圆周率点（不同于点C），则CD= ；
（3）若点E在线段AB的延长线上，且点B是线段CE的一个圆周率点．求出BE的长．




33．（2020·江苏镇江·七年级期末）如图，P是线段AB上任一点，AB=12cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2cm/s，D点的运动速度为3cm/s，运动的时间为ts．

（1）若AP=8cm，
①运动1s后，求CD的长；
②当D在线段PB上运动时，试说明AC=2CD；
（2）如果t=2s时，CD=1cm，试探索AP的值．





34．（2022·江苏盐城·七年级期末）阅读探究：，，，…
(1)根据上述规律，小亮发现，求出___________．
(2)小聪继续又发现：

，求出___________．
(3)若，请运用小聪的方法求和的值










35．（2020·江苏苏州·七年级期末）已知有理数a，b在数轴上的位置如图所示．
（1）在数轴上标出﹣a，﹣b的位置，并比较a，b，﹣a，﹣b的大小：
（2）化简|a+b|+|a﹣b|．






36．（2020·江苏·南通市启秀中学七年级期末）数轴上点表示数，点表示数，点表示数，若规定，
（1）当，，时，则______，______．
（2）当，，，时，则______．
（3）当，，且，求的值．
（4）若点、、为数轴上任意三点，，化简：













37．（2022·江苏常州·七年级期末）若x是不等于1的实数，我们把称为x的差倒数，如2的差倒数是，-1的差倒数为，现已知，是的差倒数，是的差倒数，是的差倒数，…，依此类推．
（1）分别求出，，的值；
（2）计算的值；
（3）计算的值．





38．（2020·江苏·扬州市梅岭中学七年级期末）如图，数轴上有点a，b，c三点．

（1）用“