




所属成套资源:【期末·解答题专练】2022-2023学年 人教版数学九年级-期末解答题必刷训练
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题03《判别式及根与系数的关系》期末解答题必刷训练 试卷 4 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题04《二次函数与实际问题》期末解答题必刷训练 试卷 3 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题05《二次函数与几何综合题》期末解答题必刷训练 试卷 6 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题07《统计与概率》期末解答题必刷训练 试卷 4 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题08《期末压轴题(尖子生必练)》期末解答题必刷训练 试卷 9 次下载
【期末·解答题专练】2022-2023学年 人教版数学九年级-专题06《圆》期末解答题必刷训练
展开
这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题06《圆》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题06圆解析版docx、期末解答题专练人教版数学九年级上学期-专题06圆原卷版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
2圆
1.如图,⊙O的直径BE为4,∠BAE的平分线AD交⊙O于点D,交BE于点F,C是BE延长线上一点,且FC=AC.
(1)求BD的长.
(2)求证:AC是⊙O的切线.
【答案】(1);(2)见解析
【分析】
(1)连接OD,根据角平分线的定义和圆周角定理可得∠BOD=2∠BAD=90°,由勾股定理求解即可;
(2)连接OA,根据等腰三角形等边对等角性质可得∠CAF=∠CFA,∠OAF=∠ODF,进而可证明OA⊥AC,根据圆的切线的判定即可证得结论.
【详解】
(1)解:连接OD,
∵⊙O的直径BE为4,
∴∠BAE=90°,BO=OD=2,
∵AD平分∠BAE,
∴∠BOD=2∠BAD=90°,
在Rt△BOD中,由勾股定理得:;
(2)证明:连接OA,
∵FC=AC,OA=OD,
∴∠CAF=∠CFA,∠OAF=∠ODF,
∵∠CFA=∠DFO,∠BOD=90°,
∴∠CAF+∠OAF=∠CFA+∠ODF=∠DFO+∠ODF=90°,
∴∠OAC=90°,即OA⊥AC,
∵OA为⊙O的半径,
∴AC是⊙O的切线.
【点睛】
本题考查圆周角定理、等腰三角形的性质、角平分线的定义、勾股定理、对顶角相等、切线的判定、直角三角形的两锐角互余等知识,解答的关键是熟练掌握相关知识的联系与运用.
2.如图所示,在平面直角坐标系中,⊙P经过原点,交x轴于点A(4,0),交y轴于点B(0,3),点C是劣弧OA的中点,连接BC.
(1)求⊙P的半径
(2)求弦BC的长
【答案】(1);(2)
【分析】
(1)利用A,B点坐标得出AO,BO的长,进而得出AB的长,即可得出圆的半径;
(2)连接PC交OA于点H,连接AC,先根据勾股定理得出PH=,AC=,最后根据勾股定理求出结果.
【详解】
(1)解:∵⊙P过原点O,与x轴交于A(4,0),与y轴交于B(0,3),
∴AB是⊙O的直径,AO=4,BO=3,
由题意可得出:OA2+OB2=AB2,
∴AB=5,
∴⊙P的半径为;
(2)连接PC交OA于点H,连接AC,
∵点C是劣弧OA的中点,
∴OH=AH==2,PH⊥OA,
∵PA=,
∴PH==,
∴CH=PC-PH=-=1,
∴AC=,
∵AB为⊙P的直径,
∴∠ACB=90°,
∴BC==2.
【点睛】
本题考查了垂径定理以及勾股定理等知识,解题的关键是学会添加常用辅助线.
3.已知△ABC内接于⊙O,AB=AC, 点D是⊙O上一点.
(1)如图①,若∠BAC=40°BD为⊙O的直径,连接CD,求∠DBC和∠ACD的大小;
(2)如图②,若CD∥BA,连接AD,延长OC到E,连接DE.使得3∠BAC-∠E=90°,判断DE与⊙O关系并证明.
【答案】(1)50°,20°;(2)DE为⊙O的切线,证明见解析.
【分析】
(1)利用等腰三角形的性质和三角形内角和计算出∠ABC=70°,再根据圆周角定理得到∠BCD=90°,∠D=40°,利用互余计算出∠DBC的度数,利用圆周角定理计算∠ABD的度数,从而得到∠ACD的度数;
(2)连接AO,并延长AO交BC于点F,证明∠OCA=∠OAC=∠BAC,连接OD,证明3∠BAC+∠COD=180︒减去3∠BAC-∠E=90°即可进一步证明结论.
【详解】
解:(1)∵AB=AC,
∴∠ABC=∠ACB=(180°-∠BAC)=×(180°-40°)=70°,
∵BD为直径,
∴∠BCD=90°,
∵∠D=∠BAC=40°,
∴∠DBC=90°-∠D=90°-40°=50°;
∴∠ACD=∠ABD=∠ABC-∠DBC=70°-50°=20°;
(2)DE为⊙O的切线.
证明:如图,连接AO,并延长AO交BC于点F,
∵AB=AC
∴∠FAC=∠BAC
∵OA=OC
∴∠OCA=∠OAC=∠BAC
连接OD,
∵OC=OD
∴∠OCD=∠ODC=∠OCA+∠ACD
∵AB//CD
∴∠ACD=∠BAC
∴∠OCD=∠ODC=
∴∠OCD+∠ODC+∠COD=3∠BAC+∠COD=180︒①
∵3∠BAC-∠E=90°
∴①-②得:∠COD+∠E=90︒
∴∠ODE=90°,即
∴∵DE为⊙O的切线.
【点睛】
本题考查了切线的判定,圆周角定理以及直角三角形的性质,熟练掌握切线的判定定理是解答本题的关键.
4.如图,Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,且E是AB中点,连接OA.
(1)求证:OA=OB;
(2)连接AD,若⊙O的半径为2,求AD.
【答案】(1)见解析;(2).
【分析】
(1)连接OE,根据切线的性质得,则可判断OE垂直平分AB,根据线段垂直平分线的性质即可得出结论;
(2)先证明AO平分,再证明,可得出AC和CD的值,最后根据勾股定理即可得出答案.
【详解】
(1)证明:连接OE,如图:
以CD为直径的⊙O与直线AB相切于点E,
E是AB中点,
OE垂直平分AB
(2)
AO平分
由(1)知,OA=OB
在中,.
【点睛】
本题考查了切线的性质:圆的切线垂直于经过切点的半径,也考查了勾股定理,线段垂直平分线的性质,熟练掌握性质定理是解题的关键.
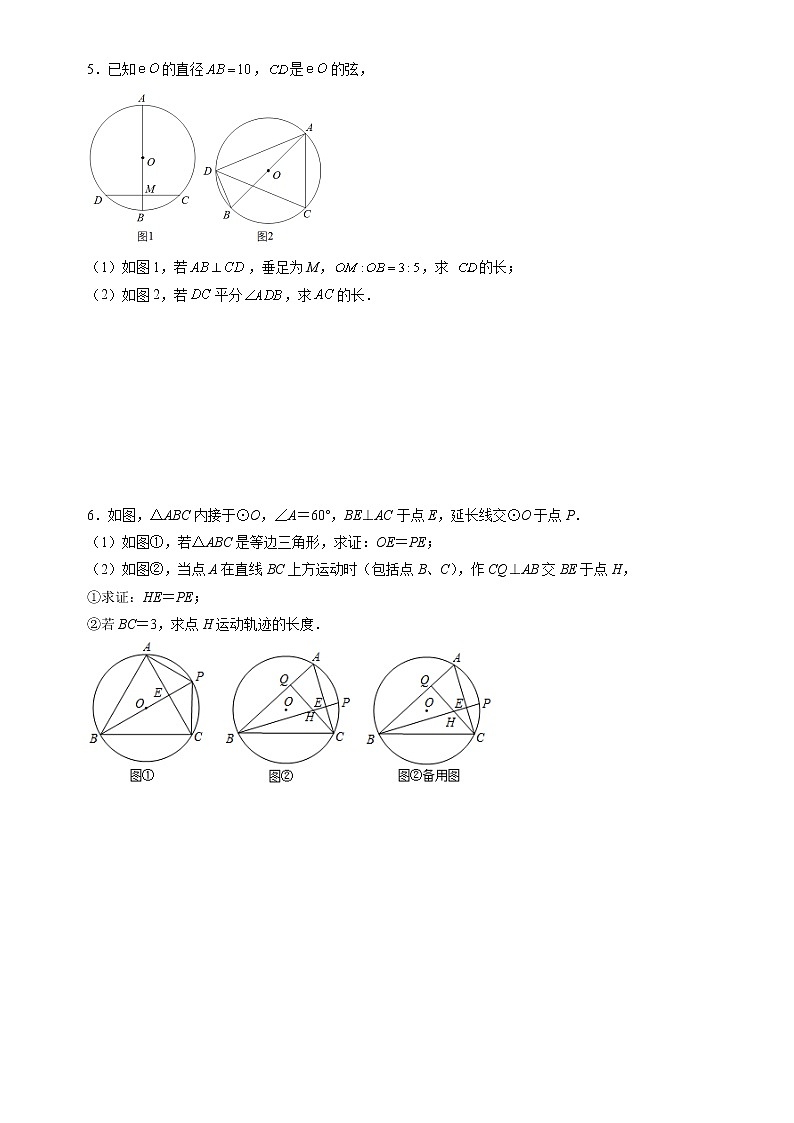
5.已知的直径,是的弦,
(1)如图1,若,垂足为M,,求 的长;
(2)如图2,若平分,求的长.
【答案】(1);(2)
【分析】
(1)根据,求出,连接,利用勾股定理求出,再利用垂径定理求出答案即可;
(2)连接,根据角平分线的性质及同弧所对的圆周角相等证得,推出,利用直径推出,再根据勾股定理得到,由此求出答案.
【详解】
解:(1)∵直径,
∴,
∵,
∴,
连接,
∵,
∴∠,,
∴,
∴,
解得,
∴
(2)连接,
∵平分,
∴,
∴,
∴,
∵是直径,
∴,
∴,
=.
【点睛】
此题考查圆的知识:垂径定理,圆周角定理以及勾股定理和角平分线的性质,熟记圆的基础知识并熟练应用是解题的关键.
6.如图,△ABC内接于⊙O,∠A=60°,BE⊥AC于点E,延长线交⊙O于点P.
(1)如图①,若△ABC是等边三角形,求证:OE=PE;
(2)如图②,当点A在直线BC上方运动时(包括点B、C),作CQ⊥AB交BE于点H,
①求证:HE=PE;
②若BC=3,求点H运动轨迹的长度.
【答案】(1)见解析;(2)①见解析;②
【分析】
(1)由圆周角定理可得∠BPC=∠BAC=60°再由OC=OP,可证△OCP是等边三角形,再由CE⊥OP,即可得到OE=PE;
(2)①连接PC,同理可得∠BPC=∠BAC=60°,然后证明∠ACQ=30°,则可得到∠CHE=60°,可证△CPH是等边三角形,由此即可证明;
②由①得∠CHP=60°,得到∠BHC=120°,则H是在以BC为弦,圆周角∠BHC=120°的圆上运动,由此利用弧长公式求解即可.
【详解】
解:(1)如图所示,连接OC,PC,
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BPC=∠BAC=60°,
∵圆O是△ABC的外接圆,
∴圆O是△ABC三边的垂直平分线的交点,
∵△ABC是等边三角形,BE⊥AC,
∴BE在线段AC的垂直平分线上,
∴O在线段BP上,
∴OC=OP,
∴△OPC是等边三角形,
∵CE⊥OP,
∴OE=PE;
(2)①如图所示,连接PC,
同理可得∠BPC=∠BAC=60°,
∵CQ⊥AB,
∴∠AQC=90°,
∴∠ACQ=30°,
又∵AC⊥BE,
∴∠CEH=90°,
∴∠CHE=60°,
∴△CPH是等边三角形,
∴PE=HE;
②由①得∠CHP=60°,
∴∠BHC=120°,
∵BC=4,
∴H是在以BC为弦,圆周角∠BHC=120°的圆上运动,
如图所示,劣弧即为H的运动轨迹,过点作于G,
∴
∵∠BHC=120°
∴,
∴,
∴∠,
∴,
∵,
∴,
∴,
∴.
【点睛】
本题主要考查了同弧所对的圆周角相等,等边三角形的性质与判定,弧长公式,弧、弦与圆心角的关系,含30度角的直角三角形的性质,弧长公式,解题的关键在于能够熟练掌握等边三角形的性质与判定条件.
7.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点;
(2)若DF=7,AC=24,求⊙O的直径.
【答案】(1)见解析;(2)
【分析】
(1)利用圆周角定理得到∠ACB=90°,再证明OF⊥AC,然后根据垂径定理得到点D为的中点;
(2)设⊙O的半径为R,,连接OC,运用勾股定理求解即可.
【详解】
解:(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴,
即点D为的中点.
(2)连接OC,如图,
设⊙O的半径为R,
∵DF=7
∴OF=R-7
∵AC=24
∴CF=12
在Rt△OCF中,
∴
解得,
∴⊙O的直径=
【点睛】
本题考查了圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.
8.如图,为外接圆⊙O的直径,且与⊙O相切于点.
(1)求证:;
(2)若,,,求⊙O的半径.
【答案】(1)见解析;(2)5
【分析】
(1)连接OA,根据切线的性质得出∠OAB+∠BAE=90°,根据圆周角定理得到∠DAO+∠OAB=90°,∠D=∠C,再推出∠DAO=∠BAE,根据等腰三角形的性质得到∠C=∠DAO,从而推出∠BCA=∠BAE
(2)根据垂径定理求出BF,根据勾股定理求出AF,再根据勾股定理求出OB即可.
【详解】
解:证明:(1)连接OA交BC于点F,
∵AE与⊙O相切于点A,
∴OA⊥AE,即∠OAB+∠BAE=90°,
∵BD为⊙O的直径,
∴∠DAB=∠DAO+∠OAB=90°,
∴∠DAO=∠BAE,
∵OA=OD,
∴∠C=∠DAO,
∵由圆周角定理得:∠D=∠C,
∴∠D=∠DAO,
∴∠DAO=∠BAE,
∴∠BCA=∠BAE;
(2)解:∵AE∥BC,AE⊥OA,
∴OA⊥BC,
∴FB=BC=×8=4,
∴在Rt△ABF中,AF==2,
∵在Rt△OFB中,OB2=BF2+OF2,
∴OB2=42+(0B-2)2,
∴OB=5,
∴⊙O的半径为5.
【点睛】
本题考查了三角形的外接圆与外心,切线的判定,勾股定理,等腰三角形的性质,圆周角定理等知识点,能综合运用知识点进行推理是解此题的关键.
9.如图,中,,,,它的内切圆分别和,,切于点,,,求,和的长.
【答案】AE=4,BD=9,CF=5
【分析】
设AE=x,根据切线长定理得到AF=AE=x,BE=BD=13-x,CD=CF=9-x,则13-x+9-x=14,然后解方程求出x,从而得到AE、BD、CF的长.
【详解】
解:设AE=x,
∵△ABC的内切圆分别和BC,AB,AC切于点D,E,F,
∴AF=AE=x,BE=BD,CD=CF,
而BE=BA-AE=13-x,CF=CA-AF=9-x,
∴BD=13-x,CD=9-x,
而BD+CD=BC,
∴13-x+9-x=14,解得x=4,
∴AE=4,BD=9,CF=5.
【点睛】
本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了切线长定理.
10.如图,在ABC中,线段BC的中点D在以AB为直径的⊙O上,过点D作⊙O的切线DE,交AC于点E,AC的延长线交⊙O于点F.
(1)求证:DE⊥AC.
(2)若DE+EA=4,AF=8.求⊙O的半径.
【答案】(1)见解析;(2)5
【分析】
(1)连接OD,先根据可得,再根据直径的性质可得AD⊥BC,结合点D是BC中点可得,进而可得,由此可证得,最后再结合切线的性质即可得到结论;
(2)过点作于点,于是得到,推出四边形是矩形,根据矩形的性质得到,.由垂径定理得到,设,则,,根据勾股定理列方程即可得到结论.
【详解】
(1)证明:如图,连接OD,
,
,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵点D为BC的中点,
∴,
,
,
∴,
是的切线,
,
;
(2)解:如图,过点作于点,
则,
四边形是矩形,
,,
,
设.
,
,,
∵在中,,
,解得:,
,
的半径为5.
【点睛】
本题考查了切线的性质,等腰三角形的性质,垂直平分线的判定与性质,矩形的判定与性质,垂径定理以及勾股定理的应用等相关知识,熟练掌握相关图形的性质与判定是解决本题的关键.
11.如图,在ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AB=10,∠A=60°,求CD的长.
【答案】(1)见解析;(2)CD 长为5.
【分析】
(1)作辅助线,根据等腰三角形三线合一得BD=CD,根据三角形的中位线可得OD∥AC,所以得OD⊥EF,从而得结论;
(2)根据等腰三角形三线合一的性质证得∠BAD=∠BAC=30°,由30°的直角三角形的性质即可求得BD.
【详解】
(1)证明:连接OD,AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD是△BAC的中位线,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:∵AB=AC,AD⊥BC,
∴∠BAD=∠BAC=30°,
∴CD=BD=AB=×10=5,即CD 长为5.
【点睛】
本题主要考查的是切线的判定和性质,圆周角定理、等腰三角形的性质,30°的直角三角形的性质,掌握本题的辅助线的作法是解题的关键.
12.小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.
(1)更换定理的题设和结论可以得到许多真命题.如图1,在中,是劣弧的中点,直线于点,则.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,,组成的一条折弦.是劣弧的中点,直线于点,则.可以通过延长、相交于点,再连接证明结论成立.请写出证明过程;
(3)如图3,,组成的一条折弦,若是优弧的中点,直线于点,则,与之间存在怎样的数量关系?请写出证明过程.
【答案】(1)见解析;(2)见解析;(3),理由见解析
【分析】
(1)连接,,易证为等腰三角形,根据等腰三角形三线合一这一性质,可以证得.
(2)根据圆内接四边形的性质,先,再证为等腰三角形,进一步证得,从而证得结论.
(3)根据,从而证明,得出,然后判断出,进而求得.
【详解】
证明:(1)如图1,连接,,
是劣弧的中点,
,
,
,
,,
,
为等腰三角形,
,
;
(2)如图2,延长、相交于点,再连接,
是圆内接四边形,
,
是劣弧的中点,
,
,
为等腰三角形,
,,
,
,
(3).
连接,,,、相交于点,
弧弧,
,
,
,,
,
,
,,
,
,,
,
,
.
【点睛】
本题主要考查了垂径定理及其推论,等腰三角形的性质,三角形全等的判定及性质,解题的关键是掌握垂径定理在5个条件中,1.平分弦所对的一条弧;2.平分弦所对的另一条弧;3.平分弦;4.垂直于弦;5.经过圆心(或者说直径).只要具备任意两个条件,就可以推出其他的三个.
13.如图,与的边相切于点,与边交于点过上一点且是的直径.
(1)求证:是的切线;
(2)若,求的长;
(3)在(2)的条件下,求的长.
【答案】(1)见解析;(2);(3)
【分析】
(1)连接,根据切线的性质可得,根据半径相等,等边对等角可得,由平行线的性质可得,进而可得,进而证明,可得即可证明是的切线;
(2)连接,勾股定理求得,设,则,,根据勾股定理列出方程即可求得的长;
(3)连接,,证明,勾股定理求得, 根据,在中,勾股定理即可求得的长.
【详解】
(1)连接,如图,
是的切线
在与中
,
是半径
是的切线;
(2)连接,
,,
在中,
,
设,则,
在中
解得
(3)连接,,
,
中
,
是的直径.
是直角三角形
【点睛】
本题考查了切线的性质与判定,勾股定理,直径所对的圆周角是直角,掌握切线的性质与判定是解题的关键.
14.如图中所示,AB和BC组成圆的折弦,AB>BC,D是的中点,DE⊥AB,垂足为E.连结AD,AC,BD.
(1)写出所有与∠DBA相等的角(不添加任何线段)__________.
(2)判断AE,BE,BC之间的数量关系并证明.
(3)如图,已知AD=7,BD=3,求AB·BC的值.
【答案】(1);(2),见解析;(3)40
【分析】
(1)根据题意可得,根据等弧所对的圆周角相等即可求得;
(2)在线段上截取,根据是的中垂线,,可得,进而可得,;
(3)根据即可求得.
【详解】
(1)是的中点,
故答案为:
(2)
理由如下:如图,在线段上截取,
∵
∴是的中垂线
∴ ,
∵点D是的中点,
∴,,
∴
∵
∴,
∵,
∴ ,
∴,
∴,
∴
即
(3)∵
∴
∴
【点睛】
本题考查了圆周角定理的推论,三角形全等的性质与判定,勾股定理,正确的添加辅助线是解题的关键.
15.如图,O为菱形 ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为1,∠ABC=60°,求⊙O的半径.
【答案】(1)见解析;(2)
【分析】
(1)根据菱形的性质得到AC是角平分线,再根据角平分线的性质进行证明;
(2)根据菱形的边长可以求得其对角线的长,根据等腰直角三角形的性质和对角线的长列方程求解.
【详解】
解:(1)连接OM,过点O作ON⊥CD于N,
∵⊙O与BC相切于点M,
∴OM⊥BC,
∴∠OMC=∠ONC=90°,
∵AC是菱形ABCD的对角线,
∴∠ACB=∠ACD,
∵OC=OC,
∴△OMC≌△ONC,
∴ON=OM,
∴CD与⊙O相切;
(2)∵ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴∠ACB=60°,AC=1,
设半径为r.则OC=1-r,OM=r,
∵∠ACB=60°,∠OMC=90°,
∴∠COM=30°,MC=,
∴
解得r,
∴⊙O的半径为.
【点睛】
此题综合考查了菱形的性质和圆的切线的性质和判定.注意本题中运用数量关系证明圆的切线的方法.
16.如图,⊙O经过菱形ABCD的B,D两顶点,分别交AB,BC,CD,AD于点E,F,G,H.
(1)求证AE=AH;
(2)连接EF,FG,GH,EH,若BD是⊙O的直径,求证:四边形EFGH是矩形.
【答案】(1)见解析;(2)见解析
【分析】
(1)连接DE、BH,根据菱形的性质,证明△ADE≌△ABH即可;
(2)连接DE,DF,根据圆的性质,证明△ADE≌△CDF和△AEH≌△CFG,
后运用有一个角是直角的平行四边形是矩形完成证明.
【详解】
(1)证明:连接DE、BH,
∵四边形ABCD是菱形,
∴AB=AD.
∵∠A=∠A,∠ADE=∠ABH,
∴△ADE≌△ABH.
∵AE=AH.
(2)连接DE,DF.
∵BD是⊙O的直径,
∴∠BED=∠BFD=90°.
∴∠AED=∠CFD=90°.
∵AD=CD,∠A=∠C,
∴△ADE≌△CDF.
∴AE=CF
∵用(1)中同样的方法可证CF=CG
∴AH=CG.
∴△AEH≌△CFG.
∴EH=FG.
∴∠AHE=∠AEH=90°-∠A,∠ADB=∠ABD=90°-∠A,
∴∠AHE=∠ADB
∴EH∥BD
同理可证FG∥BD,
∴EH∥FG
∴四边形EFGH是平行四边形.
∴∠FEH=∠FGH.
又∵四边形EFGH是⊙O的内接四边形,
∴∠FEH+∠FGH=180°,
∴∠FEH=90°,
∴四边形EFGH是矩形.
【点睛】
本题考查了菱形的性质,圆的性质,三角形全等的判定和性质,平行四边形的判定和性质,矩形的判定,熟练菱形的性质,矩形的判定是解题的关键.
17.如图1,在RtΔABC中,∠B=90°,∠C=40°,以AB为直径画⊙O交AC于点D, E是线段AB上的动点,延长DE交⊙O于F点,连接AF.
(1)如图1,求∠F的度数:
(2)如图2,当AE=AD时,求∠DFO的度数.
【答案】(1)40°;(2)15°
【分析】
(1)根据直角三角形的性质先求出∠BAC,连接DO,求出∠AOD,再根据圆周角的性质求出∠F;
(2)连接DO,同(1)先求出∠AFD,根据AE=AD得到∠AED=65°,故可求出∠FAO=25°,根据等腰三角形的性质求出∠AFO,故可得到∠DFO的度数.
【详解】
(1)∵∠B=90°,∠C=40°
∴∠BAC=50°,
连接DO,
∵AO=DO
∴∠ADO=∠BAC=50°,
∴∠AOD=180°-∠ADO-∠BAC=80°
∴∠F=∠AOD=40°;
(2)连接DO,同(1)先求出∠BAC=50°,∠AFD=40°
∵AE=AD
∴∠AED==65°,
∴∠FAO=∠AED-∠AFD=25°,
又AO=FO
∴∠AFO=∠FAO=25°,
∴∠DFO=∠AFD-∠AFO=15°.
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知圆周角的性质、等腰三角形的性质和外角定理的运用.
18.如图,PA是的切线,切点为A,AC是的直径,连接OP交于D.过点C作,连接AB交OP于点E.
(1)求证:PB是的切线;
(2)若E恰好是OD的中点,且四边形OAPB的面积是,求阴影部分的面积;
(3)若且,求AB的长度.
【答案】(1)见解析(2)(3)4
【分析】
(1)连接OB,再证明△AOP≌△BOP,可得结论.
(2)先证明△AOD是等边三角形,设OE=m,用m的代数式表示AB,OP,构建方程求出m,求出OA,AB,OE,再根据S阴=S扇形OAB−S△AOB,求解即可.
(3)在Rt△AOE中,,可以假设OE=x,则OA=OD=3x,DE=2x,AE=,在Rt△ADE中,根据AD2=AE2+DE2,构建方程求出x,故可求解.
【详解】
(1)证明:连接BO,
∵PA是的切线,
∴AP⊥AO,
∴∠PAO=90°
∵,AC是直径
∴∠AEO=∠ABC=90°
∴OP⊥AB,
∴∠AOP=∠BOP
又∵AO=BO,OP=OP
∴△AOP≌△BOP,
∴∠PBO =∠PAO=90°,
∴PB是的切线
(2)解:∵E是OD的中点
∴OE=DE,
∵AB⊥OD,
∴∠AEO=∠AED=90°
又AE=AE
∴△AEO≌△AED(SAS)
∴AO=AD,
∵OA=OD,
∴AD=OA=OD,
∴△AOD是等边三角形,
∴∠AOD=60°,∠OAE=30°
设OE=m,则AO=2m,AE=BE=m,AB=2m,OA=2m,
∵∠APO=90°-∠AOP=30°
∴OP=4m,
∵四边形OAPB的面积是16,
∴•OP•AB=16,
∴×4m×2m=16,
∴m=2或−2(舍弃),
∴OE=2,AB=4,OA=2m=4,
∵OD⊥AB,
∴,
∴∠AOD=∠BOD=60°,
∴∠AOB=2∠AOD=120°,
∴S阴=S扇形OAB−S△AOB=−×4×2=.
(3)解:在Rt△AOE中,,
∴可以假设OE=x,则OA=OD=3x,DE=2x,AE==x,
在Rt△ADE中,AD2=AE2+DE2,
∴()2=(x)2+(2x)2,
∴x=1或−1(舍弃),
∴OE=1,OA=3,AE=,
∴AB=2AE=4.
【点睛】
本题属于圆综合题,考查了切线长定理,垂径定理,勾股定理,等边三角形的判定和性质,四边形的面积等知识,解题的关键是学会利用参数构建方程解决问题.
19.如图,在RtABC中,∠C=90°,BD是ABC的角平分线,点O在AB上,以点O为圆心,OB长为半径的圆经过点D,交BC于点E,交AB于点F.
(1)求证:AC是⊙O的切线;
(2)若CE=2,CD=4,求半径的长.
【答案】(1)见解析;(2)半径的长为5.
【分析】
(1)连接,由为角平分线得到一对角相等,再根据等腰三角形的性质得出一对内错角相等,进而确定出与平行,利用两直线平行同位角相等得到为直角,由此即可得证;
(2)过作垂直于,可得出四边形为矩形,由此可得OG=CD=4,设OE=OD=CG=x,利用勾股定理列出方程即可求得答案.
【详解】
(1)证明:如图,连接,
为的平分线,
,
,
,
,
∴,
,
,
是的切线;
(2)解:过作,连接,
∵,,
∴四边形为矩形,
∴,,
设OE=OD=CG=x,则GE=CG-CE=x-2,
∵在中,,
∴,
解得:,
∴,
即半径的长为5.
【点睛】
此题考查了切线的判定,等腰三角形的性质,矩形的判定与性质,平行线的判定与性质以及勾股定理等知识,熟练掌握切线的判定方法是解本题的关键.
20.如图,在中,直径与弦相交于点, .
(1)如图①,若,求和∠CDB的大小;
(2)如图②,若 ,过点D作的切线DF ,与AB的延长线相交于点 .求∠ F 的大小.
【答案】(1)27°,32°;(2)26°
【分析】
(1)先求出∠BAD=∠C=27° ,再求出∠ADB=90°,最后计算求解即可;
(2)先求出 ∠AEC=90° ,得到∠A及∠DOB的度数,根据切线的性质得到∠ODF=90°,计算求解即可.
【详解】
解:(1)∵,,
∴∠C=∠AEC-∠ABC=27°,
∴∠BAD=∠C=27°.
∵直径AB与弦CD相交于点E,
∴∠ADB=90°,
又∵∠ABC=∠ADC=58° ,
∴∠CDB=∠ADB-∠ADC=32°.
(2)∵,
∴∠AEC=90°.
又∵∠ABC=∠ADC=58°,
∴∠A=90°-∠ADC=32°.
∴∠DOB=2∠A=64°.
∵DF是的切线,
∴∠ODF=90° .
∴∠F=90°-64°=26°.
【点睛】
此题考查同弧所对的圆周角相等的性质,垂线的定义,切线的性质,三角形外角的性质,直径所对的圆周角是直角的性质,熟记各知识点并熟练应用是解题的关键.
21.如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=5,半径为2的⊙O分别与AC、BC相切于点E、F.
(1)求证:AB是⊙O的切线;
(2)求图中阴影部分的面积.
【答案】(1)见解析;(1)
【分析】
(1)连接OE、OF、OC,作OM⊥AB,垂足为M,利用面积法求出OM的长,由此得到结论;
(2)先证明OA、OB分别是∠CAB、∠CBA的角平分线,得到∠AOB=135º,再利用扇形面积公式计算即可得到答案.
【详解】
(1)连接OE、OF、OC,作OM⊥AB,垂足为M,
∵⊙O与AC,BC相切,
∴OE=OF=2,∠OEC=∠OFC=90°,
∵AC=12,BC=5,
∴AB=13,
由面积法S△AOC+S△BOC+S△AOB=S△ABC,
∴OE·AC+OF·BC+OM·AB=AC·BC,
∴OM=2,
又∵OM⊥AB,
∴AB是⊙O的切线;
(2)OM⊥AB,∠OEC=∠OFC=90º,OE=OF=OM,
∴OA、OB分别是∠CAB、∠CBA的角平分线,
由∠ACB=90°,∴∠CAB+∠CBA=90°,
∴∠OAB+∠OBA=45°,∠AOB=135º,
∴S阴影=S△AOB-S扇形=×13×2-×π×22=.
【点睛】
此题考查切线的判定定理和性质定理,角平分线的性质,正确掌握面积法计算三角形的面积,由此求线段长度是解题的关键.
22.如图,AB是⊙O的直径,C是⊙O上一点,连接BC,过O点作OD⊥BC于D点,交弧BC于E点,连接AE交BC于F点.
(1)如图1,求证:∠BAC=2∠E;
(2)如图2,连接OF,若OF⊥AB,DF=1,求AE的长.
【答案】(1)见解析;(2)6
【分析】
(1)根据垂径定理可知,,进而可得,由可得,进而即可证明;
(2)由是直径,可得,根据,可得,进而可得,根据含30度角的直角三角形的性质即可求得,进而求得的长.
【详解】
(1)
,
,
(2)是直径
又
在中,
【点睛】
本题考查了垂径定理,等弧所对的圆周角相等,垂直平分线的定理,等边对等角,含30度角的直角三角形的性质,直径所对的圆周角是直角,求得是解题的关键.
23.如图,四边形ABCD内接于⊙O,AC为直径,BD=DC,过C作CG⊥BD于E,交AB于F,交DA的延长线于点G,
(1)求证:AG=FG;
(2)若DH⊥AC于H,AH=,AB=6,求HC的长度.
【答案】(1)证明见祥解;(2)HC= 6+.
【分析】
(1)由BD=DC,可得∠DBC=∠DCB,由四边形ABCD内接于⊙O,可得∠DCB=∠GAF,根据AC为直径, CG⊥BD,可得∠EFB=∠EBC,进而可得∠GFA∠GAF即可;
(2)过D作DJ⊥BC,根据等腰三角形性质BD=DC,DJ⊥BC,BJ=CJ,根据垂径定理可得DJ过圆心O,可证OJ为△ABC的中位线,OJ=AB=,再证△DOH≌△COJ(AAS),OH=OJ=3即可.
【详解】
(1)证明:∵BD=DC,
∴∠DBC=∠DCB,
∵四边形ABCD内接于⊙O,
∴∠DCB+∠DAB=180°,∠GAF+∠DAB=180°,
∴∠DCB=∠GAF,
∵AC为直径, CG⊥BD,
∴∠ABC=90°,∠FEB=90°
∴∠EFB+∠EBF=∠EBF+∠EBC=90°,
∴∠EFB=∠EBC,
∴∠GFA=∠EFB=∠EBC=∠DCB=∠GAF,
∴AG=FG;
(2)解:过D作DJ⊥BC,
∵BD=DC,DJ⊥BC,
∴BJ=CJ,DJ过圆心O,
∵OA=OC,AB=6,
∴OJ为△ABC的中位线,
∴OJ=AB
∵DH⊥AC,DJ⊥BC,
∴∠DHO=∠CJO=90°,
,在△DOH和△COJ中,
,
△DOH≌△COJ(AAS),
∴OH=OJ=3
∵AH=,
∴AO=AH+HO=+3,
∴HC=HO+OC=HO+OA=3++3=6+,
【点睛】
本题考查等腰三角形的判定与性质,圆内接四边形的性质,同角的余角性质,三角形中位线性质,三角形全等判定与性质,本题综合较强,难度较大,利用辅助线画出准确图形,掌握相关知识是解题关键.
24.如图,从外一点引圆的切线,切点为,连接并延长交圆于点,连接.若,
(1)求的度数.
(2)若,求的长.
【答案】(1);(2)
【分析】
(1)连接OB,根据切线的性质,得∠OBA=90°,又∠A=30°,所以∠AOB=60°,再用三角形的外角性质可以求出∠ACB的度数.
(2)设OB=x,则OA=2x,根据勾股定理得出求解即可.
【详解】
解:如图:连接OB,
∵AB切⊙O于点B,
∴∠OBA=90°,
∵∠A=30°,
∴∠AOB=90°-30°=60°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠ACB,
∴∠ACB=30°.
(2)由(1)得∠OBA=90°,∵∠A=30°,,
设OB=x,则OA=2x,
∴即,解得(舍去),
∴OB=OC=1,OA=2,
∴AC=OA+OC=2+1=3.
【点睛】
本题考查的是切线的性质,直角三角形的性质,利用切线的性质,结合三角形内角和求出角的度数.
25.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若,CF=2,求⊙O的半径.
【答案】(1)见解析;(2)5
【分析】
(1)连接,由切线的性质和已知条件可证得,则可证得结论;
(2)过作于点,连接,则可证得、,则可求得的长,可求得圆的半径.
【详解】
(1)证明:如图1,连接,
是的切线,且点在上,
,
,
,
平分,
,
,
,
;
(2)解:如图2,过作于点,连接,
,,,
,,
在和中
,
同理可得,
,,
,
的半径.
【点睛】
本题主要考查切线的性质及圆周角定理,解题的关键是掌握过切点的半径与切线垂直,注意全等三角形的应用.
26.如图,AB为的直径,C为上一点,的切线BD交OC的延长线于点D.
(1)求证:;
(2)若,.求CD的长.
【答案】(1)见解析;(2)CD=
【分析】
(1)根据切线的性质得到∠OBD=∠OBC+∠DBC=90°,再根据圆周角定理得到∠ACB=∠OCA+∠OCB=90°,加上∠OBC=∠OCB,于是利用等量代换得到结论;
(2)利用含30度的直角三角形三边的关系得到CB=,然后证明∠D=∠CBD=30°得到CD=CB即可.
【详解】
(1)证明:∵DB是⊙O的切线,
∴BD⊥AB,
∴∠OBD=∠OBC+∠DBC=90°.
∵AB是⊙O的直径,
∴∠ACB=∠OCA+∠OCB=90°.
∵OC=OB,
∴∠OBC=∠OCB.
∴∠DBC=∠OCA;
(2)解:在Rt△ACB中,∵∠A=30°,AC=2,
设,则,
∴,
解得:,
则,
∵∠A=30°,
∴∠COB=2∠A=60°,
∴∠D=90°−∠COB=30°,
∵OA=OC,
∴∠OCA=∠A=30°.
∴∠DBC=∠OCA=30°,
∴∠D=∠DBC.
∴CB=CD.
∴CD=.
【点睛】
本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.
27.如图,⊙O是ABC的外接圆,∠ABC=45°,OCAD,AD交BC的延长线于D,AB交OC于E.
(1)求证:AD是⊙O的切线;
(2)若AE=2,CE=2,求⊙O的半径和线段BE的长.
【答案】(1)见解析;(2)半径为4,
【分析】
(1)连接OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出然后根据勾股定理计算出AH=,则HE=AE-AH=,再利用BE=BH-HE进行计算.
【详解】
解:(1)证明:连接OA,如图,
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC,
∴OA⊥AD,
∵OA是⊙O的半径,
∴AD是⊙O的切线
(2)解:设⊙O的半径为R,则OA=R,OE=R-2,AE=2,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R-2)2=(2)2,解得R=4,
作OH⊥AB于H,如图,OE=OC-CE=4-2=2,
则AH=BH,
∵OH•AE=•OE•OA,
∴
在Rt△AOH中,,
∴
∴,
∴.
【点睛】
本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.经过切点且垂直于切线的直线必经过圆心.也考查了圆周角定理、垂径定理和勾股定理.
28.已知:点P在⊙O外,点A在⊙O上,AB⊥PO于点C,交⊙O于点B,连接PA、PB.
(1)如图1,求证:PA=PB;
(2)如图2,连接OB,设线段PO交⊙O于点E,点D在线段PE上,连接AD,交⊙O于点F,若∠ADO=2∠ABO,求证:AD=OD;
(3)如图3,在(2)的条件下,若PB为⊙O的切线,CO=2DF,AB=4,求⊙O的半径.
【答案】(1)证明见解析;(2)证明见解析;(3)⊙O的半径为.
【分析】
(1)根据垂径定理可得AC=BC,再根据垂直平分线的性质定理即可证明PA=PB;
(2)连接AO,作∠ADO的平分线交OA于G,可证△AGD≌△OGD即可证明结论;
(3)连接OF,OA,作OH⊥AD,交AD于H,可证△AHO≌△OCA,即可用OF表示AD,DC,在Rt△ADC中,根据勾股定理,求得OF,继而求得OC,在Rt△ACO中,根据勾股定理,求得AO即为半径.
【详解】
解:(1)证明:∵AB⊥PO于点C,
∴AC=BC,
∴PA=PB;
(2)如下图,连接AO,作∠ADO的平分线交OA于G,
∵AB⊥PO,
∴∠ACO=90°,
∵AO=OB,
∴∠OAB=∠ABO,
∵∠ADO=2∠ABO,DG为角平分线,
∴∠ADG=∠GDO=∠OAB,
∵∠AOC=∠DOG,
∴∠DGA=∠DGO=∠ACO=90°,
在△AGD和△OGD中
∵∠DGA=∠DGO,DG=DG,∠ADG=∠GDO,
∴△AGD≌△OGD(ASA),
∴AD=OD;
(3)连接OF,OA,作OH⊥AD,交AD于H,
∵OH⊥AD,
∴AH=FH,∠AHO=90°,
∵AD=OD,
∴∠HAO=∠AOC,
在△AHO和△OCA中
∵∠AHO=∠ACO=90°,∠HAO=∠AOC,OA=AO,
∴△AHO≌△OCA,
∴AH=FH=OC,
∵CO=2DF,
∴AD=5DF,DC=DO-OC=AD-OC=3DF,
∵AB=4,
∴AC=BC=2,
在Rt△ADC中,根据勾股定理,
,即,解得,
∴,
在Rt△ACO中,根据勾股定理,
,即,解得,即⊙O的半径为.
【点睛】
本题为圆的综合题,主要考查垂径定理,等腰三角形的性质和判定,勾股定理,全等三角形的性质和判定,垂直平分线的性质定理等.(1)中理解垂直平分线上的点到线段两端距离相等是解题关键;(2)中正确作出辅助线,构造全等三角形是解题关键;(3)中能正确表示直角三角形的三边是解题关键.
29.如图,AB是⊙O直径,点C是⊙O上一点,过点C作⊙O的切线CG,过点B作CG的垂线,垂足为点D,交⊙O于点E,连接CB.
(1)求证:CB平分∠ABD;
(2)若BC=5,BD=3,求AB长.
【答案】(1)证明见解析;(2)
【分析】
(1)连接,根据切线的性质,得,从而得;根据平行线性质,得;根据圆和等腰三角形性质,得,从而完成证明;
(2)连接,过点作于点,根据矩形性质,推导得,;根据勾股定理,计算得;设,通过列方程并求解,即可得,从而得到答案.
【详解】
(1)连接,如下图:
∵CG是⊙O的切线
∴
根据题意,
∴
∴
∵AB是⊙O直径
∴
∴
∴
∴CB平分∠ABD;
(2)连接,过点作于点,如下图:
∴
∵
∴,
∵,
∴四边形为矩形
∴,
∵,BC=5,BD=3
∴
∴
设,则
∵
∴
∴
∴
∴.
【点睛】
本题考查了圆、角平分线、平行线、等腰三角形、矩形、勾股定理、一元一次方程的知识;解题的关键是熟练掌握圆的对称性、切线、勾股定理、矩形的性质,从而完成求解.
30.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,BM平分∠ABC交AC于点D,连结MA,MC.
(1)求证:AMC是正三角形;
(2)若AC=,求⊙O半径的长.
【答案】(1)见解析;(2)2
【分析】
(1)根据角平分线的定义可得∠ABM=∠MBC=60°,再根据同弧所对圆周角相等可得∠MAC=∠ACM=60°,由此即可证得结论;
(2)连接、,过作于点,由圆内接四边形的性质求得,再求得,最后根据30°的直角三角形的性质以及勾股定理即可求得答案.
【详解】
(1)证明:∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠MBC=∠ABC=60°,
∵∠ABM与∠ACM都是弧AM所对的圆周角,
∴∠ACM=∠ABM=60°,
∵∠MAC与∠MBC都是弧MC所对的圆周角,
∴∠MAC=∠MBC=60°,
∴∠MAC=∠ACM=60°,
∴MA=CM,
又∵∠ACM=60°,
∴AMC是正三角形;
(2)解:连接、,过点作于点,如图1,
,
,
,
∵=,
,
∵,,
,
∵,,
,
设,则,
在中,,
∴,
解得:(舍负),
,
∴的半径为2.
【点睛】
本题是主要考查圆周角定理,垂径定理,角平分线定义,等腰三角形的性质,等边三角形的判定,含30°的直角三角形的性质以及勾股定理等相关知识,内容较多,有一定难度,能够灵活运用相关知识是解决本题的关键.
31.在菱形ABCD中,BD=12,∠DBC=30°,点P在对角线上运动,设BP=x,⊙O为△ABP的外接圆.
(1)如图1,当x= ,圆心O落在AB上?
(2)如图2,当PA=PB时,
①判断此时⊙O与BC的位置关系,并说明理由.
②求出x的值.
【答案】(1)6;(2)①⊙O与BC的位置关系相切,理由见解析;②x的值为4;
【分析】
(1)连接AP,当点O在AB上时,AB为圆O直径,∠APB=90°,P为BD中点,x=6.
(2)①连接AP、OP、OB,通过AP=BP得到AB⊥OP推出∠OBP=∠OPB=60°,即可得到∠OBC=∠OBP+∠DBC=90°,得出⊙O与BC的位置关系相切;
②连接AC,得AC⊥BD,BM==6,利用三角比先后求出AM =,AP=4即可得出BP=AP=4
【详解】
(1)连接AP
当点O在AB上时,AB为圆O直径
∴∠APB=90°
∵菱形ABCD中,AB=AD
∴BP=PD= =6
即x=6
(2)①连接AP、OP、OB,
∵AP=BP
∴弧AP=弧BP
∴AB⊥OP
∴∠ABP+∠OPB=90°,
∵菱形ABCD中, ∠ABP=∠DBC=30°
∴∠OPB=60°
又OP=OB
∴∠OBP=∠OPB=60°
∴∠OBC=∠OBP+∠DBC=90°
∴⊙O与BC的位置关系相切
②连接AC,交BD于M,
则AC⊥BD,BM==6
∵tan∠ABP=
∴AM= tan∠ABP×BM=
∵∠APM=∠ABP+∠PAB=60°,sin∠APM=
∴AP==4
∴BP=AP=4
∴x=4
【点睛】
本题考查了圆的垂径定理、直径所对的圆周角是直角、切线的判定以及菱形的性质,数形结合能灵活运用这些知识是解题的关键.
相关试卷
这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题08《期末压轴题(尖子生必练)》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题08期末压轴题尖子生必练解析版docx、期末解答题专练人教版数学九年级上学期-专题08期末压轴题尖子生必练原卷版docx等2份试卷配套教学资源,其中试卷共79页, 欢迎下载使用。
这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题07《统计与概率》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题07统计与概率解析版docx、期末解答题专练人教版数学九年级上学期-专题07统计与概率原卷版docx等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。
这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题05《二次函数与几何综合题》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题05二次函数与几何综合题解析版docx、期末解答题专练人教版数学九年级上学期-专题05二次函数与几何综合题原卷版docx等2份试卷配套教学资源,其中试卷共110页, 欢迎下载使用。









