




- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题03《判别式及根与系数的关系》期末解答题必刷训练 试卷 4 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题04《二次函数与实际问题》期末解答题必刷训练 试卷 3 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题05《二次函数与几何综合题》期末解答题必刷训练 试卷 5 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题06《圆》期末解答题必刷训练 试卷 5 次下载
- 【期末·解答题专练】2022-2023学年 人教版数学九年级-专题07《统计与概率》期末解答题必刷训练 试卷 4 次下载
【期末·解答题专练】2022-2023学年 人教版数学九年级-专题08《期末压轴题(尖子生必练)》期末解答题必刷训练
展开人教版九上期末压轴题(尖子生必练)
1.如图,在半面直角坐标系中,抛物线与x轴交于点A、B,其中点A的坐标为,与y轴交于点.
(1)求抛物线的解析式;
(2)若点D为抛物线上上方的一个动点,过点D作轴,交于点E,过D作,交直线于点F,以、为边作矩形,设矩形的周长为l,求l的最大值;
(3)点P是x轴上一动点,将线段绕点P旋转得到,当点Q刚好落在抛物线上时,请直接写出点Q的坐标.
2.如图,抛物线交x轴于两点,交y轴于点C,点Q为线段上的动点.
(1)求抛物线的解析式;
(2)求的最小值;
(3)过点Q作交抛物线的第四象限部分于点P,连接,记与的面积分别为,设,当S最大时,求点P的坐标,并求S的最大值.
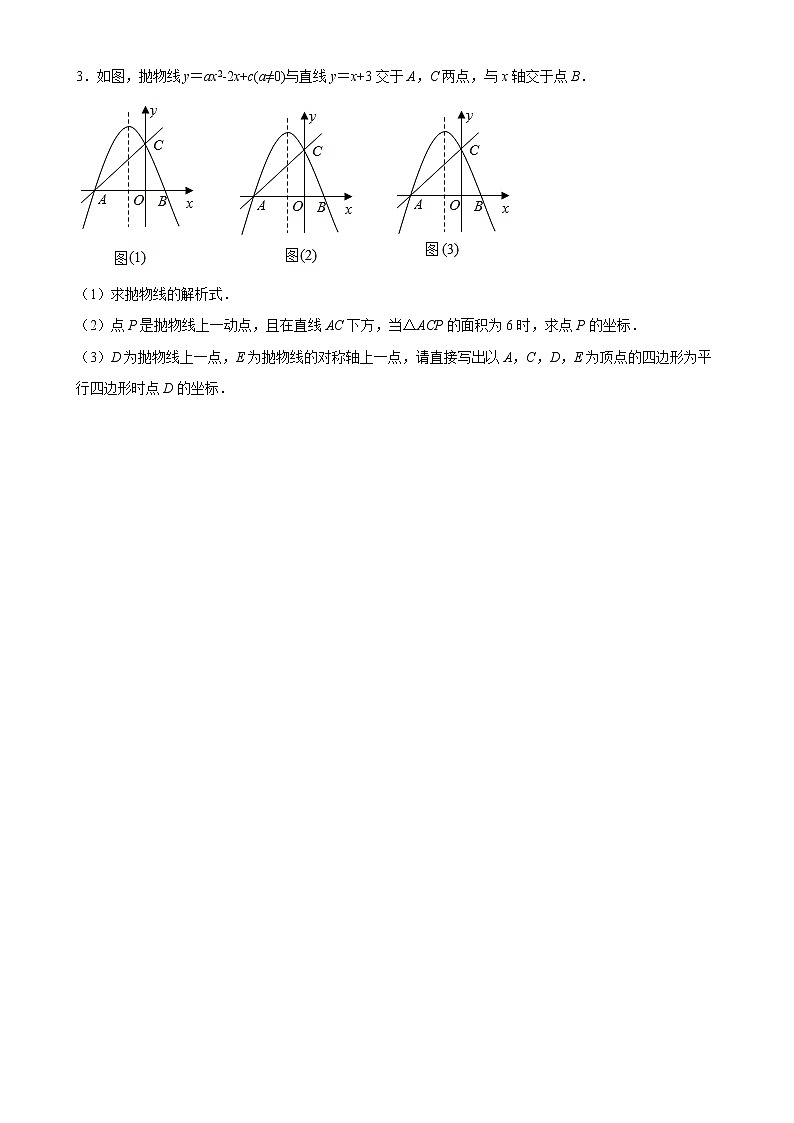
3.如图,抛物线y=ax2-2x+c(a≠0)与直线y=x+3交于A,C两点,与x轴交于点B.
(1)求抛物线的解析式.
(2)点P是抛物线上一动点,且在直线AC下方,当△ACP的面积为6时,求点P的坐标.
(3)D为抛物线上一点,E为抛物线的对称轴上一点,请直接写出以A,C,D,E为顶点的四边形为平行四边形时点D的坐标.
4.已知,平面直角坐标系中,抛物线交y轴于点A,交x轴于点B、C,为等边三角形,.
(1)如图1,求抛物线解析式.
(2)如图2,P为AC上方抛物线上一点,过P作交AC于D,设点P的横坐标为t,PD的长度为d,求d与t的函数关系式;
(3)如图3,在(2)的条件下,在x轴上点B左侧取一点E,使得点E在AD的垂直平分线上,连接ED,若的周长为36,求d的值.
5.如图,抛物线与x轴交于A(2,0),B(-1,0)两点,与y轴交于点C,连接BC,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式;
(2)当线段DF的长度最大时,求D点的坐标;
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.
6.如图,抛物线的对称轴为直线,且抛物线经过两点,与x轴交于点N.
(1)点N的坐标为_______.
(2)已知抛物线与抛物线C关于y轴对称,且抛物线与x轴交于点(点A在点的左边).
①抛物线的解析式为_________;
②当抛物线和抛物线C上y都随x的增大而增大时,请直接写出此时x的取值范围.
(3)若抛物线的解析式为,抛物线的顶点为,与x轴的交点为(点A在点的左边).
①求的值;
②判断抛物线的顶点是否在一条直线上,若在,请直接写出该直线的解析式;若不在,请说明理由.
7.综合与探究
如图1所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A,C.
(1)求抛物线的解析式;
(2)点E在抛物线的对称轴上,求CE+OE的最小值为______.
(3)如图2所示,M是线段OA的上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
①当面积最大时的P点坐标为______;最大面积为______.
②点F是直线AC上一个动点,在坐标平面内是否存在点D,使以点D、F、B、C为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
8.如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示).
(2)若以AD为直径的圆经过点C.
①求a的值.
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
9.已知抛物线与轴交于A,B(点A在点B左侧),与y轴交于C.
(1)求A、B、C的坐标;
(2)点E是抛物线在第二象限内的一动点,当四边形AECB面积最大时,求E点坐标和四边形AECB面积的最大值;
(3)设M在线段AB上且在对称轴左侧,过M作MP⊥x轴交抛物线于P,过P作PQAB交抛物线于Q,过Q作QN⊥x轴于N,如图(2),当矩形MPQN周长最大时,求M的坐标.
10.如图,抛物线y=ax2+bx+c与x轴的两个交点为A、B,且当x<﹣1时,y随x的增大而减小,x>﹣1时,y随x的增大而增大,其最小值为﹣,其图象与x轴的交点B的横坐标是1,过点B的直线l:y=kx+分别与y轴及抛物线交于点C,D.
(1)求直线l和抛物线的解析式;
(2)过点D作x轴的平行线交抛物线于点E,点P是直线DE上的一个动点,点D关于直线OP的对称点F恰好在y轴上,求直线OP的解析式.
(3)将(1)中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方图象的其余部分保持不变,翻折后的图象与原图象x轴上方的部分组成一个“W”形状的新图象,将直线平移得到直线l,若直线l与该新图象恰好有三个公共点,请求出上下平移了几个单位长度.
11.直线与x轴相交于点A,与y轴相交于点B,抛物线经过点A,B,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,若点P为直线上方的抛物线上的一动点,求四边形的面积的最大值;
(3)如图2,为抛物线上的一点,直线与相交于点M,点H在抛物线上,过H作轴,交直线于点K.P是平面内一点,当以点M,H,K,P为顶点的四边形是正方形时,请直接写出点P的坐标.
12.如图,抛物线 y=ax2+bx+3经过A(1,0)、B(4,0)两点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)若点Q是直线x=2上的一个动点,是否存在点Q,使△ACQ为等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
13.已知:如图1,在平面直角坐标系中,⊙P的圆心,半径为5,⊙P与抛物线的交点A、B、C刚好落在坐标轴上.
(1)求抛物线的解析式;
(2)点D为抛物线的顶点,经过C、D的直线是否与⊙P相切?若相切,请证明;若不相切,请说明理由:
(3)如图2,点F是点C关于对称轴的对称点,若直线交y轴于点K,点G为直线上的一动点,则x轴上是否存在一点H,使C、G、H、K四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由.
14.如图,抛物线y=x2+bx+c分别与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C,点P(m,0)为线段OB上(不含端点)的动点,过点P作x轴的垂线交抛物线于点K,交直线BC于点J.
(1)求抛物线的函数解析式;
(2)当PJ:JK=1:2时,求m的值;
(3)点Q是直线BC上的一个动点,将点Q向右平移5个单位长度得到点T,若线段QT与抛物线只有一个公共点,请直接写出点Q的横坐标n的取值范围.
15.某数学活动小组在一次活动中,对一个数学问题作如下探究:
(问题发现)
(1)如图1,正方形ABCD的四个顶点在⊙O上,点E在弧AB上,连结AE、BE、DE.若在DE上截取一点F,使得DF=BE:连结AF,发现△ADF与△ABE全等,请说明理由.
(变式探究)
(2)如图2,正方形ABCD的四个顶点在⊙O上,若点E在弧AD上,过点A作AG⊥BE,探究线段BE、DE、AG之间是否满足BE﹣DE=2AG的关系,请说明理由.
(结论运用)
(3)如图3,在正方形ABCD中,AB=2,若一点P满足PD=2,并且∠BPD=90°,请直接写出点A到BP的距离.
16.(发现问题)爱好数学的小明在做作业时碰到这样一道题:如图1,圆O的半径为2,OA=4,动点B在圆O上,连接AB,作等边三角形ABC(A、B、C为顺时针顺序),求OC的最大值.
(解决问题)小明经过多次的尝试和探索,终于得到解题思路:在图1中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE;
(1)请你找出图中与OC相等的线段,并说明理由;
(2)请直接写出线段OC的最大值
(迁移拓展)
(3)如图2,BC=,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.
17.“数学建模”是中学数学的核心素养,平时学习过程中能归纳一些几何模型,解决几何问题就能起到事半功倍的作用.
(1)如图1,正方形中,,且,求证:;
(2)如图2,正方形中,,延长交的延长线于点,(1)中的结论还成立吗?请说明理由;
(3)如图3在(2)的条件下,作,垂足为点,交于点,连结,求证:.
18.在⊙O中,CD为弦,OP为⊙O的半径,OP交CD于点H,若弧PC=弧PD.
(1)如图1:求证:CD⊥OP;
(2)如图2:直径AB∥CD,弦BE⊥OD于F.求证:BE=2OH;
(3)如图3:在(2)的条件下,连接EC,过C作CN⊥CE交⊙O于N,交AB于M,若PH=AM,OF=4,求线段CN的长.
19.内接于,点在边上,射线交于点,点在弧上,连接,.
(1)如图1,求证:;
(2)如图2,交弦于点,经过点,,求证:;
(3)如图3,在(2)的条件下,为的中点,连接、,若,,求线段的长.
20.如图,AB是⊙O的直径,C、D是⊙O上两点.AE与过点C的切线垂直,垂足为E,直线EC与直径AB的延长线相交于点P,弦CD交AB于点F,连接AC、AD、BC、BD.
(1)若∠ABC=∠ABD=60°,判断△ACD的形状,并证明你的结论;
(2)若CD平分∠ACB,求证:PC=PF;
(3)在(2)的条件下,若AD=5,PF=5,求由线段PC、和线段BP所围成的图形(阴影部分)的面积.
【期末·解答题专练】2022-2023学年 人教版数学九年级-专题07《统计与概率》期末解答题必刷训练: 这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题07《统计与概率》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题07统计与概率解析版docx、期末解答题专练人教版数学九年级上学期-专题07统计与概率原卷版docx等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。
【期末·解答题专练】2022-2023学年 人教版数学九年级-专题06《圆》期末解答题必刷训练: 这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题06《圆》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题06圆解析版docx、期末解答题专练人教版数学九年级上学期-专题06圆原卷版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
【期末·解答题专练】2022-2023学年 人教版数学九年级-专题05《二次函数与几何综合题》期末解答题必刷训练: 这是一份【期末·解答题专练】2022-2023学年 人教版数学九年级-专题05《二次函数与几何综合题》期末解答题必刷训练,文件包含期末解答题专练人教版数学九年级上学期-专题05二次函数与几何综合题解析版docx、期末解答题专练人教版数学九年级上学期-专题05二次函数与几何综合题原卷版docx等2份试卷配套教学资源,其中试卷共110页, 欢迎下载使用。












