




所属成套资源:【期末必刷题】2022-2023学年苏科版数学八年级上册期末考点必刷200题
- 【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练01 选择题-基础(30题) 试卷 1 次下载
- 【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练02 选择题-提升(20题) 试卷 2 次下载
- 【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练04 填空题-基础(30题) 试卷 1 次下载
- 【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练05 填空题-提升(20题) 试卷 2 次下载
- 【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练06 填空题-压轴(15题) 试卷 1 次下载
【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练03 选择题-压轴(15题)
展开
这是一份【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练03 选择题-压轴(15题),文件包含期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练03选择题-压轴15题解析版docx、期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练03选择题-压轴15题原卷版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
专练03 选择题-压轴(15题)
1.(2021·辽宁大石桥·八年级期末)如图,D为的外角平分线上一点并且满足,过D作于E,交BA的延长线于F,则下列结论:
①,②,③,④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
∵AD平分∠CAF,DE⊥AC,DF⊥AB
∴DE=DF
在Rt△CDE和Rt△BDF中
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF
在Rt△ADE和Rt△ADF中
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF
∴∠DBF=∠DCE
∵∠AOB=∠COD(设AC交BD于点O)
∴∠BDC=∠BAC,故③正确;
∵∠BAC+∠ABC+∠ACB=180°
∠BDC+∠DBC+∠DCB=180°
∠DBF=∠DCE
∴∠DAE=∠CBD,
∵∠DAE=∠DAF,
∴∠DAF=∠CBD,故④正确;
综上所述,正确的结论有①②③④.
故选D
【点睛】
本题考查了角平分线上的点到角的两边距离相等的性质、全等三角形的判定与性质,熟记性质并准确识图判断出全等的三角形是解题的关键,难点在于需要二次证明三角形全等.
2.(2021·浙江浙江·八年级期末)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB; ③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A.①② B.②③ C.①②③ D.①③
【答案】C
解:∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB=180°﹣∠CBA﹣∠CAB=180°﹣(180°﹣∠C)=90°+∠C,①正确;
∵∠C=60°,
∴∠BAC+∠ABC=120°,
∵AE,BF分别是∠BAC与ABC的平分线,
∴∠OAB+∠OBA=(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
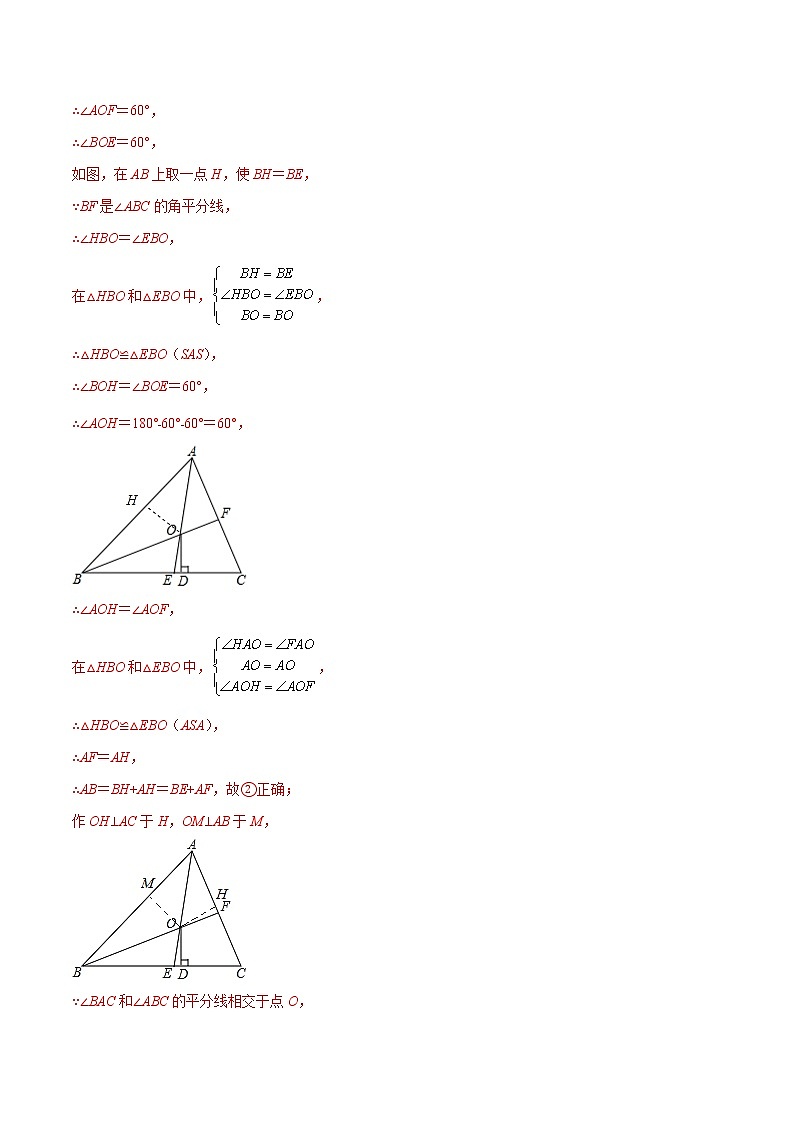
∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,
∴∠HBO=∠EBO,
在△HBO和△EBO中,,
∴△HBO≌△EBO(SAS),
∴∠BOH=∠BOE=60°,
∴∠AOH=180°﹣60°﹣60°=60°,
∴∠AOH=∠AOF,
在△HBO和△EBO中,,
∴△HBO≌△EBO(ASA),
∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OH=OM=OD=a,
∵AB+AC+BC=2b
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC)•a=ab,④正确.
故选:C.
【点睛】
本题主要考查了三角形内角和定理,三角形外角的性质,三角形全等的性质和判定,正确作出辅助线证得△HBO≌△EBO,得到∠BOH=∠BOE=60°,是解决问题的关键.
3.(2021·江西大余·八年级期末)如图,在和中,,连接交于点,连接.下列结论:①;②;③平分;④平分.其中正确的个数为( ).
A.4 B.3 C.2 D.1
【答案】B
解:∵,
∴,
即,
在和中,,
∴,
∴,①正确;
∴,
由三角形的外角性质得:
∴°,②正确;
作于,于,如图所示:
则°,
在和中,,
∴,
∴,
∴平分,④正确;
正确的个数有3个;
故选B.
【点睛】
本题是一道几何的综合型题目,难度系数偏上,关键在于利用三角形的全等证明来证明线段相等,角相等.
4.(2021·浙江浙江·八年级期末)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
【答案】A
∵BF∥AC,∴∠C=∠CBF, ∵BC平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,
∴AB=AC,∵AD是△ABC的角平分线,∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,,∴△CDE≌△DBF,∴DE=DF,CE=BF,故①正确;
∵AE=2BF,∴AC=3BF,故④正确.
故选A.
考点:1.全等三角形的判定与性质;2.角平分线的性质;3.全等三角形的判定与性质.
5.(2021·山东南区·八年级期末)如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F; ②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C.其中正确个数是( )
A.4个 B.3个 C.2个 D.1个
【答案】B
解:①∵BD⊥FD,∴∠FGD+∠F=90°,∵FH⊥BE,∴∠BGH+∠DBE=90°,∵∠FGD=∠BGH,∴∠DBE=∠F,①正确;
②∵BE平分∠ABC,∴∠ABE=∠CBE,∠BEF=∠CBE+∠C,∴2∠BEF=∠ABC+2∠C,∠BAF=∠ABC+∠C,∴2∠BEF=∠BAF+∠C,②正确;
③∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∵∠CBD=90°﹣∠C,∴∠DBE=∠BAC﹣∠C﹣∠DBE,由①得,∠DBE=∠F,∴∠F=∠BAC﹣∠C﹣∠DBE,③错误;
④∵∠AEB=∠EBC+∠C,∵∠ABE=∠CBE,∴∠AEB=∠ABE+∠C,∵BD⊥FC,FH⊥BE,∴∠FGD=∠FEB,∴∠BGH=∠ABE+∠C,④正确.
故选:B.
【点睛】
本题考查的是三角形内角和定理,正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键.
6.(2021·陕西师大附中八年级期末)如图,在△ABC中,AC=2,∠ABC=45°,∠BAC=15°,将△ABC沿直线AC翻折至△ABC所在的平面内,得△ADC.过点A作AE,使∠EAD=∠DAC,与CD的延长线交于点E,则线段ED的长为( )
A.2﹣ B.2﹣2 C.2﹣ D.3﹣
【答案】D
解:如图,延长BC交AE于H,
∵∠ABC=45°,∠BAC=15°,
∴∠ACB=120°,
∵将△ACB沿直线AC翻折,
∴∠DAC=∠BAC=15°,∠ADC=∠ABC=45°,∠ACB=∠ACD=120°,CB=CD,
∵∠DAE=∠DAC,
∴∠DAE=∠DAC=15°,
∴∠CAE=30°,
∵∠ADC=∠DAE+∠AED,
∴∠AED=45°-15°=30°,
∴∠AED=∠EAC,
∴AC=EC=2,
∵∠ABC=45°,∠BAH=45°,
∴∠BHA=90°,BH=AH,
在Rt△ACH中,∠CAH=30°,AC=2,
∴CH=,BH=AH=,
∴CB=CD=BH-CH=,
∴ED=EC-CD=,
故选:D.
【点睛】
本题考查了轴对称的性质,等腰直角三角形的性质和直角三角形的性质等知识,灵活运用这些性质进行推理是本题的关键.
7.(2021·广东光明·八年级期末)如图,BH是△ABC的角平分线,BA=BC=10,AC=12,P,D分别是BH和AB上的任意一点,连接PA,PC,PD,CD.给出下列结论:①PA=PC;②PA+PD≥CD;③PA+PD的最小值是;④若PA平分∠BAC,则△APH的面积为12.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
【答案】A
解:∵BA=BC,BH是角平分线,
∴BH⊥AC,AH=CH,
∴PA=PC,故①正确,
∴PA+PD=PD+PC≥CD,故②正确,
根据垂线段最短可知,当CD⊥AB时,即C,P,D共线时,PA+PD的值最小,最小值为CD,
在Rt△ABH中,AB=10,AH=6,BH===8,
∵•AB•CD=•AC•BH,
∴CD==,
∴PA+PD的最小值为,故③正确,
如图,过点P作PT⊥AB于T.
在△PAT和△PAH中,
,
∴△PAT≌△PAH(AAS),
∴AT=AH=6,PT=PH,
设PT=PH=x,
在Rt△PTB中,则有(8﹣x)2=x2+42,
∴x=3,
∴S△APH=×AH×PH=×3×6=9,故④错误,
故选A.
【点睛】
本题主要考查了轴对称最短问题、等腰三角形的性质、勾股定理、线段的垂直平分线的性质等知识点,证明BH垂直平分线段AC以及灵活参数构建方程解决问题成为解答本题的关键.
8.(2021·四川青神·八年级期末)已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C
试题分析:①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∵在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS).∴BD=CE.本结论正确.
②∵△BAD≌△CAE,∴∠ABD=∠ACE.
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°.∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°.
∴BD⊥CE.本结论正确.
③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°.∴∠ABD+∠DBC=45°.
∵∠ABD=∠ACE,∴∠ACE+∠DBC=45°.本结论正确.
④∵BD⊥CE,∴在Rt△BDE中,利用勾股定理得:BE2=BD2+DE2.
∵△ADE为等腰直角三角形,∴DE=AD,即DE2=2AD2.
∴BE2=BD2+DE2=BD2+2AD2.
而BD2≠2AB2,本结论错误.
综上所述,正确的个数为3个.故选C.
9.(2021·广东高明·八年级期末)一次函数与的图象如图所示,下列说法:①对于函数来说,y随x的增大而增大.②函数不经过第二象限.③不等式的解集是. ④,其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
【答案】B
解:由图象可得:对于函数来说,从左到右,图象上升,y随x的增大而增大,故①正确;
由图象可知,a>0,d>0,所以函数的图象经过第一,二,三象限,即不经过第四象限,故②错误,
由图象可得当时,一次函数图象在的图象上方,
不等式的解集是,
移项可得,,解集是,故③正确;
∵一次函数与的图象的交点的横坐标为4,
∴
∴,
∴,故④正确,
故选:B.
【点睛】
本题考查了一次函数图象的性质和一次函数与不等式的关系,解题关键是树立数形结合思想,理解图象反应的信息,综合一次函数、不等式、方程解决问题.
10.(2021·广东龙岗·八年级期末)如图,已知直线AB:y=x+分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE,当BD+BE的值最小时,则H点的坐标为( )
A.(0,4) B.(0,5) C.(0,) D.(0,)
【答案】A
解:由题意A(0,),B(-3,0),C(3,0),
∴AB=AC=8,
作EF⊥BC于F,设AD=EC=x.
∵EF∥AO,
∴,
∴EF=,CF=,
∵OH∥EF,
∴,
∴OH=,
∴BD+BE=+=+,
要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到K(,3),G(,)的距离之和最小.
设G关于x轴的对称点G′(,),直线G′K的解析式为y=kx+b,
则有,
解得k=,b=,
∴直线G′K的解析式为y=x,
当y=0时,x=,
∴当x=时,MG+MK的值最小,此时OH===4,
∴当BD+BE的值最小时,则H点的坐标为(0,4),
故选A.
【点睛】
本题考查一次函数图象上的点的特征、轴对称最短问题、勾股定理、平行线分线段成比例定理等知识,解题的关键是学会用转化的思想思考问题,属于中考选择题中的压轴题.
11.(2021·四川内江·八年级期末)如图1,已知 AB=AC,D为∠BAC 的平分线上一点,连接 BD、 CD;如图2,已知 AB= AC,D、E为∠BAC的平分线上两点,连接 BD、CD、BE、CE;如图3,已知 AB=AC,D、E、F为∠BAC的平分线上三点,连接BD、CD、BE、CE、 BF、CF;…,依次规律,第 n个图形中全等三角形的对数是( )
A.n B.2n-1 C. D.3(n+1)
【答案】C
解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD.
∴图1中有1对三角形全等;
同理图2中,△ABE≌△ACE,
∴BE=EC,
∵△ABD≌△ACD.
∴BD=CD,
又DE=DE,
∴△BDE≌△CDE,
∴图2中有3对三角形全等;
同理:图3中有6对三角形全等;
由此发现:第n个图形中全等三角形的对数是.
故选:C.
【点睛】
此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.
12.(2021·河南·嵩县教育局基础教育教学研究室八年级期末)如图,已知,,,,和交于点,则下列结论::①;②;③平分;④.其中正确的有( )
A.①② B.①②③ C.①②③④ D.①②④
【答案】C
解:∵,,,
,
即,
在与中,
,
,
,,故①正确,
,,,
,
,故②正确,
连接,过分别作与,于,如图1,
,
,
,而,
,
平分,所以③正确,
在上截取,
,
是等边三角形,
,,
,
,
,
,
;
故④正确;
故选:.
【点睛】
本题考查了等边三角形的性质、全等三角形的判定和性质、角平分线的判定定理等知识,利用全等三角形面积相等证明高相等是解决问题的关键.
13.(2021·湖北·广水市教学研究室八年级期末)如图,,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于点F,且垂足为E,下面的结论:①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的是( )
A.①②③ B.①③⑤ C.②③④ D.②④⑤
【答案】B
解:,,
,
,,
,
,
,
,
,
,①正确;
,
②错误;
,
,
,
,
,
,
AE平分∠BAC,
,
BF⊥AE,
,
,
,
,
.
③正确;
,,
,
④错误;
由,
,
平分,,
,,
,,
,
⑤正确;
故答案为:①③⑤.
故选:B.
【点睛】
本题主要考查对三角形的内角和定理,全等三角形的性质和判定,角平分线的定义,垂线,等腰三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行证明是证此题的关键.
14.(2021·四川乐山·八年级期末)如图,在中,,于,平分,且于,与相交于点,是边的中点,与交于点.某数学兴趣小组分析图形后得出以下结论:①;②;③;④.上述结论一定正确的是( )
A.①③ B.②④ C.①②④ D.①②③④
【答案】C
解:
,
∵是边的中点,
故②正确;
,,
在和中,
,
,故①正确;
平分,且,
在和中,
,
,故④正确;
如图,过点G作于K,
平分,且,
,
∵在中,>,
<,故③错误.
故选:C.
【点睛】
本题考查了等腰直角三角形的判定与性质,角平分线的性质,全等三角形的判定与性质,仔细分析图形并熟练掌握各知识点是解题的关键.
15.(2021·重庆巴南·八年级期末)如图,在中,,点D在边AC上,,且与关于直线BD对称.现有如下4个结论:①,②,③,④,其中正确的结论有( )
A.4 B.3个 C.2个 D.1个
【答案】A
解:∵∠ABC=90°,
∴∠A+∠C=90°,∠ABD+∠DBC=90°,
∵BD=CD,
∴∠C=∠DBC,
∴∠ADB=∠DBC+∠C=2∠C,∠A=∠ABD,
∴AD=BD,即AC=AD+CD=2BD,①正确;
根据折叠的性质可知∠DBE=∠ABD,∠ADB=∠BDE,
∴∠DBE=∠ABD=∠A,∠ADB=∠BDE=2∠C,
∴∠CBE=2∠A-90°,∠CDE=180°-4∠C,
∴
,②正确;
∵,
∴,③正确;
∴,④正确;
综上所述,正确的有4个,
故选:A.
【点睛】
本题考查三角形外角的性质,等边对等角,折叠问题,直角三角形两锐角互余等.解决此题的关键是熟练掌握定理,分别正确表示相应角.
相关试卷
这是一份【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练10 压轴大题(15题),文件包含期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练10压轴大题15题解析版docx、期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练10压轴大题15题原卷版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
这是一份【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练06 填空题-压轴(15题),文件包含期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练06填空题-压轴15题解析版docx、期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练06填空题-压轴15题原卷版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
这是一份【期末考前必练】2022-2023学年苏科版数学八年级上册期末考点必刷题:专练02 选择题-提升(20题),文件包含期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练02选择题-提升20题解析版docx、期末考前必练2022-2023学年苏科版数学八年级上册期末考点必刷题专练02选择题-提升20题原卷版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。









