




【期末仿真检测】苏科版数学 九年级上学期-期末测试卷02(提高卷)(苏州专用)
展开2022-2023学年九年级上学期期末测试卷02
数学
班级___________ 姓名___________ 分数____________
(考试时间:120分钟 试卷满分:130分)
【考试范围:苏教九年级上册全部】
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若关于x的方程有一个根是1,则a等于( )
A. B. C.3 D.1
【答案】B
【解析】把代入得:,
解得:.故选:B.
2.已知关于x的一元二次方程,则下列关于该方程根的判断,正确的为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.实数根的个数与实数m的取值有关
【答案】B
【解析】解:根据题意得△=m2-4×1×(-1)=m2+4,
∵m2≥0,
∴m2+4>0,即△>0,
∴方程有两个不相等的实数根.
故选:B.
3.有一组数据:1,2,3,3,4.这组数据的众数是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】解:∵3出现了2次,出现的次数最多,
∴这组数据的众数为3;故选:C.
4.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为188cm的队员换下场上身高为194cm的队员,与换人前相比,场上队员的身高()
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
【答案】A
【解析】解:原数据的平均数为,
则原数据的方差为×[(180-188)2+(184-188)2+(188-188)2+(190-188)2+(192-188)2+(194-188)2]= ,
新数据的平均数为,
则新数据的方差为×[(180-187)2+(184-187)2+(188-187)2+(190-187)2+(188-187)2+(192-187)2]= ,
所以平均数变小,方差变小,故选:A.
5.如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么指针同时落在偶数的概率是( )
A. B. C. D.
【答案】B
【解析】解:列表得,
1
2
4
5
6
1
1,1
1,2
1,4
1,5
1,6
2
2,1,
2,2,
2,4
2,5
2,6
3
3,1
3,2
3,4
3,5
3,6
4
4,1
4,2
4,4
4,5
4,6
5
5,1
5,2
5,4
5,5
5,6
共有5×5=25种可能,指针同时落在偶数的结果有(2,2)、(2,4)、(2,6)、(4,2)、(4,4)、(4,6)共6种,
所以指针同时落在偶数的概率是.故选:B.
6.下列说法中,不正确的是( )
A.同圆中,直径是最长的弦 B.同圆中,所有的半径都相等
C.圆既是轴对称图形又是中心对称图形 D.长度相等的弧是等弧
【答案】D
【解析】解:A、同圆中,直径是最长的弦,说法正确,不符合题意;B、同圆中,所有的半径都相等,说法正确,不符合题意;C、圆既是轴对称图形又是中心对称图形,说法正确,不符合题意;D、长度相等的弧是等弧,说法错误,符合题意;故选:D.
7.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】解:①优弧不一定比劣弧长,在同圆或等圆中,优弧比劣弧长,故①错误,符合题意;②不在用一直线上的三点可以确定一个圆,故②错误,符合题意;③长度相等的弧不一定是等弧,故③错误,符合题意;④经过圆内的一个定点可以作无数条弦,正确,故④不符合题意,故不正确的有①②③,故选:C.
8.将一个底面半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )
A. B. C. D.
【答案】D
【解析】解:将一个半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,
圆锥侧面积公式为:,
扇形面积为,
解得:,
侧面展开图的圆心角是144度.故选:.
9.如图,把圆分成六等分,经过各分点作圆的切线,以相邻切线的交点为顶点的图形是这个圆的外切正六边形,⊙O的半径是R,它的外切正六边形的边长为( )
A. B. C. D.
【答案】A
【解析】如图,∵∠AOB=,AO=BO
∴△AOB是等边三角形
作CO⊥AB
∴CO=R
∠AOC=∠AOB=30°
∴AC=AB=AO
∵AO2=AC2+CO2
∴AO2=(AO)2+R2
∴AO=,
故选A.
10.规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”现有下列结论:①方程x2+2x﹣8=0是倍根方程;②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;③若(x﹣3)(mx﹣n)=0是倍根方程,则n=6m或3n=2m;④若点(m,n)在反比例函数y=的图象上,则关于x的方程mx2﹣3x+n=0是倍根方程.上述结论中正确的有( )
A.② B.①③ C.②③④ D.②④
【答案】D
【解析】解:①x2+2x﹣8=(x+4)(x-2)=0,∴x1=-4,x2=2,x1=-2x2,不是倍根方程,错误;
②由题意得:2x12=2,∴x1=±1,∴x1=1,x2=2,x1=-1,x2=-2,则a=x1+x2=±3,正确;
③ ∵x1=3,x2=,当x1=2x2时,3m=2n,当x2=2x1时,n=6m,错误;
④由题意得:n=,∴mx2-3x+=0,∴x1+x2=,x1x2=, 整理得:2x12-5x1x2+2x22=0,∴(x1-2x2)(2x1-x2)=0,∴x1=2x2, 或x2=2x1,正确;综上,正确的是 ②④.故答案为D.
二、填空题:(本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上)
11.某鞋厂调查了商场一个月内不同尺码运动鞋的销量,在平均数、中位数、众数这三个统计量中,该鞋厂最关注的是________.
【答案】众数
【解析】解:由于众数是数据中出现最多的数,故鞋厂最感兴趣的销售量最多的尺码即这组数据的众数.
故答案:众数.
12.某家庭电话,打进的电话响第一声时被接的概率为0.1,响第二声被接的概率为0.2,响第三声或第四声被接的概率都是0.25,则电话在响第五声之前被接的概率为___________.
【答案】0.8
【解析】打进的电话响第一声时被接的概率为0.1,响第二声被接的概率为0.2,响第三声或第四声被接的概率都是0.25,
电话在响第五声之前被接的概率为.故答案为:0.8.
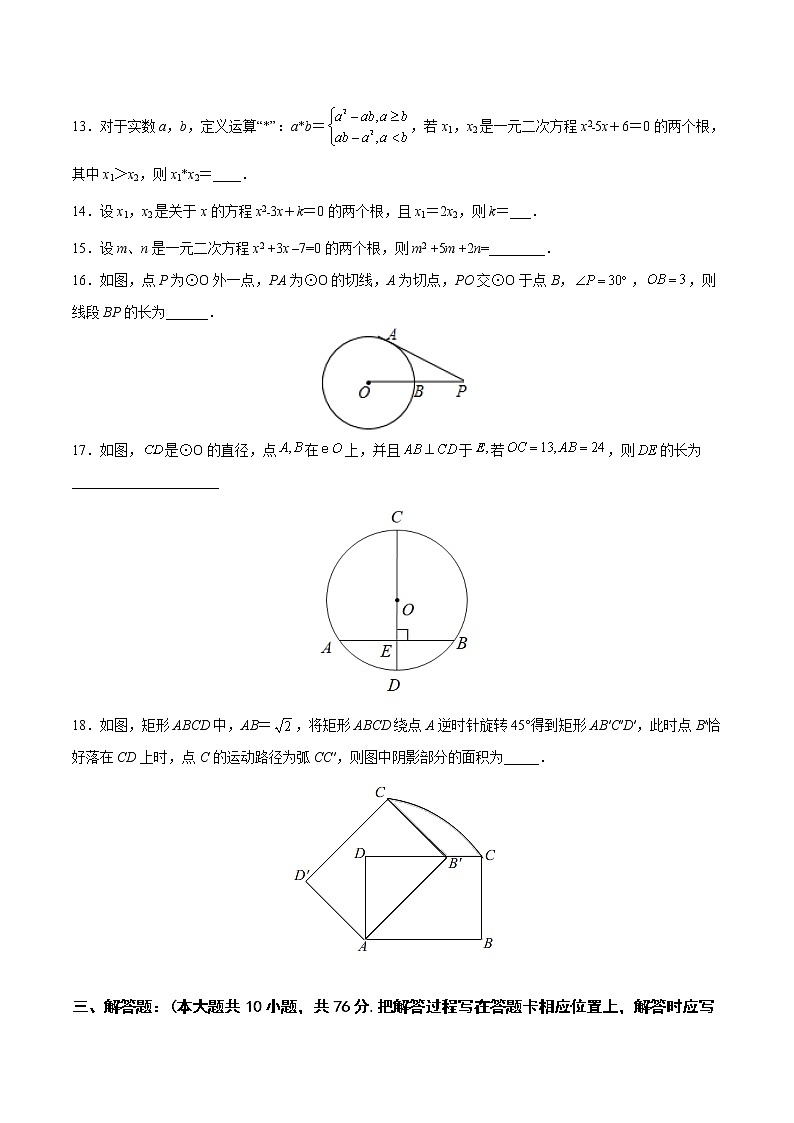
13.对于实数a,b,定义运算“*”:a*b=,若x1,x2是一元二次方程x2﹣5x+6=0的两个根,其中x1>x2,则x1*x2=____.
【答案】3或2或3
【解析】解:解方程x2﹣5x+6=0得x=3或x=2,
当x1=3,x2=2时,x1*x2=32﹣3×2=3;
当x1=2,x2=3时,x1*x2=2×3﹣22=2.
故答案为:3或2.
14.设x1,x2是关于x的方程x2﹣3x+k=0的两个根,且x1=2x2,则k=___.
【答案】2
【解析】解:∵x1,x2是关于x的方程x2﹣3x+k=0的两个根,
∴,,
又∵x1=2x2,
∴,解得:,,
∴.故答案为:2.
15.设m、n是一元二次方程x2 +3x –7=0的两个根,则m2 +5m +2n=________.
【答案】1
【解析】解:、是一元二次方程的两个根,
,,
,
.
故答案为:1.
16.如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,,,则线段BP的长为______.
【答案】3
【解析】如图所示:连接OA,
∵PA为⊙O的切线,
∴,
∵,,
∴,则,
故.
故答案为:3.
17.如图,是⊙O的直径,点在上,并且于若,则的长为_____________________
【答案】
【解析】连接,如图,
是⊙O的直径,,,
在中,
故答案为:
18.如图,矩形ABCD中,AB=,将矩形ABCD绕点A逆时针旋转45°得到矩形AB′C′D′,此时点B′恰好落在CD上时,点C的运动路径为弧CC′,则图中阴影部分的面积为_____.
【答案】
【解析】解:如图连接AC,AC′,过B′作B′E⊥AB于E,
∵将矩形ABCD绕点A旋转得到矩形AB′C′D′,
∴∠B′AE=∠B′AD=∠C′AC=,AB′=AB=,AC′=AC,
∴△B′AD是等腰直角三角形,
∴四边形B′EAD是正方形,且AD=DB′=1,
∴B′E=AD=AE=DB′=1,
AC′=AC=,
∴B′C=BE=,
∴图中阴影部分的面积=S扇形C′AC-S△AB'C′-S△AB′C
故答案为:.
三、解答题:(本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明作图时用2B铅笔或黑色墨水签字笔.)
19.(5分)19.计算:
【答案】
【解析】解:
20.(5分)解方程:x2+2x=x+2.
【答案】
【解析】解:x2+2x=x+2
移项得:
或
解得:
21.(6分)先化简,再求值:,其中是满足不等式组的整数解之一.
【答案】当时,原式;当时,原式
【解析】解:
解不等式组,解不等式①得:,解不等式②得:,
故,
∵为整数,
∴可为0,1,2.
∵且,
∴或2.
∴当时,原式;当时,原式.
22.(6分)某校举办了国学知识竞赛,满分分,学生得分均为整数.在初赛中,甲乙两组学生成绩如下(单位:分)
甲组:,,,,,,,,,.
乙组:,,,,,,,,,.
组别
平均数
中位数
方差
甲组
乙组
(1)以上成绩统计分析表中________,________;
(2)小明同学说:“这次竞赛我得了分,在我们小组中属中游略偏上!”观察上面表格判断,小明可能是________组的学生;
(3)如果你是该校国学竞赛的辅导员,你会选择哪一组同学代表学校参加复赛?并说明理由.
【答案】(1)60,68;(2)甲;(3)选乙组同学代表学校参加复赛,理由见解析
【解析】(1)甲组的中位数(分),
乙组的平均数是:(分),
故答案为:60,68;
(2)根据中位数判断,甲组中位数60分,乙组中位数70分,所以小明是在甲组;
(3)乙组的方差是: ,
∵乙组的方差小于甲组,
∴选乙组同学代表学校参加复赛.
23.(8分)“双十一”购物日中不乏冲动消费者,某数学兴趣小组对消费行为进行调查.按购物数量x(件)分为以下4类:A(x≤3),B(x=4),C(x=5),D(x≥6),根据调查结果制作了如下两图统计图(不完整),已知购买4件商品的消费者中,理性购物人数所占比例为80%,根据图中信息回答下列问题:
(1)本次调查的总人数为 人;
(2)补全条形统计图;
(3)小张在“双十一”共购进7件商品,其中4件服装购自“天猫商城”,3件电子产品购自“京东商城”,由于冲动消费,小张决定从服装和电子产品中各随机选择1件进行退货,已知“天猫商城”购买的4件服装中仅1件支持退货,“京东商城”购买的电子产品中仅2件支持退货.请用列表或树状图的方法,求小张选出的2件商品均能退货的概率.
【答案】(1)60人;(2)见解析;(3).
【解析】解:(1)理性购物的总人数为12÷30%=40(人),
则B类理性购物人数为40×40%=16,
∴B类购物人数为16÷80%=20(人),
本次调查的总人数为15+20+15+10=60(人),
故答案为:60;
(2)补全条形统计图为:
(3)用1、2、3、4表示购自“天猫商城”的4件服装,且4为支持退货的服装;3件电子产品用5、6、7表示,且6、7为支持退货的电子产品,
画树状图为:
共有12种等可能的结果,其中小张选出的2件商品均能退货的结果有2种,
∴小张选出的2件商品均能退货的概率=.
24.(8分)如图,AB为⊙O的直径,PQ切⊙O于E,于C.交⊙O于D.
(1)求证:AE平分;
(2)若,求⊙O的半径.
【答案】(1)见解析;(2)
【解析】(1)证明:连接OE,
∴,
∴,
∵PQ切⊙O于E,
∴,
∵,
∴,
∴,
∴,
∴AE平分.
(2)解:过点O作于M,
∴,
又∵,
∴四边形OECM为矩形,
∴,
在中,
,
即⊙O的半径为
25.(8分)某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件,设每件衣服降价x元.
(1)现在每天卖出 件,每件盈利 元(用含x的代数式表示);
(2)求当x为何值时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠;
(3)要想平均每天盈利2000元,可能吗?请说明理由.
【答案】(1)(20+2x),(40﹣x);(2)20;(3)不可能,见解析
【解析】解:(1)由题意得:每天卖出衣服的数量为:(20+2x)件,
每件的盈利为:(90﹣x)﹣50=(40﹣x)元,
故答案为:(20+2x),(40﹣x);
(2)由题意得:
(90﹣x﹣50)(20+2x)=1200,
解得:x1=20,x2=10,
为使顾客得到较多的实惠,应取x=20;
(3)不可能,理由如下:
依题意得:
(90﹣x﹣50)(20+2x)=2000,
整理得:x2﹣30x+600=0,
Δ=(﹣30)2﹣4×600=900﹣2400=﹣1500<0,
则原方程无实数解.
则不可能每天盈利2000元.
26.(10分)如图,在平面直角坐标系中,直线y=﹣x+2与y轴,x轴分别交于点A、B,动点P在线段AB上移动(点P不与点A、点B重合),以点P为顶点作∠OPQ=45°交x轴于点Q.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求证:∠AOP=∠BPQ;
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由;
(4)若点O到直线PQ的距离是 ,请直接写出线段AP的长.
【答案】(1)A(0,2),B(2,0);(2)见解析;(3)存在,点P的坐标为(1,1)或;(4) 或
【解析】解:(1)直线y=-x+2与x轴,y轴分别交于B、A两点,
令x=0,则y=0+2=2,
∴A(0,2),
令y=0,则0=-x+2,解得:x=2,
∴B(2,0);
(2)证明:过P点作PE⊥OA交OA于点E,
∵A (0,2), B (2,0),
∴ OA=OB=2,
∴ ∠OAB= ∠OBA= 45°,
∵PE⊥OA,
∴∠APE=45°,
∵∠OPQ=45°,
∴∠OPE+∠BPQ=90°,
∵∠OPE+∠AOP=90°,
∴∠AOP=∠BPQ;
(3)△OPQ可以是等腰三角形,理由如下:
如图,过点P作PE⊥OA于点E,
若OP=OQ,则∠OPQ=∠OQP=45°,
∴∠POQ=90°,
∴点P与点A重合,
∵点P不与点A、点B重合,
∴此种情况不成立;
若PQ=OQ,则∠OPQ=∠QOP=45°,
∴PQ⊥QO,
可设P(x,x)代入y=-x+2,解得:x=1,
∴点P坐标为(1,1);
若PO=PQ,过P点PM⊥OA交OB于点M,
由(2)知:∠AOP=∠BPQ,
又∵∠3=∠4=45°,
∴△AOP≌△BPQ(AAS),
∴PB=OA=2,
∵∠OBA=45°,
∴△PMB以是等腰直角三角形,PB=2,
∵ ,
∴ ,
∴点 ,
综上所述,点P的坐标为(1,1)或;
(4)如图,过点O作ON⊥PQ,交PQ于点N,过点P作PF⊥OA于点F,则 ,AM=MP,
∵∠OPQ=45°,
∴△PON是等腰直角三角形,
∴ON=PN,
∵ ,
∴ ,
设 ,
∴ ,
在中, ,
即 ,
解得: ,
∴ 或.
27.(10分)(问题情境)
如图1,在△ABC中,,AD⊥BC于点D,,,求AD的长.
(问题解决)
小明同学是这样分析的:将△ABD沿着AB翻折得到△ABE,将△ACD沿着AC翻折得到△ACF,延长EB、FE相交于点G,请按着小明的思路解答下列问题:
(1)由上可得四边形AEGF是 (填矩形、菱形、正方形中的一个);
(2)在Rt△GBC中运用勾股定理,求出AD的长.
(方法提炼)通过问题解决,小明发现翻折是解决问题的有效办法之一,它可以将问题中的相关信息有效地集中、关联与重组.请根据自己的理解,解答下列问题:
(3)如图2,在四边形ABCD中,,,,,求AC的最大值.
(4)如图3,在四边形ABCD中,,AD=2,M是AB上一点,且,,,直接写出CD的最大值为 .
【答案】(1)正方形;(2)12;(3);(4)
【解析】解:(1)四边形AEGF是正方形,理由如下:
由折叠得:,.
,,
又∵,
.
又,
,.
四边形是矩形,
∵,,
∴,,
.
矩形是正方形,
故答案为:正方形;
(2)设,则.
,,
,,
,,
在中,,
.
化简得,,
解得:,(舍去)
∴;
(3)如图①,将沿着AB翻折得到,将沿着AD翻折得到,连接EF,
∴BE=BC=6,DF=CD=8,且AE=AF=AC,,,
又∵,
.
∴,
∵,,,
∴,
∵当BE、BD、DF三条线段共线时,EF最大,
∴EF的最大值为6+8+10=24,
∴AC的最大值为;
(4)如图②,将沿着DM翻折得到,将沿着CM翻折得到,连接EF,
由翻折可得:DE=AD=2,EM=AM=3,MF=BM=4,CF=BC=,,,
∵,
∴,
∴,
∴,
∵EM=3,MF=4,
∴,
∵CD≤DE+EF+FC=,当点D、E、F、C在同一直线上时取得最大值,
∴CD的最大值为,
故答案为:.
28.(10分)问题提出
如图1,AB、AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,
求证:CD=BA+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
如图2,延长CA至E,使AE=AB,连接MA、MB、MC、ME、BC.
∵M是的中点
∴∴∠MCB=∠MAC(请你在下面的空白处完成小敏的证明过程.)
推广运用
如图3,等边△ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是 .
拓展研究
如图4,若将“问题提出”中“M是的中点”改成“M是的中点”,其余条件不变,“CD=BA+AD”这一结论还成立吗?若成立,请说明理由;若不成立,写出CD、BA、AD三者之间存在的关系,并说明理由.
【答案】问题提出:见解析;推广运用:1+;拓展研究:不成立,CD、BA、AD三者之间的关系:AD=BA+CD,理由见解析
【解析】问题提出:证明:如图2,延长CA至E,使AE=AB,连接MA、MB、MC、ME、BC,
∵M是的中点,
∴MB=MC,∠MBC=∠MCB,
∵∠MAB=180°-∠MCB,∠EAM=180°-∠CAM=180°-∠MBC,
∴∠EAM=∠BAM,
在△EAM和△BAM中,
,
∴△EAM≌△BAM(SAS),
∴ME=MB=MC,
又∵MD⊥AC,
∴ED=CD,
∴DC=AD+AE=BA+AD;
推广运用:解:如图3,截取BF=CD,连接AF,AD,CD,
由题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中,
∴△ABF≌ACD(SAS),
∴AF=AD,
∵AE⊥BD,
∴FE=DE,则CD+DE=BE,
∵∠ABD=45°,
∴BE= ,
则△BDC的周长=BC+BD+CD=BC+2BE=1+,
故答案为:1+;
拓展研究:不成立,CD、BA、AD三者之间的关系:AD=BA+CD,
证明:延长MD交圆O于点E,如图④,连接EA,EF,ED,EB交AC于N,
∵M是的中点,
∴∠BEM=∠CEM,
在△EDN和△EDC中,
,
∴△EDN≌△EDC ,
∴CD=ND,∠ECD=∠END,
∵∠ECD=∠ABE,∠ENC=∠ANB,
∴∠ANB=∠ABE,
∴AN=AB,
∴AD=AN+ND=BA+CD.
【期末仿真检测】苏科版数学 七年级上学期-期末测试卷03(提高卷)(苏州专用): 这是一份【期末仿真检测】苏科版数学 七年级上学期-期末测试卷03(提高卷)(苏州专用),文件包含期末仿真检测苏科版数学七年级上学期-期末测试卷03提高卷苏州专用解析版doc、期末仿真检测苏科版数学七年级上学期-期末测试卷03提高卷苏州专用原卷版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
【期末仿真检测】苏科版数学 七年级上学期-期末测试卷02(提高卷)(苏州专用): 这是一份【期末仿真检测】苏科版数学 七年级上学期-期末测试卷02(提高卷)(苏州专用),文件包含期末仿真检测苏科版数学七年级上学期-期末测试卷02提高卷苏州专用解析版doc、期末仿真检测苏科版数学七年级上学期-期末测试卷02提高卷苏州专用原卷版doc等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
【期末仿真检测】苏科版数学 七年级上学期-期末测试卷02(提高卷)(南京专用): 这是一份【期末仿真检测】苏科版数学 七年级上学期-期末测试卷02(提高卷)(南京专用),文件包含期末仿真检测苏科版数学七年级上学期-期末测试卷02提高卷南京专用解析版doc、期末仿真检测苏科版数学七年级上学期-期末测试卷02提高卷南京专用原卷版doc等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












