【期末总复习】人教版数学 九年级上学期-期末高分押题模拟试卷（三）

九年级数学期末高分押题模拟试卷（三）

一、单选题

1．下列方程是一元二次方程的是（    ）

A． B．

C． D．

2．新冠病毒主要是经呼吸道飞沫传播的，在无防护下传播速度很快，已知有1个人患了新冠，经过两轮传染后共有625个人患了新冠，每轮传染中平均一个人传染m人，则m的值为（　　　）

A．20 B．22 C．24 D．25

3．若点A(-3，a)与点B(b，4)关于原点对称，则a的值是(     )

A．4 B．3 C．-4 D．-3

4．在两个不透明的口袋中分别装有两把不同的钥匙和三把锁，其中两把钥匙分别能打开两把锁，且不能打开第三把锁，随机取出一把钥匙和一把锁，能打开的概率是（    ）

A． B． C． D．

5．给出下列4个命题，其中是真命题的是（      ）

A．经过三个点一定可以作圆． B．等弧所对的圆周角相等．

C．相等的圆周角所对的弧相等． D．圆的对称轴是直径．

6．如图，是的外接圆，交于点，连结．若，，则的度数为（     ）

A． B． C． D．

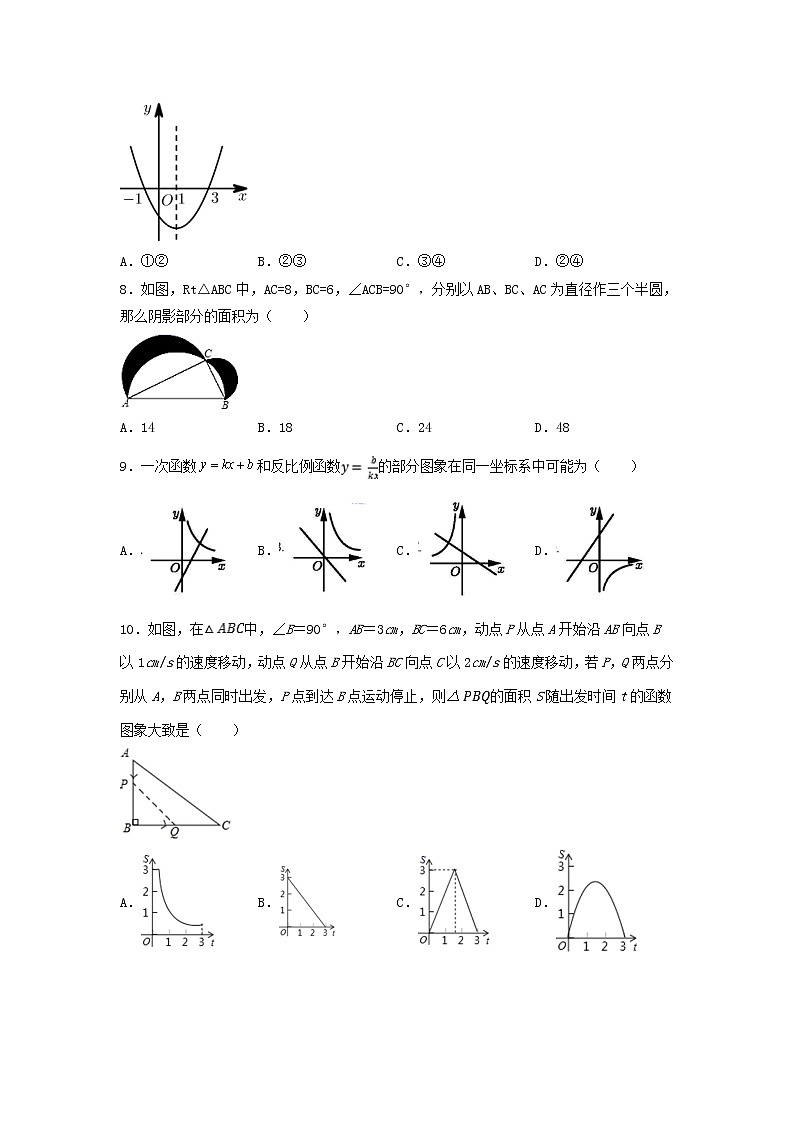
7．二次函数的图象如图所示，则下列说法：①；②；③；④当时，y随x的增大而减小，其中正确的结论是（    ）

A．①② B．②③ C．③④ D．②④

8．如图，Rt△ABC中，AC=8，BC=6，∠ACB=90°，分别以AB、BC、AC为直径作三个半圆，那么阴影部分的面积为（　　）

A．14 B．18 C．24 D．48

9．一次函数和反比例函数的部分图象在同一坐标系中可能为（    ）

A． B． C． D．

10．如图，在中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动，若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则的面积S随出发时间t的函数图象大致是（　　）

A． B． C． D．

二、填空题

11．已知y1=x2-9，y2=3-x，当x=______________时，y1=y2．

12．如图，抛物线y＝ax2+bx与直线y＝kx相交于O，A（3，2）两点，则不等式ax2+bx﹣kx＜0的解集是____________．

13．已知圆锥的轴截面是边长为6的等边三角形，则这个圆锥侧面展开图的圆心角为______度．

14．在永辉超市的一次抽奖活动中，在一个不透明的纸质箱中，规定抽中红球为一等奖．装有黑球25个，白球15个，红球6个，这些球除颜色不同外没有任何区别，现从中任意摸出个球，要使中一等奖的概率为，需要往这个口袋再放人同种红球__________个．

15．如图，圆锥的底面圆直径为，母线长为，若小虫从点开始绕着圆锥表面爬行一圈到的中点，则小虫爬行的最短距离为________．

16．如图，是的直径，交的中点于，于，连接，则下列结论正确的有______（填序号）

①；②；③；④是的切线．

17．已知点A（2，3）在反比例函数的图象上，当x>-2且x≠0时，则y的取值范围是_________．

三、解答题（一）

18．用适当的方法解一元二次方程：

（1）（2x﹣1）2﹣3＝0；

（2）x（x﹣4）＝1．

19．如图，△ABC的顶点坐标分别为A（0，1），B（3，3），C（1，3）．

（1）画出△ABC关于点O的中心对称图形△A1B1C1．

（2）①画出△ABC绕原点O逆时针旋转90°的△A2B2C2；

②直接写出点B2的坐标为　   　．

20．请你利用直尺和圆规把弧四等分．

四、解答题（二）

21．某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如表：

已知y是x的一次函数．

（1）求日销售量y（件）与每件产品的销售价x（元）之间的函数表达式；

（2）当每件产品的销售价定为35元时，此时每日的销售利润是多少元？

（3）销售价定为多少时，每日的销售利润最大？最大利润是多少？

22．钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，尽量呆在家，勤洗手，多运动，多看书，少熬夜．”重庆实验外国语学校为鼓励学生抗疫期间在家阅读，组织八年级全体同学参加了疫期居家海量读书活动，随机抽查了部分同学读书本数的情况统计如图所示．

（1）本次共抽查学生______人，并将条形统计图补充完整；

（2）读书本数的众数是______本，中位数是_______本．

（3）在八年级2000名学生中，读书15本及以上（含15本）的学生估计有多少人？

（4）在八年级六班共有50名学生，其中读书达到25本的有两位男生和两位女生，老师要从这四位同学中随机邀请两位同学分享读书心得，试通过画树状图或列表的方法求恰好是两位男生分享心得的概率．

23．如图所示，一次函数的图象与反比例函数的图象交于．

（1）求反比例函数和一次函数的解析式；

（2）在x轴上存在一点C，使为等腰三角形，求此时点C的坐标；

（3）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．

五、解答题（三）

24．如图示，AB是⊙O的直径，点F是半圆上的一动点（F不与A，B重合），弦AD平分∠BAF，过点D作DE⊥AF交射线AF于点AF．

（1）求证：DE与⊙O相切：

（2）若AE＝8，AB＝10，求DE长；

（3）若AB＝10，AF长记为x，EF长记为y，求y与x之间的函数关系式，并求出AF•EF的最大值．

25．已知抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，﹣3），顶点D的坐标为（1，﹣4）．

（1）求抛物线的解析式．

（2）在y轴上找一点E，使得△EAC为等腰三角形，请直接写出点E的坐标．

（3）点P是x轴上的动点，点Q是抛物线上的动点，是否存在点P、Q，使得以点P、Q、B、D为顶点，BD为一边的四边形是平行四边形？若存在，请求出点P、Q坐标；若不存在，请说明理由．

参考答案

1．C

A．，二次项系数不为零，本选项不符合题意；

B．，化简后是一元一次方程，本选项不符合题意；

C．，是一元二次方程，本选项符合题意；

D．，方程含有两个未知数，本选项不符合题意；

故选：C．

2．C

由题意，第一轮会有人被传染，

第二轮会有人被传染，

则，

解得或（不符题意，舍去），

故选：C．

3．C

点A(-3，a)与点B(b，4)关于原点对称，a=-4，

故选择：C．

4．B

画树状图为：

共有6种等可能的结果数，随机取出一把钥匙和一把锁，能打开的结果数为2，

∴随机取出一把钥匙和一把锁，能打开的概率为＝；

故选：B．

5．B

解：A、经过不在同一直线上的三个点一定可以作圆，本选项说法是假命题；

B、等弧所对的圆周角相等，本选项说法是真命题；

C、在同圆或等圆中，相等的圆周角所对的弧相等，本选项说法是假命题；

D、圆的对称轴是直径所在的直线，本选项说法是假命题；

故选：B．

6．B

解：连接OA，OB，

∵，，

∴∠ACB=180°-70°-38°=72°，

∵∠BAC=∠BOC，∠ABC=∠AOC，

∴∠BOC=2∠BAC=2×70°=140°，∠AOC=2∠ABC=2×38°=76°，

∴∠AOB=360°-∠BOC-∠AOC=144°，
∵D为的中点，∴，
∴∠AOD=∠BOD=∠AOB=×144°=72°．

∴ =∠AOD+∠AOC=72°+76°=148°，

故选：B．

7．D

解：①根据图示知，抛物线开口方向向上，抛物线与y轴交与负半轴，

∴a＞0，c＜0，

∵->0，

∴b＜0，

所以abc＞0．故①错误；

②根据图象得对称轴x=1，即-=1，所以b=-2a，即2a+b=0，故②正确；

③当x=3时，y=0，即9a+3b+c=0．故③错误；

④根据图示知，当x＜0时，y随x的增大而减小，故④正确；

故选：D．

8．C

解：Rt△ABC中，AC=8，BC=6，∠ACB=90°，

S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC－直径为AB的半圆的面积

=24．

故答案选：C．

9．C

故选：C．

10．D

设运动时间为，

点P到达点B所需时间为，点Q到达点C所需时间为，

点P、Q同时停止运动，且的取值范围为，

由题意，，

，

，

，

则与之间的函数图象是抛物线在的部分，且开口向下，

观察四个选项可知，只有选项D符合，

故选：D．

11．3或-4

解：根据题意得：

x2-9=3-x

或

∴；

故答案为：3或-4．

12．0＜x＜3

将原不等式变形为ax2+bx＜kx

∵抛物线y＝ax2+bx与直线y＝kx相交于点A(3,2)，点O(0,0)

∴方程ax2+bx=kx的解为：x=0或x=3

根据图像可知：不等式ax2+bx＜kx的解集为：0＜x＜3

故答案为：0＜x＜3．

13．180

设这个圆锥侧面展开图的圆心角为度，

圆锥的轴截面是边长为6的等边三角形，

圆锥的底面直径和母线长均为6，

由圆锥的侧面积公式得：，

又圆锥的侧面展开图是扇形，

，

解得，

即这个圆锥侧面展开图的圆心角为180度，

故答案为：180．

14．4

解：设需要往这个口袋再放入同种红球个．

根据题意得：，

解得：，

故答案为：4．

15．

把圆锥的侧面展开，弧长是2πr=2π，母线AS=4，

侧面展开的圆心角，n=90º即∠ASC=90º，

C为AD的中点SD=2，

线段AC是小虫爬行的最短距离，

在Rt△SAC中，由勾股定理的AC=，

故答案为：．

16．①②③④

解：∵是的直径，

∴∠ADB=90°，

∴AD⊥BC，故①正确；

∵点D是BC的中点，

∴AC=AB，

∴△ABC是等腰三角形，

∴∠B=∠C，∠CAD=∠BAD，

∵DE⊥AC，∠CDA=90°，

∴∠EDA+∠EAD=90°，∠CAD+∠C=90°，

∴，

∴，故②正确；

∵，

∴，故③正确；

连接OD，如图所示：

∵OD=OA，

∴∠ADO=∠DAO，

∴∠ADO=∠EAD，

∴∠ADO+∠EDA=90°，

∴ED是⊙O的切线，故④正确；

∴正确的有①②③④；

故答案为①②③④．

17．

解：把点A（2，3）代入反比例函数可得：

，解得k=6，

∴反比例函数的解析式为，

当x=-2时，y=-3，

∴当时，则有y的取值范围为y<-3，

当时，则有y的取值范围为y>0；

综上所述：或；

故答案为或．

18．

解：（1）∵（2x﹣1）2﹣3＝0，

∴（2x﹣1）2＝3，

则2x﹣1＝±，

∴x1＝，x2＝；

（2）整理，得：x2﹣4x＝1，

则x2﹣4x+4＝1+4，即（x﹣2）2＝5，

∴x﹣2＝±，

解得x1＝2+，x2＝2﹣．

19．

解：（1）如图，△A1B1C1为所作；

（2）①画如图，△A2B2C2为所作；

②点B2的坐标为（﹣3，3）．

故答案为（-3，3）．

20．答案见详解．

以A、B两点为圆心，以大于AB为半径画弧，两弧交于G、H两点，过G、H作直线GH交圆弧与C，

连结AC、BC，

以A、C两点为圆心，以大于AC为半径画弧，两弧交于M、N两点，过M、N作直线MN交圆弧与E，

以B、C两点为圆心，以大于BC为半径画弧，两弧交于P、Q两点，过P、Q作直线PQ交圆弧与D，

则E、C、D三点把圆弧四等分．

21．

（1）设，根据题意可得：

，
解得：，
故日销售量y（件）与每件产品的销售价x（元）之间的函数表达式为：；
（2）当每件产品的销售价定为35元时，

此时每日的销售利润是：（元），
答：此时每日的销售利润是125元；
（3）设总利润为w，根据题意可得：
，
∵，
∴销售价定为25元时，每日的销售利润最大，最大利润是225元．

22．

解：（1）调查总人数为14÷28%=50（人）

故答案为：50；

读10本书的人数为50－9－14－7－4=16（人）

补全条形统计图如下：

（2）根据众数的定义：读书本数的众数是10本，

根据中位数的定义：中位数是（10＋15）÷2= （本）

故答案为：10；；

（3）（人）

答：在八年级2000名学生中，读书15本及以上（含15本）的学生估计有1000人；

（4）画树状图如下：

一共有12种等可能的结果，其中恰好是两位男生分享心得的结果有2种

∴恰好是两位男生分享心得的概率为2÷12=．

23．

解：（1）把A（3，4）代入，

∴m＝12，

∴反比例函数是；

把B（n，-1）代入得n＝−12．

把A（3，4）、B（-12，−1）分别代入y＝kx＋b中：

得，

解得，

∴一次函数的解析式为；

（2）∵A（3，4），△AOC为等腰三角形，OA=，

分三种情况：

①当OA=OC时，OC=5，

此时点C的坐标为，；

②当AO=AC时，∵A（3，4），点C和点O关于过A点且垂直于x轴的直线对称，

此时点C的坐标为；

③当CA=CO时，点C在线段OA的垂直平分线上，

过A作AD⊥x轴，垂足为D，

由题意可得：OD=3，AD=4，AO=5，设OC=x，则AC=x，

在△ACD中，

，

解得：x=，

此时点C的坐标为；

综上：点C的坐标为：，，，；

（3）由图得：

当一次函数图像在反比例函数图像上方时，

-12<x<0或x>3，

即使一次函数的值大于反比例函数的值的x的取值范围是：-12<x<0或x>3.

24．

（1）证明：连接OD，如图1所示：

∵OD＝OA，

∴∠OAD＝∠ODA，

∵AD平分∠BAF，

∴∠OAD＝∠FAD，

∴∠ODA＝∠FAD，

∴OD∥AF，

∵DE⊥AF，

∴DE⊥OD，

又∵OD是⊙O的半径，

∴DE与⊙O相切；

（2）解：连接BD，如图2所示：

∵AB是⊙O的直径，

∴∠ADB＝90°，

∵DE⊥AF，

∴∠AED＝90°＝∠ADB，

又∵∠EAD＝∠DAB，

∴△AED∽△ADB，

∴AD：AB＝AE：AD，

∴AD2＝AB×AE＝10×8＝80，

在Rt△AED中，由勾股定理得：DE＝ ＝＝4；

（3）连接DF，过点D作DG⊥AB于G，如图3所示：

在△AED和△AGD中，，

∴△AED≌△AGD（AAS），

∴AE＝AG，DE＝DG，

∵∠FAD＝∠DAB，

∴，

∴DF＝DB，

在Rt△DEF和Rt△DGB中，，

∴Rt△DEF≌Rt△DGB（HL），

∴EF＝BG，

∴AB＝AG+BG＝AF+EF＝AF+EF+EF＝AF+2EF，

即：x+2y＝10，

∴y＝﹣x+5，

∴AE•EF＝﹣x2+5x＝﹣（x﹣5）2+，

∴AF•EF有最大值，当x＝5时，AF•EF的最大值为．

25．

解：（1）∵抛物线的顶点为（1，﹣4），

∴设抛物线的解析式为y＝a（x﹣1）2﹣4，

将点C（0，﹣3）代入抛物线y＝a（x﹣1）2﹣4中，得a﹣4＝﹣3，

∴a＝1，

∴抛物线的解析式为y＝a（x﹣1）2﹣4＝x2﹣2x﹣3；

（2）由（1）知，抛物线的解析式为y＝x2﹣2x﹣3，

令y＝0，则x2﹣2x﹣3＝0，

∴x＝﹣1或x＝3，

∴B（3，0），A（﹣1，0），

令x＝0，则y＝﹣3，

∴C（0，﹣3），

∴AC＝，

设点E（0，m），则AE＝，CE＝|m+3|，

∵△ACE是等腰三角形，

∴①当AC＝AE时，＝，

∴m＝3或m＝﹣3（点C的纵坐标，舍去），

∴E（3，0），

②当AC＝CE时，＝|m+3|，

∴m＝﹣3±，

∴E（0，﹣3+）或（0，﹣3﹣），

③当AE＝CE时，＝|m+3|，

∴m＝﹣，

∴E（0，﹣），

即满足条件的点E的坐标为（0，3）、（0，﹣3+）、（0，﹣3﹣）、（0，﹣）；

（3）如图，存在，∵D（1，﹣4），

∴将线段BD向上平移4个单位，再向右（或向左）平移适当的距离，使点B的对应点落在抛物线上，这样便存在点Q，此时点D的对应点就是点P，

∴点Q的纵坐标为4，

设Q（t，4），

将点Q的坐标代入抛物线y＝x2﹣2x﹣3中得，t2﹣2t﹣3＝4，

∴t＝1+2或t＝1﹣2，

（1+2，4）或（1﹣2，4），

分别过点D，Q作x轴的垂线，垂足分别为F，G，

∵抛物线y＝x2﹣2x﹣3与x轴的右边的交点B的坐标为（3，0），且D（1，﹣4），

∴FB＝PG＝3﹣1＝2，

∴点P的横坐标为（1+2）﹣2＝﹣1+2或（1﹣2）﹣2＝﹣1﹣2，

即P（﹣1+2，0）、Q（1+2，4）或P（﹣1﹣2，0）、Q（1﹣2，4）．