【期末总复习】人教A版(2019)高二数学选择性必修第二册——专题07 导数的应用（知识梳理）

这是一份【期末总复习】人教A版(2019)高二数学选择性必修第二册——专题07 导数的应用（知识梳理），文件包含期末总复习人教A版2019高二数学选择性必修第二册专题07导数的应用知识梳理解析版doc、期末总复习人教A版2019高二数学选择性必修第二册专题07导数的应用知识梳理原卷版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
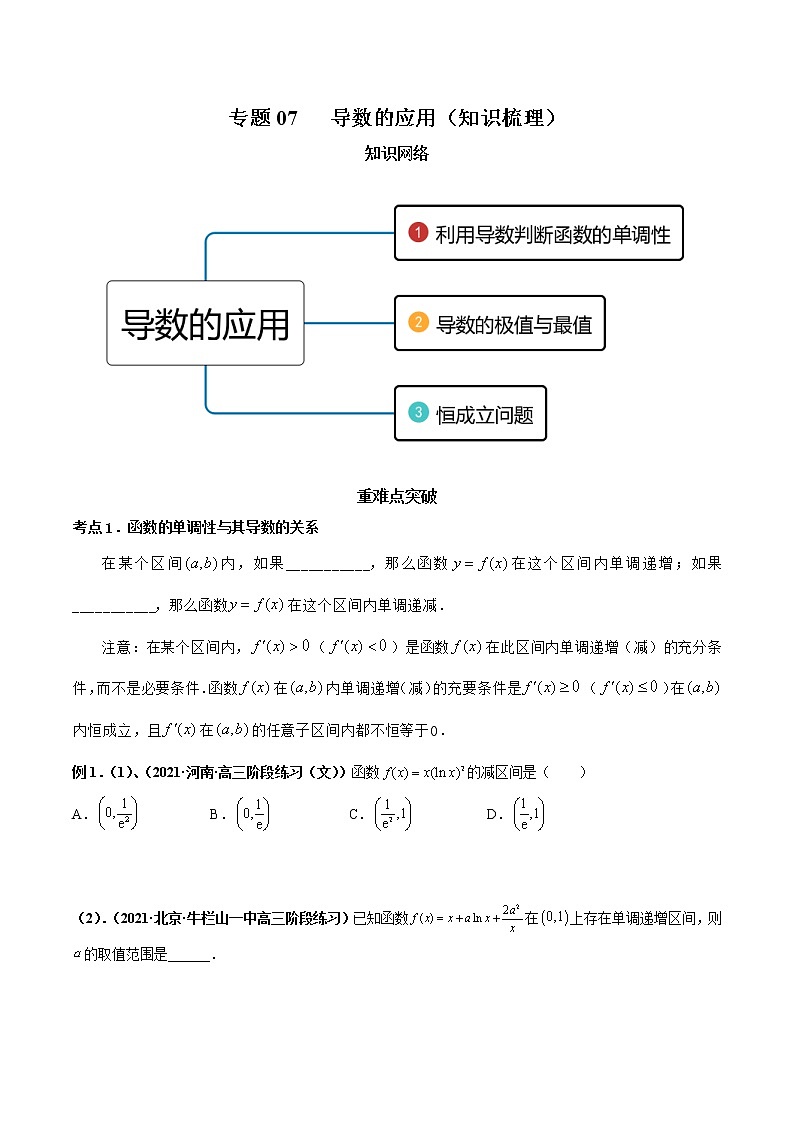
专题07   导数的应用（知识梳理）知识网络重难点突破考点1．函数的单调性与其导数的关系在某个区间内，如果___________，那么函数在这个区间内单调递增；如果___________，那么函数在这个区间内单调递减．注意：在某个区间内，（）是函数在此区间内单调递增（减）的充分条件，而不是必要条件．函数在内单调递增（减）的充要条件是（）在内恒成立，且在的任意子区间内都不恒等于0．例1．（1）、（2021·河南·高三阶段练习（文））函数的减区间是（    ）A． B． C． D．【答案】C【分析】求得，根据减函数有求减区间即可.【详解】由题意，，令，得，则，故的减区间是.故选：C（2）．（2021·北京·牛栏山一中高三阶段练习）已知函数在上存在单调递增区间，则的取值范围是______．【答案】【分析】由在上存在单调递增区间，在有解，则求解即可．【详解】因为在上存在单调递增区间，所以在有解，令，则，得故答案为：.【变式训练1-1】、（2021·全国·高二课时练习）若函数在区间内是增函数，则实数a的取值范围是______．【答案】【分析】等价于在上恒成立，再求函数的最值得解.【详解】因为函数在区间内是增函数，所以在上恒成立，故在上恒成立，则．故答案为： 【变式训练1-2】、（2021·浙江·高二单元测试）若函数在区间内存在单调递增区间，则实数的取值范围是(    )A． B．C． D．【答案】D【分析】利用导数研究函数的单调性，f(x)在内存在单调增区间，等价于在上有有解，然后参变分离即可求解﹒【详解】∵函数在区间内存在单调递增区间，∴在区间上有解(成立)，即在区间上成立，又函数在上单调递增，∴函数在上单调递增，故当时，取最小值，即，即，得．故选：D﹒例2．（2021·广东江门·高三阶段练习）已知函数.（1）当时，求的单调区间；（2）若有两个零点，且，证明.【答案】（1）单调增区间是，单调减区间是（2）证明见解析【分析】（1）当时，，结合导数正负判断函数单调区间即可；（2）因是函数零点，得，分离得，令，构造，代换成关于的函数表达式，通过求出最值，进而得证.（1）当时，,令得，令得，的单调增区间是，单调减区间是；（2）若有两个零点，则，得.，令，则，得，则，令，则，令，则，在上单调递增，.，则在上单调递增，，即，.【变式训练2-1】、（2021·安徽·合肥市第八中学高三阶段练习（文））已知函数．（1）讨论函数在上的单调性；（2）若，求证：在上恒成立.【答案】（1）答案见详解（2）证明见详解【分析】（1）求导得，令导数为0，得，再分类讨论与的位置关系即可求解；（2）当时，恒成立，令，设法证明即可.（1）由得，令得，，当时，，对恒成立，在单减；当时，，对恒成立，在单增；当时，，当，，单减；当，，单增；综上所述，当，在单减；当，在单增；当，当，单减；当，单增；（2）若，则，在上恒成立，即对恒成立，令，则，令得，当时，，单增；当时，，单减，所以，令，则，又，即，故，构造函数，又，设，，当，，单增，当，，单减，故（得证），所以，，令，在单增，，所以，所以在上恒成立.
考点2．函数极值的概念若函数在点的函数值比它在点附近其他点的函数值都小，；而且在点附近的左侧________，右侧________，就把点叫做函数的极小值点，叫做函数的极小值．若函数在点的函数值比它在点附近其他点的函数值都大，；而且在点附近的左侧________，右侧________，就把点叫做函数的极大值点，叫做函数的极大值．极大值点和极小值点统称为极值点，极大值和极小值统称为极值．例3．（1）、（2021·全国·高二课时练习）函数的极小值为______．【答案】－3【分析】求导得到，得到函数单调区间，求得极小值.【详解】因为，故，令得到，故函数在上单调递减；令得到或，故函数在和上单调递增.故极小值为.故答案为：.（2）、（2021·云南·高三阶段练习（文））已知为函数的极小值点，则（    ）A．1 B．2 C．3 D．【答案】B【分析】利用导数求出的单调性即可.【详解】，所以当时，当时则在和上单调递增，在上单调递减，故.故选：B（3）．（2021·江苏海安·高三期中）（多选题）已知函数在处取得极值，则（    ）A． B． C． D．【答案】ABC【分析】求导得到导函数，再次求导证明单调递增，根据零点存在定理得到，AB正确，代换得到，C正确，若D成立得到，矛盾，得到答案.【详解】，则，恒成立，故单调递增， ，，故存在，函数在上单调递减，在上单调递增，AB正确；，，，故C正确；若，，则，，，则，这与矛盾，故D错误.故选：ABC.    【变式训练3-1】、（2021·四川·威远中学校高三阶段练习（理））已知函数(且，)的一个极值点为2，则的最小值为（    ）A． B．C． D．7【答案】B【分析】求出函数的导数，由给定极值点可得a与b的关系，再借助“1”的妙用求解即得.【详解】对求导得：，因函数的一个极值点为2，则，此时，，，因，即，因此，在2左右两侧邻近的区域值一正一负，2是函数的一个极值点，则有，又，，于是得，当且仅当，即时取“=”，所以的最小值为.故选：B【变式训练3-2】、（2021·山东省胶州市第一中学高三阶段练习）（多选题）已知函数，则下列说法正确的是（    ）A．只有一个极值点 B．设，则与的单调性相同C．在上单调递增 D．有且只有两个零点【答案】ACD【分析】利用的二次求导，得到， ，从而存在，使得，结合函数极值点的定义即可判断选项，求出的解析式，然后利用导数研究其单调性即可判断选项，利用函数单调性的结论即可判断选项．利用函数的极值点即可判断选项.【详解】解：由题知，，，所以在上单调递增，当时，；当时，，所以存在，使得，所以函数在上单调递减，在上单调递增，所以有且只有一个极值点，故A正确；因为，所以，所以，所以，故的一个极值点为0，所以与的单调性不相同，故B错误；因为与在上都是单调递增，所以在上单调递增，故C正确；因为有且只有一个极值点，，且，所以在和上各有一个零点，所以有且只有两个零点，故D正确．故选：ACD．【变式训练3-3】、（2021·江苏南通·高三期中）已知函数，当时，有极大值.写出符合上述要求的一个的值为_________.【答案】4（答案不唯一，满足即可）【分析】由极大值的概念及求导法则即可求解【详解】由题意得，，令,解得
或，当即时，在上单调递增，在上单调递减，所以在处取极大值，所以的一个取值可取，故答案为：4（答案不唯一，满足即可）.
考点3．函数最值1．函数的最值与导数一般地，如果在区间上函数的图象是一条________的曲线，那么它必有最大值与最小值．2．求函数最值的步骤求函数在上的最大值与最小值的步骤如下：（1）求函数在内的________；（2）将函数的各极值与端点处的函数值比较，其中最大的一个是最大值，最小的一个是最小值．例4．（1）、（2021·全国·高二课时练习）已知函数（a是常数）在上有最大值3，那么它在上的最小值为（    ）A． B． C． D．【答案】D【分析】求导得到函数的单调区间得到函数最大值为，再比较端点值的大小得到最小值.【详解】，由得或，故函数在上单调递增；由得，故函数在上单调递减，故函数的最大值为．故．又，，故当时，函数取得最小值为-37．故选：D.（2）．（2021·福建·模拟预测）（多选题）已知函数，下列说法正确的是（    ）A．当时，；当时，B．函数的减区间为，增区间为C．函数的值域D．恒成立【答案】ACD【分析】由对数函数的性质直接判断A，利用导数确定函数的单调性与极值判断BC，D选项中，不等式变形为，然后引入函数，由导数求得最小值判断D．【详解】对于选项A，当时，；当时，，故选项A正确；对于选项B，，令可得，有，可知函数的减区间为，增区间为，故选项B错误；对于选项C，由上可知，时，，故选项C正确；对于选项D，，令，有，令可得，故函数的增区间为，减区间为，可得，故选项D正确．故选：ACD．【变式训练4-1】、（2021·全国·高二课时练习）（多选）已知函数，则（    ）A．在处取得极大值 B．有两个不同的零点C．的极小值点为 D．【答案】AD【分析】的定义域为，求判断单调性，求得极值可判断A，C；根据单调性以及可判断B、D，进而可得正确选项.【详解】由题意可得函数的定义域为，由可得，令，解得：当时，，则在上单调递增；当时，，则在上单调递堿．所以当时，函数取得极大值为，无极小值，故选项A正确，选项C不正确；因为，且在上单调递增，所以函数在上有一个零点．当时，，，所以，此时无零点．综上所述：有一个零点，故B不正确；因为，在上单调递增，所以，故选项D正确．故选：AD．  【变式训练4-2】、（2021·浙江·高三期中）已知函数在上的最大值为3，则实数a的所有取值组成集合为（    ）A． B．C． D．【答案】C【分析】根据最值的性质，结合任意性和存在性的性质进行求解即可.【详解】由在上的最大值为3，则对恒成立，且至少存在一个，使等号成立．即对恒成立，且至少存在一个，使等号成立．若恒成立，可化为对恒成立，且至少存在一个，使等号成立．所以，或，显然函数在上是增函数，因此当时，有最大值为，所以，当时，，此时函数递减，当时，，此时函数递增，当时，，此时函数递减，当时，，当时，，此时最小值为， 若恒成立，可化为，或对恒成立，且至少存在一个，使等号成立．所以，或，显然函数在上是增函数，因此当时，有最小值为，所以，当时，，此时函数递减，当时，，此时函数递增，当时，，此时函数递减，当时，，当时，，此时函数最大值为所以所以满足条件的a的值为，，－5，－3．故选：C【点睛】关键点睛：本题的关键是对最值的概念的理解.例5．（2021·全国·高三阶段练习（文））已知函数.（1）讨论函数的极值；（2）若函数在上的最小值是，求实数的值.【答案】（1）答案见解析（2）【分析】（1）求得，分和两种情况讨论，结合导数的符号，即可求解；（2）由（1）知，当时，不符合题意；当时，分、和三种情况讨论，结合函数的单调性和，即可求解.（1）解：由题意，函数的定义域为，可得，当时，可得，单调递增，此时函数的无极值；当时，令，可得，当时，，单调递减；当时，，单调递增，所以当时，函数取得极小值，极小值为，无极大值.综上所述，当时，函数的无极值；当时，函数的极小值为，无极大值.（2）由（1）知，当时，单调递增，可得，即（舍去）；当时，函数在上单调递减，上单调递增，若时，即时，函数在上单调递增，所以，解得（舍去）若时，即时，函数在上单调递减，可得，解得（舍去），若时，即时，在上单调递减，在上单调递增，可得，即，解得，综上可得，实数的值为.【变式训练5-1】、（2020·天津市南开区南大奥宇培训学校高三阶段练习）已知函数．（1）若f(x)在(–1，f(–1))处的切线方程为，求a，k的值；（2）求f(x)的单调递减区间；（3）若f(x)在区间[–2，2]上的最大值为20，求它在该区间上的最小值．【答案】（1）（2）和（3）【分析】（1）利用切点和斜率求得.（2）利用导数求得的单调递减区间.（3）分析在区间上的极值以及区间端点的函数值，结合最大值为求得，进而求得最小值.（1）因为，所以，由题设可得，解得.（2）令，解得或，所以函数f(x)的单调递减区间为和．（3）因为，所以．因为在上，所以f(x)在[– 1，2]上单调递增，又由于f(x)在[– 2，– 1]上单调递减，因此f(2)和f(– 1)分别是f(x)在区间[– 2，2]上的最大值和最小值．于是有22+a=20，解得．故.因此，即函数f(x)在区间[– 2，2]上的最小值为– 7． 
考点4．恒成立问题不等式恒成立问题常见处理方法：① 分离参数恒成立(可)或恒成立（即可）；② 数形结合(图象在 上方即可)；③ 讨论最值或恒成立；④ 讨论参数.例6．（2021·黑龙江·哈尔滨市呼兰区第一中学校高三阶段练习（文））已知的图象在点处的切线与直线平行.（1）求a，b满足的关系式；（2）若在上恒成立，求a的范围.【答案】（1）（2）【分析】（1）求导，利用计算求解即可；（2）令，求导可得，分，，讨论，研究的单调性及最值，进而可得a的范围.（1）求导函数可得，根据题意，即（2）解：由（1）知，，令，i）当时，，在上单调递减，∴，舍.ii）当时，令或，①当时，，若，则，若，则，在上是减函数，在上是增函数，所以在上，，即在上不恒成立.②时，，当时，，在增函数，又，所以.综上所述，所求a的取值范围是例7．（2021·江苏如皋·高三期中）已知函数，.（1）当时，求函数的最大值；（2）若关于的不等式对任意的实数恒成立，其中为自然对数的底数，求的取值范围.【答案】（1）：（2）.【分析】（1）代入，然后求导，通过导函数来判断原函数单调性，最后简单计算可得结果.（2）对、进行讨论，然后通过对式子化简变形分离参数，进一步使用不等式，最后简单判断即可.（1）当时，，，令，且当时，，↗；当时，，↘，∴.（2）对任意的恒成立，即对恒成立，当时，显然成立.当时，，由，当且仅当，时取“”，∴取不到“”，即，∴，的取值范围为.