浙江省金华市2021-2022学年九年级上学期期中数学试题(含答案)

2021-2022 学年第一学期九年级数学分层知识演练（二）

一、选择题 （本题有 10 小题，每小题 3 分，共 30 分）

1．（★）已知⊙O的半径为6，点A与圆心O的距离为5，则点A与⊙O的位置关系是（    ）

A．点A在⊙O外  B．点A在⊙O内  C．点A在⊙O上  D．无法确定

2．（★）从“绿水青山就是金山银山”中任选一个字，选中“山”的概率是（    ）

A．     B．     C．     D．

3．（★）抛物线y=x2－4x－4的开口方向、对称轴和顶点坐标分别是（）

A．开口向上，对称轴是直线，顶点坐标是

B．开口向上，对称轴是直线，顶点坐标是

C．开口向上，对称轴是直线，顶点坐标是

D．开口向下，对称轴是直线，顶点坐标是

4．（★）已知，为抛物线上的两点，则下列结论一定成立的是（    ）

A．   B．   C．   D．

5．（★）如图，在平面直角坐标系中，点A，B，C的坐标分别为，，，则以A，B，C为顶点的三角形的外接圆的圆心坐标是（    ）

A．    B．    C．    D．

6．（★）如图，A，B，C为⊙O上的三点，若∠ABO=20°，∠ACO=30°，则∠BOC的度数为（     ）

A．100°     B．110°     C．125°     D．130°

7．（★★）如图，四边形ABCD为⊙O的内接四边形，AB为⊙O的直径，若∠AOD=40°，弦AC平分∠DAB，则∠ADC的度数为（    ）

A．140°     B．125°     C．110°     D．105°

8．（★★）下列四个命题：①在同圆或等圆中，相等的弦所对的弧相等；②在同圆或等圆中，相等的弧所对的弦相等；③在同圆或等圆中，相等的弦的弦心距相等；④在同圆或等圆中，相等的弧所对的圆心角相等，其中真命题有（    ）

A．1个     B．2个     C．3个     D．4个

9．（★★）如图，将边长为1的正六边形ABCDEF放置于平面直角坐标系中，使边AB在x轴的正半轴上，顶点F在y轴的正半轴上，将正六边形ABCDEF绕坐标原点O顺时针旋转，每次旋转60°，那么经过第2025次旋转后，顶点D的坐标为（    ）

A．   B．   C．   D．

10．（★★★）如图，在平面直角坐标系中，顶点坐标为的抛物线经过点，与y轴的交点在和之间（含端点），则下列结论：①；②；③；④关于x的方程有两个不相等的实数根，其中正确的结论有（    ）

A．1个     B．2个     C．3个     D．4个

二、填空题 （本题有 6 小题，每小题 4 分，共 24 分）

11．（★）二次函数的图象与y 轴的交点坐标是         ．

12．（★）从一副扑克牌中任意抽取1张，则下列事件：①抽取的这张牌是“8”；②抽取的这张牌是“方块”；③抽取的这张牌是“小王”；④抽取的这张牌是“黑色的”，按其发生的可能性的大小从小到大用“<”排列为______．

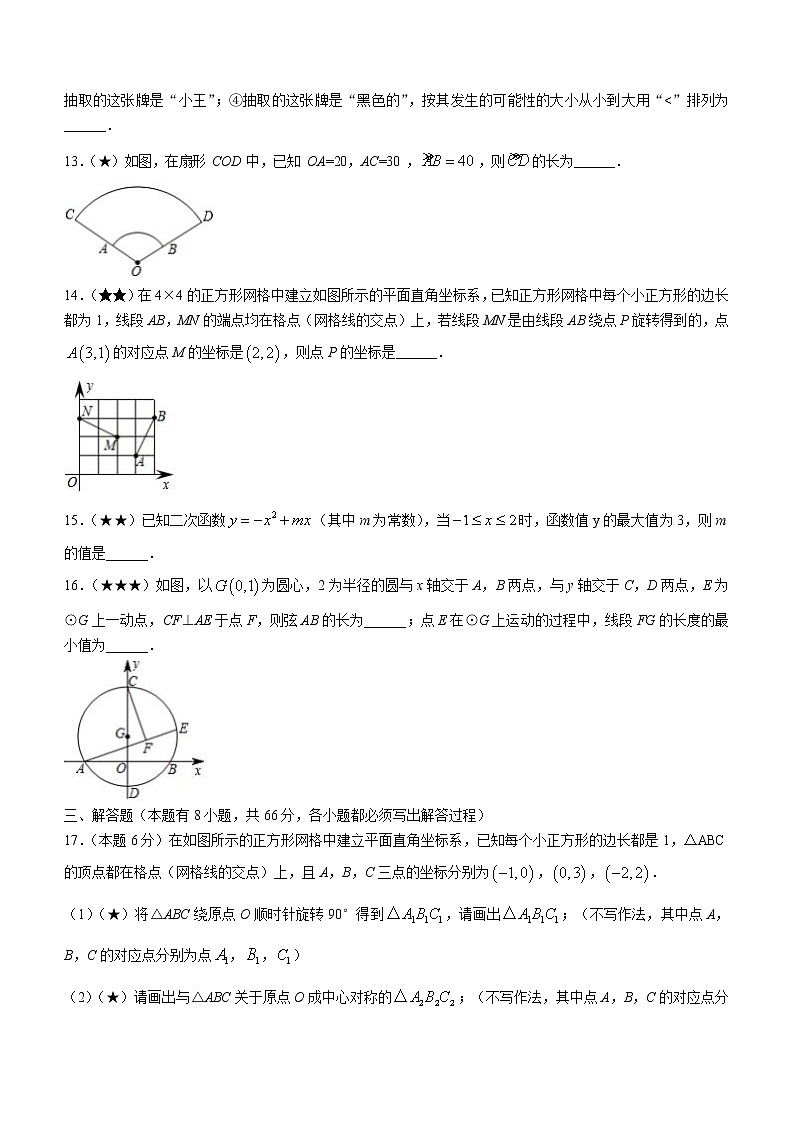
13．（★）如图，在扇形 COD 中，已知 OA=20，AC=30 ，，则的长为______．

14．（★★）在4×4的正方形网格中建立如图所示的平面直角坐标系，已知正方形网格中每个小正方形的边长都为1，线段AB，MN的端点均在格点（网格线的交点）上，若线段MN是由线段AB绕点P旋转得到的，点的对应点M的坐标是，则点P的坐标是______．

15．（★★）已知二次函数（其中m为常数），当时，函数值y的最大值为3，则m的值是______．

16．（★★★）如图，以为圆心，2为半径的圆与x轴交于A，B两点，与y轴交于C，D两点，E为⊙G上一动点，CF⊥AE于点F，则弦AB的长为______；点E在⊙G上运动的过程中，线段FG的长度的最小值为______．

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

17．（本题6分）在如图所示的正方形网格中建立平面直角坐标系，已知每个小正方形的边长都是1，△ABC的顶点都在格点（网格线的交点）上，且A，B，C三点的坐标分别为，，．

（1）（★）将△ABC绕原点O顺时针旋转90°得到，请画出；（不写作法，其中点A，B，C的对应点分别为点，，）

（2）（★）请画出与△ABC关于原点O成中心对称的；（不写作法，其中点A，B，C的对应点分别为，，）

（3）（★）连结，，求四边形的面积．

18．（★★）（本题6分）现有四张扑克牌（方块2、黑桃4、黑桃5、梅花5）的牌面如图1所示，将扑克牌洗匀后，按图2所示背面朝上放置在桌面上．小亮和小明设计的游戏规则是两人同时任意抽取一张扑克牌，若两张牌面的数字之和为奇数，则小亮获胜；否则小明获胜．请问这个游戏规则是否公平？并说明理由．

19．（本题6分）如图，AB是⊙O的直径，C，D是⊙O上的两点，过点O作，交AD于点E，连结BC．

（1）（★）求证：；

（2）（★★）若AB=6，∠ABC=30°，求图中阴影部分的面积．

20．（本题8分）在体育课训练期间，小亮在练习实心球项目时，发现实心球的飞行路线是一条抛物线（不计空气阻力），如图为实心球的飞行高度y（m）与水平距离x（m）之间的函数关系图象，其中抛物线最高点的坐标为，请根据图象解答下列问题：

（1）（★）小亮在训练过程中实心球飞行的最远距离为______m；

（2）（★）求实心球的飞行高度y（m）与水平距离x（m）之间的函数表达式；

（3）（★★）当时，求对应的x的值，并解释它们的实际意义．

21．（本题8分）新型冠状病毒肺炎疫情爆发后，某校积极响应教育部“停课不停学”的号召，认真组织各科教师进行在线教育，其中体育组以学科课程标准为蓝本，将体育课的教学内容统筹划分为：“A．国粹之武”、“B．球类竞技”、“C．魅力舞蹈”、“D．田径之美”、“E．健身健美”五个版块．小张老师为了解学生们对体育网课课程版块的偏好，在全校范围内，对学生们最喜爱的体育版块进行了调查，并随机抽取了部分调查结果，绘制出如图所示的两幅不完整的统计图．

请根据图中提供的信息，解答下列问题：

（1）（★）补全条形统计图；

（2）（★）______，在扇形统计图中，“A”所占圆心角的度数为______；

（3）（★）在随机抽取的调查结果中，任选一份，恰好选到学生选择的是“C．魅力舞蹈”版块的概率是多少？

（4）（★）若该校共有2700名学生，请估计学生最喜爱的体育网课板块是“B．球类竞技”的人数．

22．（本题10分）2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件，每销售一件需缴纳网络平台管理费2元，为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．

（1）（★）求每天的销售量y（件）与销售单价x（元）之间的函数关系式；

（2）（★★）当销售单价为多少元时，销售这款文化衫每天所获得的利润最大，最大利润为多少元？

23．（本题10分）在平面直角坐标系xOy中，O为坐标原点，，为坐标系内不重合的两点，若P，Q为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x轴或y轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点P与点Q之间的“折距”，记作或．例如：如图，，，此时．特别地，当PQ与某条坐标轴平行（或重合）时，线段PQ的长即为点P与点Q之间的“折距”．

请根据上述定义，解答下列问题：

（1）①（★）若点，则______；

②（★★）若点Q是以O为圆心，1为半径的⊙O上的任意一点，则的最小值是______；

（2）（★★）若一次函数的图象分别与x轴，y轴于A，B两点，点P是线段AB上的一点，求的值；

（3）（★★）若，点N是以为圆心，1为半径的⊙T上的任意一点，若存在一点N满足，请直接写出t的取值范围．

24．（本题12分）如图，抛物线与x轴交于，两点，与y轴交于点，M是该抛物线的顶点．

（1）（★）求抛物线的函数表达式和点M的坐标；

（2）（★★）在抛物线上A，C两点之间的部分（不包含A，C两点），是否存在一点D，使得？若存在，请求出点D的横坐标；若不存在，请说明理由；

（3）（★★★）若E是x轴上的一个动点，F为平面直角坐标系内的一点，当以A，C，E，F为顶点的四边形为菱形时，请求出满足条件的点E的坐标．

2021-2022学年第一学期九年级数学分层知识演练（二）

参考答案

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

11．  12．③＜①＜②＜④  13．100   14． 

15．或  16． 

三、解答题（本题有8小题，共66分，各小题都必须写出解答过程）

17．（本题6分）

解：（1）如图，即为所求．

（2）如图，即为所求．

（3）∵，

∴四边形为菱形．又∵，，∴．

18．（本题6分）

解：这个游戏规则不公平．理由如下：

根据题意，画树状图如下：

由树状图可知，共有12种等可能的结果，其中两张牌面的数字之和为奇数的结果由8种，

∴P（小亮获胜）；P（小明获胜），

∵，∴这个游戏规则不公平．

19．（本题6分）

（1）证明：∵AB是⊙O的直径，∴．

∵，∴，即．

又∵OC为⊙O的半径，∴．

（2）解：如图，连结CD，OD，

∵，，∴．

∴．∵由（1）可知，

∴．∴．∴．

∴．∵，由（1）可知，

∴．∴在中，由勾股定理，得

．∵，，∴．

∴．

20．（本题8分）

解：（1）10

（2）∵抛物线最高点的坐标为，

∴设实心球的飞行高度y（m）与水平距离x（m）之间的函数表达式为

，把代入，得，解得，

∴．

（3）当时，，解得，．

实际意义：当水面距离为1m或7m时，实心球的飞行高度为2.25m．

21．（本题8分）

解：（1）补全条形统计图如下：

【解法提示】∵被抽取的学生总数为（人），

∴最喜爱C版块的学生有（人）．

（2）14  43.2°

【解法提示】，∴，

在扇形统计图中，“A”所占圆心角的度数为．

（3）∵在随机抽取的调查结果中，任选一份，共有50种等可能的结果，

其中恰好选到学生选择的是“C．魅力舞蹈”版块的结果有14种，

∴P（恰好选到学生选择的是“C．魅力舞蹈”版块）．

（4）（人）

答：估计学生最喜爱的体育网课版块是“B．球类竞技”的有972人．

22．（本题10分）

解：（1）由题意，得，整理，得，

∴每天的销售量y（件）与销售单价x（元）之间的函数关系式为．

（2）设所获得的利润为w元，由题意，得

，

整理，得，∵，

∴当时，w取最大值，最大值为1152，

∴当销售单价为56元时，销售这款文化衫每天所获得的利润最大，最大利润为1152元．

23．（本题10分）

解：（1）①3   ②1

【解法提示】①如图，∵点，

∴以点O，P为锐角顶点的的两条直角边长分别为1，2，∴．

②∵点Q是以O为圆心，1为半径的⊙O上的任意一点，

∴当OQ与x轴或y轴重合时，的值最小，最小值为1．

（2）∵一次函数的图象分别与x轴，y轴于A，B两点，

∴，．∵点P是线段AB上一点，

∴设，则，，∴．

（3）t的取值范围为或．

【解法提示】如图，

当点N在⊙T最上方，即轴时，

∵点，，∴或．

此时或，若或，则．

∴．又∵当时，M、N均在⊙T上，

此时的最大值为2，综上所述，t的取值范围为或．

24．（本题12分）

解：（1）∵抛物线与x轴交于，两点，

∴设抛物线的函数表达式为，

将代入，得，解得，

∴，∴．

∴抛物线的函数表达式为，点M的坐标为．

（2）存在．设直线AC的函数表达式为，

将，代入，得，解得，

∴直线AC的函数表达式为．

如图，过点D作轴交直线AC于点G，过点M作轴交直线AC于点H，

设，则，

∵由（1）可知点M的坐标为，∴点H的横坐标为．

把代入，得，∴．

∴，．

∴．

同理可得．∵，∴，即，

解得，，∴点D的横坐标为或．

（3）设，∵，

∴，，,

①当CE为菱形的对角线时，则，

∴，即，解得，，

∴点E的坐标为或；

②当AC为菱形的对角线时，则，∴，

即，解得，∴点E的坐标为；

③当AE为菱形的对角线时，则，∴，

即，解得（舍去），，

∴点E的坐标为．综上所述，当点E的坐标为

或或或时，以A，C，E，F为顶点的四边形为菱形．