





第14讲二次函数的图象及其性质(导学案+教案+精炼)
展开第14讲二次函数的图象及其性质
一、知识梳理
二次函数的概念
定义 | 一般地,如果____________ (a,b,c是常数,a≠0),那么y叫做x的二次函数 |
二次函数 y=ax2+bx+c 的结构特征 | ①等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2; ②二次项系数a≠0 |
二次函数的图象及画法
图象 | 二次函数y=ax2+bx+c(a≠0)的图象是以____________为顶点,以直线______________为对称轴的抛物线 |
用描点法画 二次函数 y=ax2+bx+c 的图象的步骤 | (1)用配方法化成________________的形式; (2)确定图象的开口方向、对称轴及顶点坐标; (3)在对称轴两侧利用对称性描点画图 |
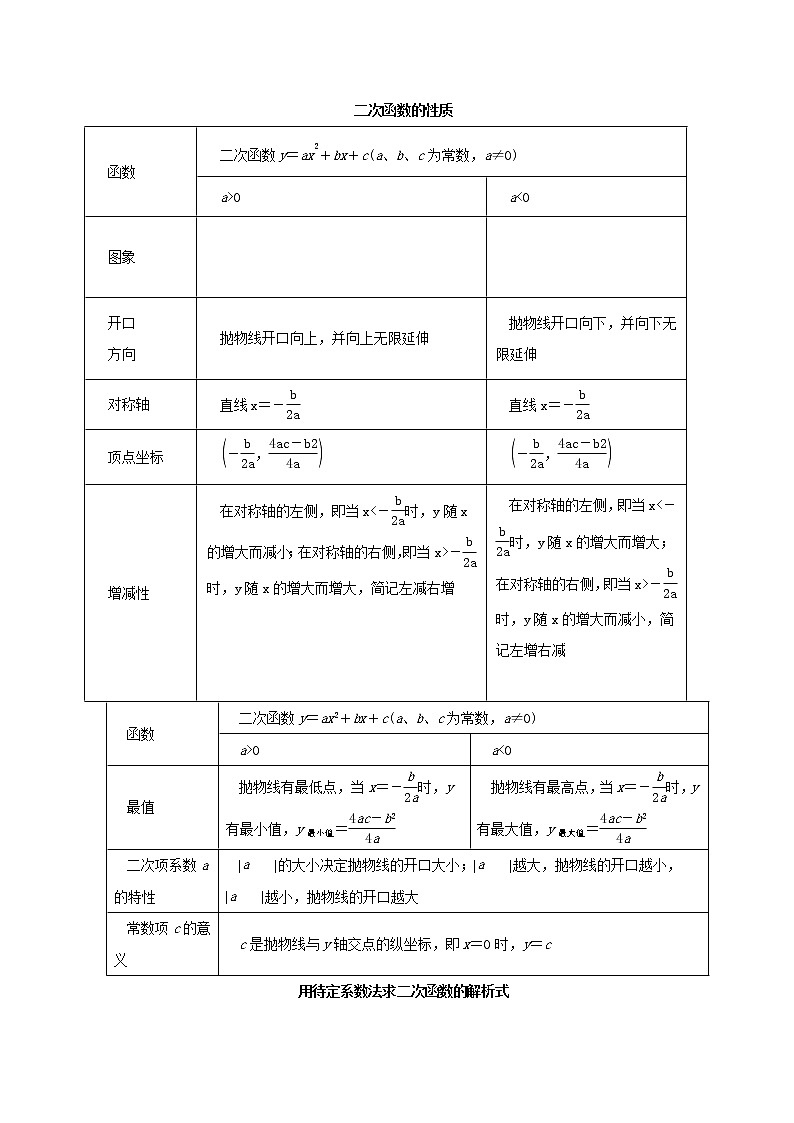
考点3 二次函数的性质
函数 | 二次函数y=ax2+bx+c(a、b、c为常数,a≠0) | |||||
a>0 | a<0 | |||||
图象 | ______________ | ______________ | ||||
开口 方向 | 抛物线开口向上,并向上无限延伸 | 抛物线开口向下,并向下无限延伸 | ||||
对称轴 | 直线x=- | 直线x=- | ||||
顶点坐标 | ||||||
增减性 | 在对称轴的左侧,即当x<-时,y随x的增大而减小;在对称轴的右侧,即当x>-时,y随x的增大而增大,简记左减右增 | 在对称轴的左侧,即当x<-时,y随x的增大而增大;在对称轴的右侧,即当x>-时,y随x的增大而减小,简记左增右减
| ||||
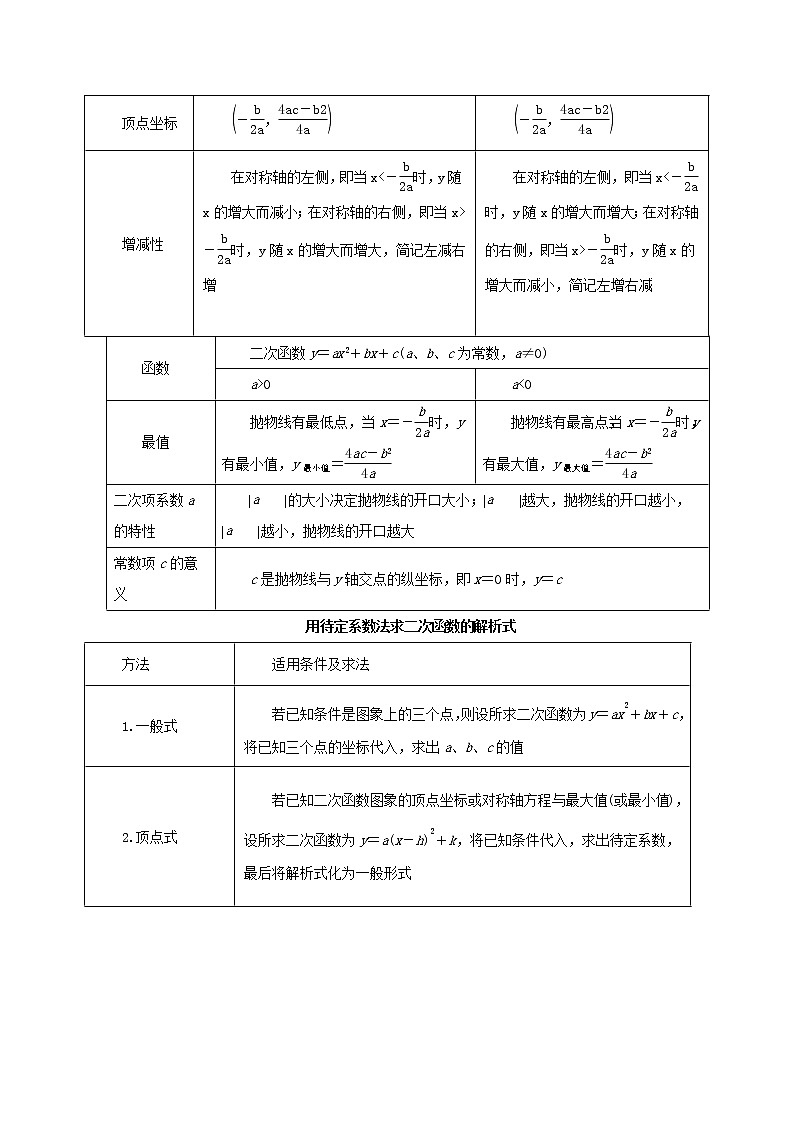
函数 | 二次函数y=ax2+bx+c(a、b、c为常数,a≠0) | |||||
a>0 | a<0 | |||||
最值 | 抛物线有最低点,当x=-时,y有最小值,y最小值= | 抛物线有最高点,当x=-时,y有最大值,y最大值= | ||||
二次项系数a的特性 | 的大小决定抛物线的开口大小;越大,抛物线的开口越小,越小,抛物线的开口越大 | |||||
常数项c的意义 | c是抛物线与y轴交点的纵坐标,即x=0时,y=c | |||||
用待定系数法求二次函数的解析式
方法 | 适用条件及求法 |
1.一般式 | 若已知条件是图象上的三个点,则设所求二次函数为y=ax2+bx+c,将已知三个点的坐标代入,求出a、b、c的值 |
2.顶点式 | 若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),设所求二次函数为y=a(x-h)2+k,将已知条件代入,求出待定系数,最后将解析式化为一般形式 |
3.交点式 | 若已知二次函数图象与x轴的两个交点的坐标为(x1,0),(x2,0),设所求二次函数为y=a(x-x1)(x-x2),将第三点(m,n)的坐标(其中m、n为已知数)或其他已知条件代入,求出待定系数a,最后将解析式化为一般形式 |
二、题型、技巧归纳
考点1二次函数的定义
例1若是二次函数,则m=( )
A.7 B.-1
C.-1或7 D.以上都不对
技巧归纳:利用二次函数的定义,二次函数中自变量的最高次数是2,且二次项的系数不为0.
考点2二次函数的图象与性质
例2
(1)用配方法把二次函数y=x2-4x+3变成y=(x-h)2+k的形式;
(2)在直角坐标系中画出y=x2-4x+3的图象;
(3)若A(x1,y1),B(x2,y2)是函数y=x2-4x+3图象上的两点,且x1<x2<1,请比较y1、y2的大小关系(直接写结果);
(4)把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来.
技巧归纳:(1)求二次函数的图象的顶点坐标有两种方法:①配方法;②顶点公式法,顶点坐标为.
(2)画抛物线y=ax2+bx+c的草图,要确定五个方面,即①开口方向;②对称轴;③顶点;④与y轴交点;⑤与x轴交点.
考点3二次函数的解析式的求法
例3 已知抛物线经过点A(-5,0),B(1,0),且顶点的纵坐标为 ,求二次函数的解析式.
技巧归纳:
二次函数的关系式有三种:
1.一般式y=ax2+bx+c;
2.顶点式y=a(x-m)2+n,其中(m,n)为顶点坐标;
3.交点式y=a(x-x1)(x-x2),其中(x1,0),(x2,0)为抛物线与x轴的交点.一般已知三点坐标用一般式求关系式;已知顶点及另一个点坐标用顶点式;已知抛物线与x轴的两个交点坐标及另一个点的坐标用交点式.此题属于第三种情形.
三、随堂检测
1、已知二次函数y=2(x-3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象的顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中说法正确的有( )
A.1个 B.2个
C.3个 D.4个
2、设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2
C.y3>y2>y1 D.y3>y1>y2
3、 小敏在今年的校运动会跳远比赛中跳出了好成绩,函数h=4.9t一3.5t2 (t的单位:s,h的单位:m)可以描述她跳跃时重心高度的变化,则她起跳后到重心最高时所用的时间是 ( )
A. 0.71 s B 0.70 s C. 0.63 s D 0.36 s
4、将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
5、二次函数的最小值是 .
6、函数取得最大值时,______.
7、 已知实数x、y满足x2-2x+4y=5,则x+2y的最大值为 .
参考答案
例1、A
例2、解:(1)y=x2-4x+3=(x2-4x+4)+3-4=(x-2)2-1.
(2)由(1)知图象的对称轴为直线x=2,顶点坐标为(2,-1),列表:
x | … | 0 | 1 | 2 | 3 | 4 |
|
y | … | 3 | 0 | -1 | 0 | 3 | … |
描点作图如下图.
(3)y1>y2.
(4)如图,点C,D的横坐标x3,x4即为方程x2-4x+3=2的根
例3、∵抛物线与x轴的两个交点为A(-5,0),B(1,0),由对称性可知,它的对称轴为直线x==-2,∴抛物线的顶点为P,已知抛物线上的三点A(-5,0),B(1,0),P,设一般式,设y=ax2+bx+c,把A(-5,0),B(1,0),P的坐标代入,得
∴ 解得
∴ 所求抛物线的关系式为y=-x2-2x+.
随堂检测
1、A
2、A
3、B
提示:利用顶点公式求解
4、12.5
提示:设分成x和(20-x)两段,则边长分别是和,得函数求最大值
5、-4
提示:利用顶点公式求解
6、
提示:先化为一般形式,再用顶点公式求解
7、
提示:由得,,,再利用顶点公式求解
第22讲相似三角形及其应用(导学案+教案+精炼): 这是一份第22讲相似三角形及其应用(导学案+教案+精炼),文件包含第22讲相似三角形及其应用doc、第22讲相似三角形及其应用教案doc、第22讲相似三角形及其应用导学案doc等3份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
第11讲一次函数的图象与性质(导学案+教案+精炼): 这是一份第11讲一次函数的图象与性质(导学案+教案+精炼),文件包含第11讲一次函数的图象与性质教案doc、第11讲一次函数的图象与性质导学案doc、第11讲一次函数的图象与性质专题精练doc等3份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
第8讲分式方程及其应用(导学案+教案+精炼): 这是一份第8讲分式方程及其应用(导学案+教案+精炼),文件包含第8讲分式方程及其应用专题精练doc、第8讲分式方程及其应用导学案doc、第8讲分式方程及其应用教案doc等3份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。












