



第19讲全等三角形(导学案+教案+精炼)
展开第19讲:全等三角形
一、夯实基础
1.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60° C.80° D.90°
2.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠BCA=∠F B.∠B=∠E
C.BC∥EF D.∠A=∠EDF
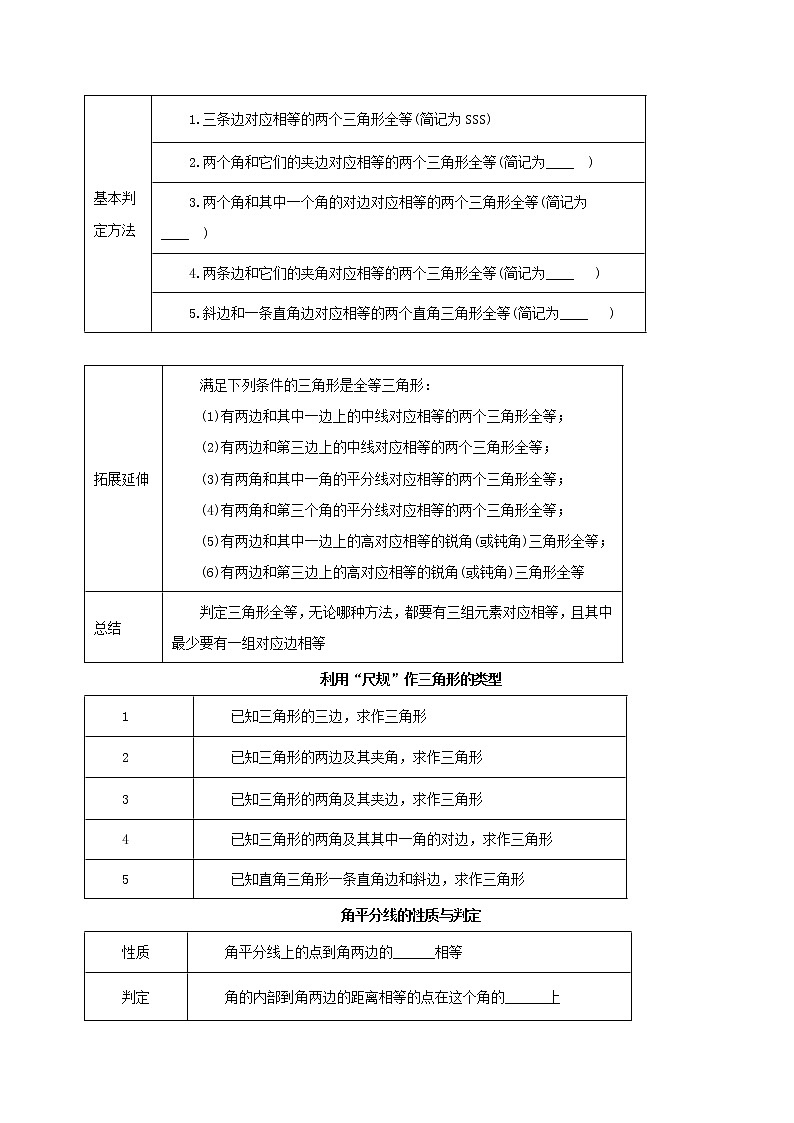
3.在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是__________.
4.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BE=CD.
5.如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE,AC.
(1)求证:△ABE≌△CDA;
(2)若∠DAC=40°,求∠EAC的度数.
二、能力提升
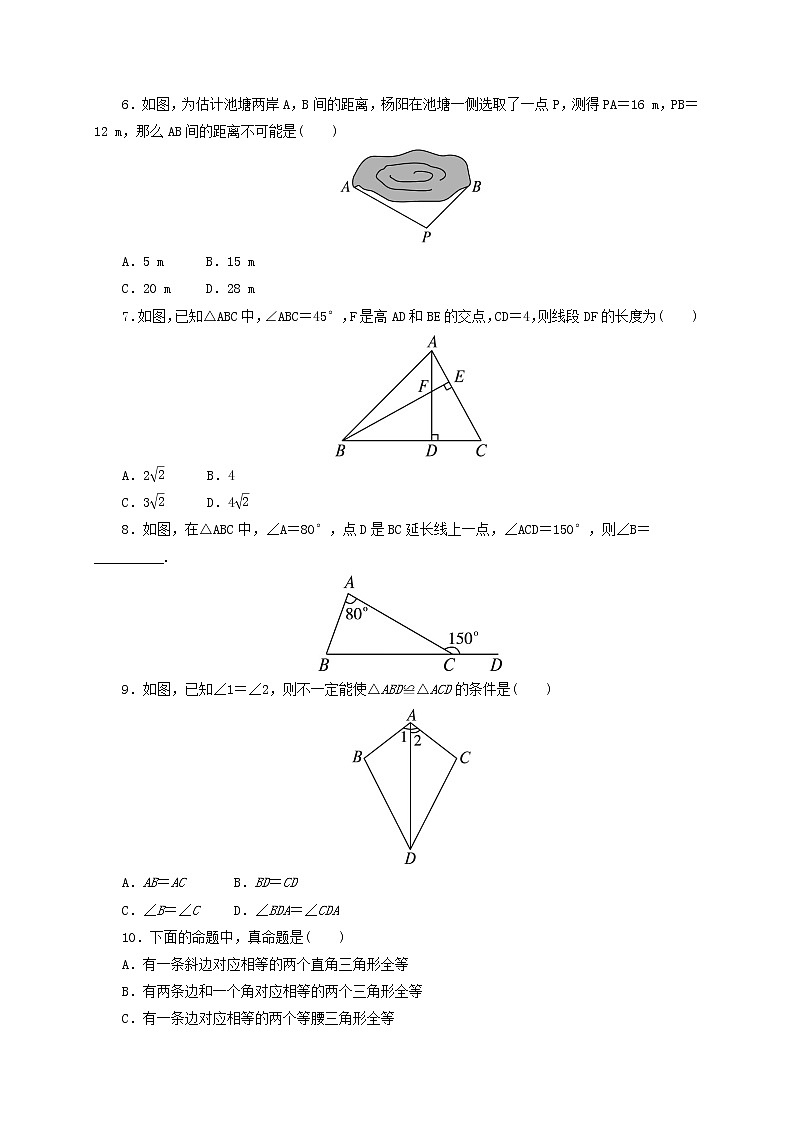
6.如图,为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16 m,PB=12 m,那么AB间的距离不可能是( )
A.5 m B.15 m
C.20 m D.28 m
7.如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
A.2 B.4
C.3 D.4
8.如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=__________.
9.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD
C.∠B=∠C D.∠BDA=∠CDA
10.下面的命题中,真命题是( )
A.有一条斜边对应相等的两个直角三角形全等
B.有两条边和一个角对应相等的两个三角形全等
C.有一条边对应相等的两个等腰三角形全等
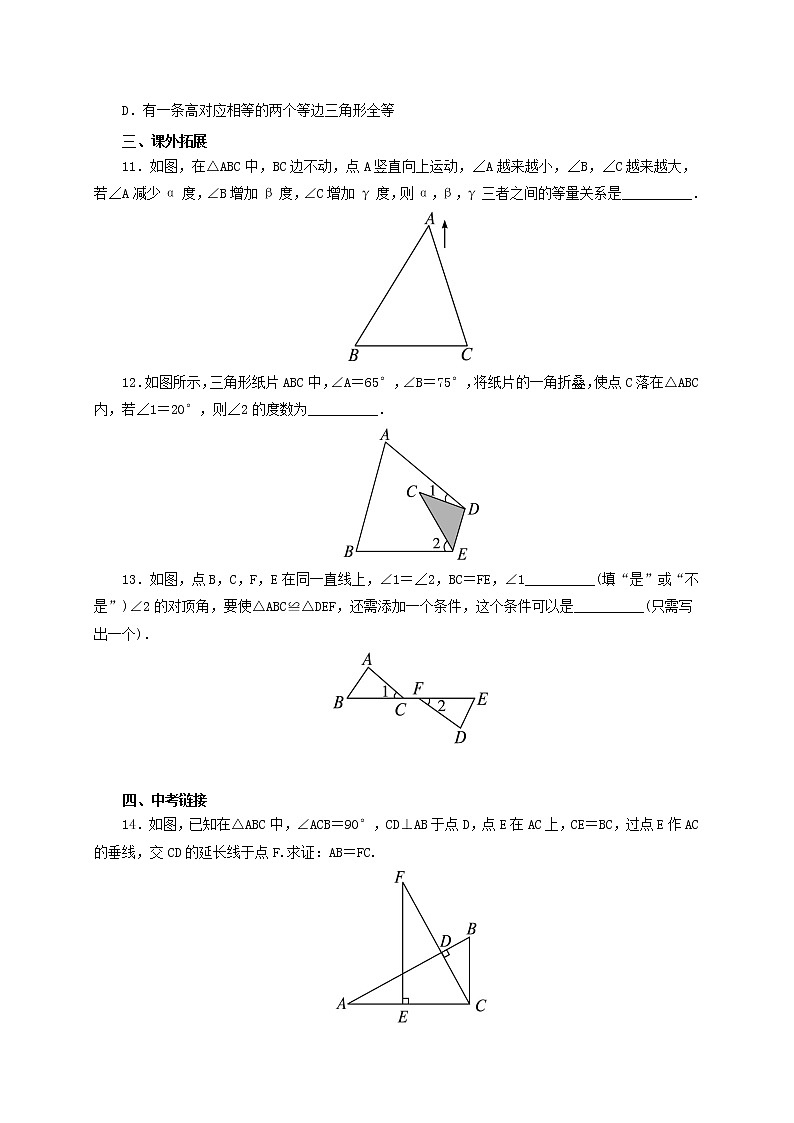
D.有一条高对应相等的两个等边三角形全等
三、课外拓展
11.如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是__________.
12.如图所示,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为__________.
13.如图,点B,C,F,E在同一直线上,∠1=∠2,BC=FE,∠1__________(填“是”或“不是”)∠2的对顶角,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是__________(只需写出一个).
四、中考链接
14.如图,已知在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过点E作AC的垂线,交CD的延长线于点F.求证:AB=FC.
15.如图,点A,B,D,E在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF.
参考答案
一、夯实基础
1.A 设∠A=x,则∠B=2x,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.
2.B由已知可得两个三角形已有两组边对应相等,还需要另一组边对应相等或夹角对应相等,只有B能满足条件.
3.①②④ 由题意知AD=AD,条件①可组成三边对应相等,条件②可组成两角和其中一角的对边对应相等,条件④可组成两边及其夹角对应相等,这三个条件都可得出△ADB≌△ADC,条件③组成的是两边及其一边的对角对应相等,不能得出△ADB≌△ADC.
4.证明:∵在△ABE和△ACD中,∠B=∠C,AB=AC,∠A=∠A,∴△ABE≌△ACD(ASA).∴BE=CD.
5.(1)证明:在梯形ABCD中,∵AD∥BC,AB=CD,
∴∠ABE=∠BAD,∠BAD=∠CDA.
∴∠ABE=∠CDA.
在△ABE和△CDA中,
∴△ABE≌△CDA.
(2)解:由(1)得∠AEB=∠CAD,AE=AC,∴∠AEB=∠ACE.
∵∠DAC=40°,∴∠AEB=∠ACE=40°.
∴∠EAC=180°-40°-40°=100°.
二、能力提升
6.D 由三角形三边关系知16-12<AB<16+12,故选D.
7.B 因为由已知可证明△BDF≌△ADC,所以DF=CD.
8.70°
9. B
10.D
三、课外拓展
11.α=β+γ
12.60° ∵∠A+∠B+∠C=180°,∠CDE+∠CED+∠C=180°,
∴∠A+∠B=∠CDE+∠CED.
∴∠A+∠B+∠CDE+∠CED=2(∠A+∠B)=280°.
∵∠1+∠2+∠CDE+∠CED+∠A+∠B=360°,
∴∠1+∠2=360°-280°=80°.
又∵∠1=20°,∴∠2=60°.
13.不是 ∠B=∠E(答案不唯一)
四、中考链接
14.证明:∵FE⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°.
∴∠F+∠ECF=90°.
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°.
∴∠A=∠F.
在△ABC和△FCE中,
∴△ABC≌△FCE.∴AB=FC.
15.证明:∵AD=EB,
∴AD-BD=EB-BD,即AB=ED.
又∵BC∥DF,∴∠CBD=∠FDB.
∴∠ABC=∠EDF.
又∵∠C=∠F,
∴△ABC≌△EDF.
∴AC=EF.
第16讲二次函数的应用(导学案+教案+精炼): 这是一份第16讲二次函数的应用(导学案+教案+精炼),文件包含第16讲二次函数的应用导学案doc、第16讲二次函数的应用教案doc、第16讲二次函数的应用专题精练doc等3份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
第13讲反比例函数(导学案+教案+精炼): 这是一份第13讲反比例函数(导学案+教案+精炼),文件包含第13讲反比例函数专题精练doc、第13讲反比例函数导学案doc、第13讲反比例函数教案doc等3份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
第12讲 一次函数的应用(导学案+教案+精炼): 这是一份第12讲 一次函数的应用(导学案+教案+精炼),文件包含第12讲一次函数的应用导学案doc、第12讲一次函数的应用教案doc、第12讲一次函数的应用专题精练doc等3份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。