河南省郑州市第四初级中学2022-2023学年九年级上学期11月期中考试数学试题(含答案)

这是一份河南省郑州市第四初级中学2022-2023学年九年级上学期11月期中考试数学试题(含答案)，共6页。试卷主要包含了下列实数中，最小的是，已知等内容，欢迎下载使用。

一．选择题（共 10 小题，每小题 3 分，共 30 分）
1．下列实数中，最小的是（）
A．﹣πB．﹣（﹣1）C．﹣|﹣2|D．﹣3 2．如图是由 5 个相同的正方体搭成的立体图形，则它的主视图为（）
A．B．C．D．
3．2021 年 5 月 22 日，中国工程院院士袁隆平在长沙不幸逝世．这位“共和国勋章获得者” 的最大贡献是杂交水稻技术．2020 年我国水稻种植面积 4.5 亿亩，其中 50%左右是杂交水稻，则杂交水稻种植面积用科学记数法表示约为（ ）
A．4.5×108 亩B．2.25×108 亩C．4.5×109 亩D．2.25×109 亩
将抛物线 y＝5（x﹣2）2﹣3 向右移动 1 个单位，再向下移动 7 个单位，得到的抛物线的解析式为（ ）
A．y＝5（x+1）2B．y＝5（x+1）2﹣6
C．y＝5（x﹣3）2D．y＝5（x﹣3）2﹣10
如图，一条河的两岸互相平行，为了测量河的宽度 PT（PT 与河岸 PQ 垂直），测量得 P， Q 两点间距离为 m 米，∠PQT＝α，则河宽 PT 的长为（ ）
（第 5 题图）（第 8 题图）
A．msinαB．mcsαC．mtanαD．
若关于 x 的一元二次方程 ax2﹣4x+2＝0 有两个实数根，则 a 的取值范围是（）
A．a≤2B．a＜2C．a≤2 且 a≠0D．a＜2 且 a≠0
7．已知（﹣1，y1），B（﹣2，y2），（﹣4，y3）是抛物线 y＝2x2+8x﹣1 上的点，则下列结论正确的是（ ）
A．y1＜y2＜y3B．y3＜y2＜y1C．y3＜y1＜y2D．y2＜y1＜y3
在平面直角坐标系 xOy 中，二次函数 y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：
①abc＞0；②a﹣b+c＜0；③2a﹣b＝0；④b2＞4ac；⑤若 m 为任意实数，则 a+b≥ am2+bm．其中正确的个数是（）
个B．2 个C．3 个D．4 个
如图，在矩形 ABCD 中，对角线 AC、BD 相交于点 O，DF 垂直平分 OC，交 AC 于点 E， 交 BC 于点 F，连接 AF，若 AD＝3，则 AF 的长为（）
（第 9 题图）（第 10 题图）
A． B． C．2 D．3
如图，Rt△ABC 中，点 E 为 BC 的中点，点 P 沿 BC 从点 B 运动到点 C，设 B，P 两点间的距离为 x，PA﹣PE＝y，图 2 是点 P 运动时 y 随 x 变化的关系图象，则 BC 的长为（） A．6B．8C．10D．12
二．填空题（共 5 小题，每小题 3 分，共 15 分）
要使式子有意义，则实数 x 的取值范围是 ．
一个不透明的口袋中有四个完全相同的小球，其上分别标有数字 1，2，4，8．随机摸取一个小球后不放回，再随机摸取一个小球，则两次取出的小球上数字之积等于 8 的概率是 ．
如图，一次函数 y＝mx+n 的图象与二次函数 y＝ax2+bx+c 的图象交于 A（﹣1，p），B（4， q）两点，则关于 x 的不等式 mx+n＞ax2+bx+c 的解集是 ．
如图，菱形 ABCD 的边长为 2，∠ABC＝60°，对角线 AC 与 BD 交于点 O，E 为 OB 中点，
F 为 AD 中点，连接 EF，则 EF 的长为 ．
（第 13 题图）（第 14 题图）（第 15 题图）
如图，在矩形 ABCD 中，点 E 是 AB 的中点，点 F 为射线 AD 上的一个动点，△AEF 沿着EF 折叠得到△HEF，连接 AC，分别交 EF 和 EH 于点 N 和 M，已知 AB＝，BC＝2， 若△EMN 与△AEF 相似，则 AF 的长是 ．
三．解答题（共 8 小题，共 75 分）
16．（8 分）先化简，再求值：÷（x﹣），其中 x 为方程 x2﹣9x+18＝0 的实数根．
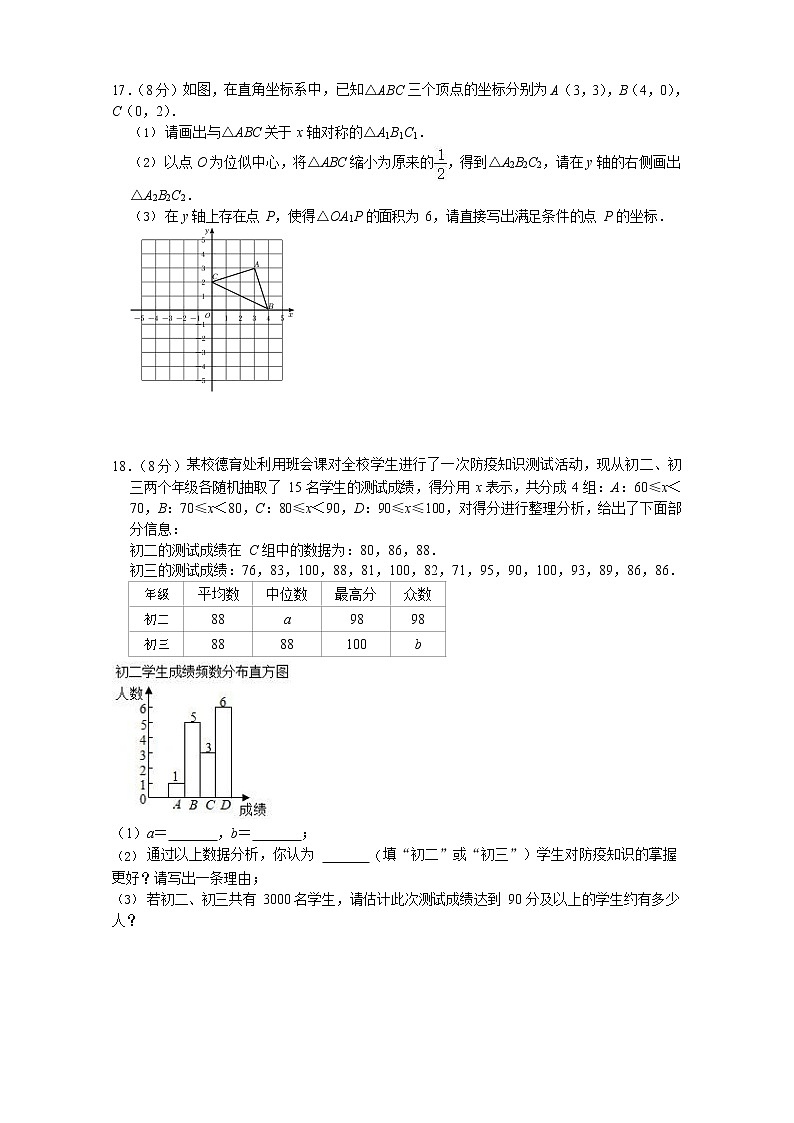
17．（8 分）如图，在直角坐标系中，已知△ABC 三个顶点的坐标分别为 A（3，3），B（4，0）， C（0，2）．
请画出与△ABC 关于 x 轴对称的△A1B1C1．
以点 O 为位似中心，将△ABC 缩小为原来的，得到△A2B2C2，请在 y 轴的右侧画出
△A2B2C2．
在 y 轴上存在点 P，使得△OA1P 的面积为 6，请直接写出满足条件的点 P 的坐标．
18．（8 分）某校德育处利用班会课对全校学生进行了一次防疫知识测试活动，现从初二、初三两个年级各随机抽取了 15 名学生的测试成绩，得分用 x 表示，共分成 4 组：A：60≤x＜ 70，B：70≤x＜80，C：80≤x＜90，D：90≤x≤100，对得分进行整理分析，给出了下面部分信息：
初二的测试成绩在 C 组中的数据为：80，86，88．
初三的测试成绩：76，83，100，88，81，100，82，71，95，90，100，93，89，86，86．
（1）a＝ ，b＝ ；
通过以上数据分析，你认为 （填“初二”或“初三”）学生对防疫知识的掌握更好？请写出一条理由；
若初二、初三共有 3000 名学生，请估计此次测试成绩达到 90 分及以上的学生约有多少人？
年级
平均数
中位数
最高分
众数
初二
88
a
98
98
初三
88
88
100
b
19．（9 分）如图，在平面直角坐标系 xOy 中，平行四边形 ABCD 的顶点 A、D 在 x 轴上，顶点 B 在 y 轴上，顶点 C 在反比例函数 y＝（n≠0）的图象上，直线 AB：y＝kx+b（k≠0）与反比例函数的图象交于点 M（﹣3，m），已知平行四边形 ABCD 的面积为 6．
求反比例函数的表达式及 m；
若 AD＝4，求直线 AB 的表达式．
20．（10 分）胜利黄河大桥犹如一架巨大的竖琴，凌驾于滔滔黄河之上，使黄河南北“天堑变通途”．已知主塔 AB 垂直于桥面 BC 于点 B，其中两条斜拉索 AD、AC 与桥面 BC 的夹角分别为 60°和 45°，两固定点 D、C 之间的距离约为 33m，求主塔 AB 的高度（结果保留整数，参考数据： ≈1.41， ≈1.73）
21．（10 分）冰墩墩是 2022 年北京冬季奥运会的吉祥物．某商家开始古样物“冰墩墩”纪念品的销售．每个纪念品进价 40 元．规定销售单价不低于 44 元．且不高于 52 元．销售期
间发现．当销售单价定为 44 元时．每天可出售 300 个．销售单价每上涨 1 元．每天销量减少
10 个．现商家决定提价销售．设每天销售量为 y 个．销售单价为 x 元．
求当每个纪念品的销售单价是多少元时．商家每天获利 2400 元；
将纪念品的销售单价定为多少元时．商家每天销售纪念品获得的利润 w 元最大？最大利润是多少元？
22．（11 分）如图，抛物线 y＝ax2+bx﹣3（a≠0）与 x 轴交于点 A（﹣1，0），点 B（3，0），与 y 轴交于点 C．
求抛物线的表达式；
在对称轴上找一点 Q，使△ACQ 的周长最小，求点 Q 的坐标；
（3）P 是第四象限内抛物线上的动点，求△BPC 面积 S 的最大值及此时 P 点的坐标．
23．（11 分）已知正方形 ABCD 的边长为 4，E、F 分别为边 DC、BC 上两点．
如图 1，若 BF＝CE，求证：AF＝BE．
如图 2，若 BF＝DE，作 EH⊥AF 于 H，连接 DH，求证：DH＝AB．
如图 3，若 DE＝CE，BF＝，点 G 在边 AB 上满足 EG＝AF，则 AG 长度为 .
（直接写出答案）