鲁教版 (五四制)八年级下册2 二次根式的性质学案设计

这是一份鲁教版 (五四制)八年级下册2 二次根式的性质学案设计，共3页。
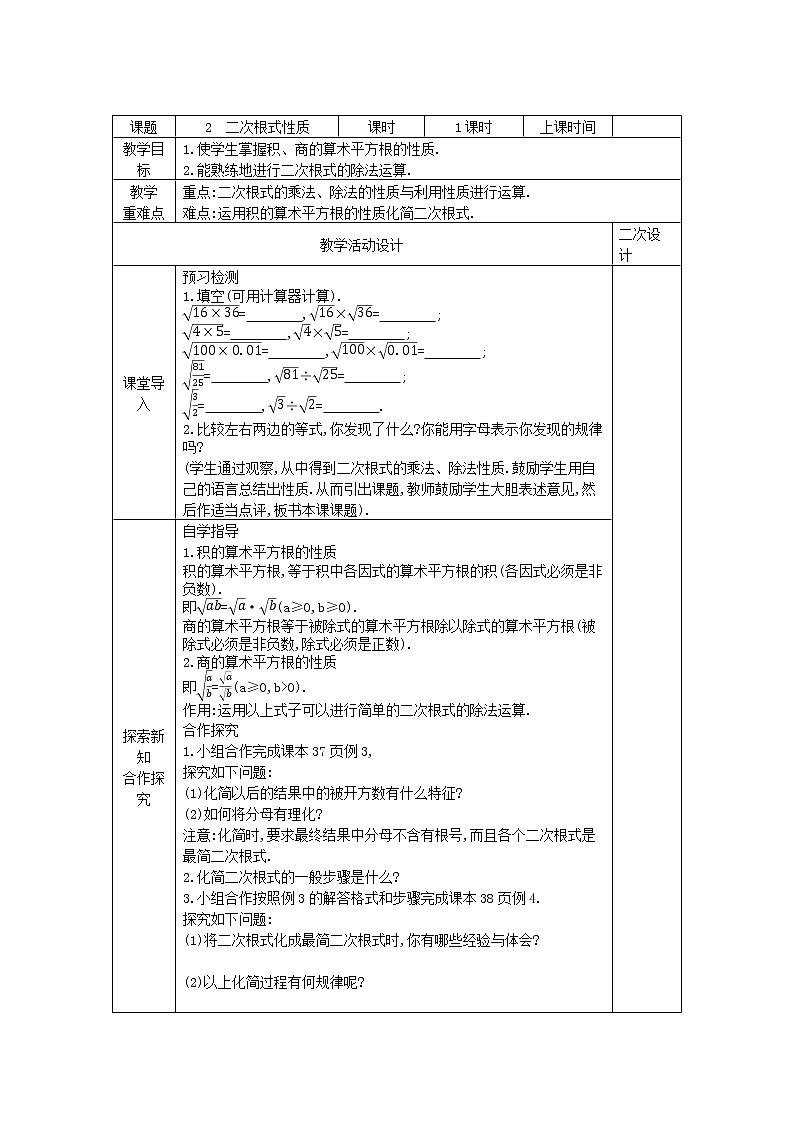
 课题2　二次根式性质课时1课时上课时间 教学目标1.使学生掌握积、商的算术平方根的性质.2.能熟练地进行二次根式的除法运算.教学重难点重点:二次根式的乘法、除法的性质与利用性质进行运算.难点:运用积的算术平方根的性质化简二次根式.教学活动设计二次设计课堂导入预习检测1.填空(可用计算器计算).=　　　　,×=　　　　; =　　　　,×=　　　　; =　　　　,×=　　　　; =　　　　,÷=　　　　; =　　　　,÷=　　　　. 2.比较左右两边的等式,你发现了什么?你能用字母表示你发现的规律吗?(学生通过观察,从中得到二次根式的乘法、除法性质.鼓励学生用自己的语言总结出性质.从而引出课题,教师鼓励学生大胆表述意见,然后作适当点评,板书本课课题). 探索新知合作探究自学指导1.积的算术平方根的性质积的算术平方根,等于积中各因式的算术平方根的积(各因式必须是非负数).即=·(a≥0,b≥0).商的算术平方根等于被除式的算术平方根除以除式的算术平方根(被除式必须是非负数,除式必须是正数).2.商的算术平方根的性质即=(a≥0,b>0).作用:运用以上式子可以进行简单的二次根式的除法运算.合作探究1.小组合作完成课本37页例3,探究如下问题:(1)化简以后的结果中的被开方数有什么特征?(2)如何将分母有理化?注意:化简时,要求最终结果中分母不含有根号,而且各个二次根式是最简二次根式.2.化简二次根式的一般步骤是什么?3.小组合作按照例3的解答格式和步骤完成课本38页例4.探究如下问题:(1)将二次根式化成最简二次根式时,你有哪些经验与体会? (2)以上化简过程有何规律呢?   续表探索新知合作探究[例题] 化简:(1);       (2);       (3);             (4).   教师指导1.易错点:(1)当二次根式的被开方数有待定系数时,必须检验被开方数是否满足非负.(2)化简二次根式时,要求最终结果中分母不含有根号,而且各个二次根式是最简二次根式.2.归纳小结:化简二次根式的一般步骤(1)准备:把被开方数化成乘除形式,并把分母化为完全平方形式;(2)化简:完全平方数(式)开平方后,分子移出根号作绝对值、分母移出根号作绝对值.3.方法规律:(1)利用式子=a(a≥0)可将根号内含字母的二次根式化简,结果也要化成最简二次根式.(2)·=(a≥0,b≥0),=(a≥0,b>0). 当堂训练1.若x<0,则-等于(　　)(A)x (B)2x (C)0 (D)-2x2.计算:=　　　　;=　　　　. 3.求代数式-×的值,其中a=3,b=2.        板书设计二次根式的性质1.=a(a≥0)           2.=·(a≥0,b≥0)    3.=(a≥0,b>0)教学反思在促进学生探索求知和有效学习方面还存在明显不足.新的教学理念要求教师在课堂教学中注意引导学生探究学习,经常为了完成教学任务而忽视这方面的引导.若能让学生在探究的基础上归纳出方法,学习的效果会提高很多,学习的能力也会不断提高.