




还剩52页未读,
继续阅读
人教版九年级下册第二十九章 投影与视图29.2 三视图课前预习ppt课件
展开
这是一份人教版九年级下册第二十九章 投影与视图29.2 三视图课前预习ppt课件,共60页。PPT课件主要包含了三视图,素养目标,三视图的定义及关系,从前面看,从左面看,从上面看,从正面看,画物体的三视图,圆柱1,主视图等内容,欢迎下载使用。
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中”你能说明是什么原因吗?
1. 能从投影的角度理解视图的概念,明确视图与投影的关系.
2.能识别物体的三视图,会画简单几何体的三视图.
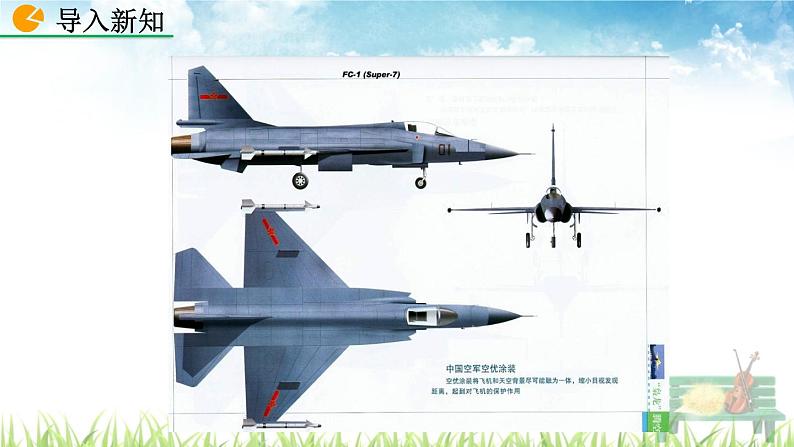
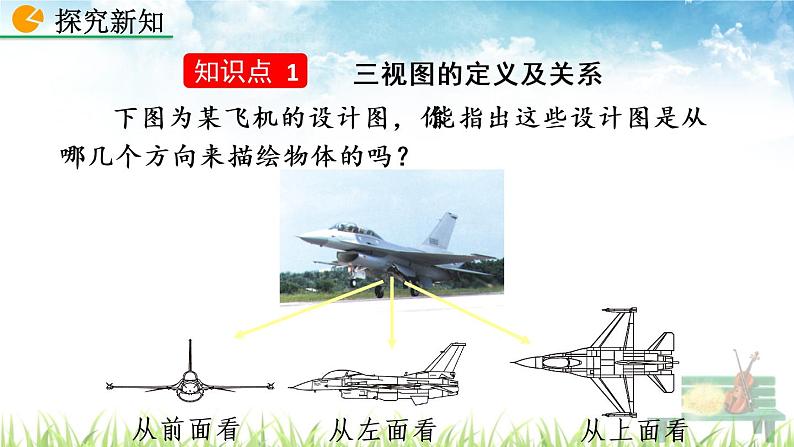
下图为某飞机的设计图,你能指出这些设计图是从哪几个方向来描绘物体的吗?
请你从前、后、左、右、上、下六个方向观察同一本字典,画出得到的正投影,你有什么发现?
1. 前面和后面正投影的形状、大小一致;
2. 上面和下面正投影的形状、大小一致;
3. 左面和右面正投影的形状、大小一致;
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.视图也可以看作物体在某一方向光线下的正投影,对于同一个物体,如果从不同方向观察,所得到的视图可能不同.
1. 三个投影面 我们用三个互相垂直的平面(例如:墙角处的三面墙面壁)作为投影面,其中正对着我们的平面叫正面,下方的平面叫水平面,右边的平面叫做侧面.
你能说出这三个视图分别是从哪三个方向观察这本书得到的吗?
这些图形的投影面分别在什么位置?
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
三视图是主视图、俯视图、左视图的统称.它是从三个方向分别表示物体形状的一种常用视图.
对一个物体在三个投影面内进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.
例1 画出图中基本几何体的三视图:
已知简单几何体画三视图
正三棱柱 (2)
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
1. 画出半球和圆锥的三视图.
例2 画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
2.(2018•菏泽)如图是两个等直径圆柱构成的“T”形管道,其左视图是( )A. B. C. D.
例3 画出该几何体的三视图.
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
解:下图是组合体的三视图.
3.画出图中简单组合体的三视图:
1.(2018•广安)下列图形中,主视图为图①的是( )
A. B. C. D.
2.(2019•孝感)下列立体图形中,左视图是圆的是( )A. B. C. D.
1.(2018•眉山)下列立体图形中,主视图是三角形的是( ) A. B. C. D.
2.一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是( ) A.球 B.正三棱锥 C.正方体 D.圆柱
3.将矩形硬纸板绕它的一条边旋转180°所形成的几何体的主视图和俯视图不可能是( ) A.矩形,矩形 B.半圆、矩形 C.圆、矩形 D.矩形、半圆
4.下图中①表示的是组合在一起的模块,那么这个模块的俯视图是( )
A.② B.③ C.④ D.⑤
① ② ③ ④ ⑤
5.找出对应的三视图.
画出图中的几何体的三视图.
图是一根钢管的直观图,画出它的三视图.
前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论怎样由三视图想象出立体图形(实物)?
下面是哪个几何体的三视图?
主视图 左视图 俯视图
2. 会根据复杂的三视图判断实物原型,能做出原事物的几何图形.
1. 会根据物体的三视图描述出基本几何体的形状,并且会做出原实物的几何图形 .
3. 通过由三视图确定物体原型的过程,培养学生的空间想象能力.
例1 如图,分别根据三视图(1) (2)说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
根据三视图描述较简单物体的形状
解:(1)从三个方向看立体图形,视图都是矩形,可以想象出:整体是 ,如图1所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形; 从上面看,视图是圆;可以想象出:整体是 ,如图2所示.
1.由三视图想象实物现状:
例2 根据物体的三视图描述物体的形状.
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
根据三视图描述较复杂物体的形状
解:物体是正五棱柱形状的,如图所示.
【方法总结】由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
2.根据下列物体的三视图,填出几何体的名称:(1) 如图①所示的几何体是__________;(2) 如图②所示的几何体是_________.
例3 请根据下面提供的三视图,画出几何图形.
根据三视图画出几何体的图形
3.请根据下面提供的三视图,画出几何图形.
4.请根据下面提供的三视图,画出几何图形.
1.(2018•襄阳)一个几何体的三视图如图所示,则这个几何体是( )A. B. C. D.
2.(2018•金华)一个几何体的三视图如图所示,该几何体是( ) A.直三棱柱 B.长方体 C.圆锥 D.立方体
1. 下列三视图所对应的实物图是 ( )
2. (2018•泰安)如图是下列哪个几何体的主视图与俯视图( )
A. B. C. D.
3. (1) 一个几何体的主视图和左视图如图所示,请补画这个几何体的俯视图.
(2) 一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
在一仓库里堆放着若干相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如下图所示,则这堆正方体货箱共有 箱.
根据三视图画出实物图形
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
由三视图确定几何体的面积或体积
如图,根据右边图中椅子的三视图,工人就能制造出符合设计要求的椅子.
你想知道他们是如何做到的吗?我们一起继续学习视图!
1. 能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.
2. 由三视图想象出立体图形后能进行简单的面积或体积的计算.
分析:1. 应先由三视图想象出 ; 2. 画出物体的 .
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
利用三视图求物体的表面积
解:由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
由展开图可知,制作一个密封罐所需钢板的面积为
由三视图求立体图形的面积的方法: (1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高. (2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分. (3) 最后根据已知数据,求出展开图的面积.
1. 如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.
解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为
例2 一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
解:长方体,其体积为10×12×15=1800(cm3).
利用三视图求物体的体积
分析:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.
2. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的体积为 .
主视图 左视图 俯视图
(2018•东营)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
解析:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,所以圆锥的母线长 ,所以这个圆锥的侧面积是π×4×5=20π.
1. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 ( )
A. 6 B. 8 C. 12 D. 24
2. 如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
3. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
4.如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积,然后相加即可.
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
体积为25×30×40+102×32π=(30000+3200π)(cm3).
表面积为20π×32+(30×40+25×40+25×30)×2=(5900+640π)(cm2),
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图. (1) 请写出构成这个几何体的正方体的个数为 ; (2) 计算这个几何体的表面积为 .
某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
1. 三种图形的转化:
2. 由三视图求立体图形的体积 (或面积) 的方法:(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中”你能说明是什么原因吗?
1. 能从投影的角度理解视图的概念,明确视图与投影的关系.
2.能识别物体的三视图,会画简单几何体的三视图.
下图为某飞机的设计图,你能指出这些设计图是从哪几个方向来描绘物体的吗?
请你从前、后、左、右、上、下六个方向观察同一本字典,画出得到的正投影,你有什么发现?
1. 前面和后面正投影的形状、大小一致;
2. 上面和下面正投影的形状、大小一致;
3. 左面和右面正投影的形状、大小一致;
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.视图也可以看作物体在某一方向光线下的正投影,对于同一个物体,如果从不同方向观察,所得到的视图可能不同.
1. 三个投影面 我们用三个互相垂直的平面(例如:墙角处的三面墙面壁)作为投影面,其中正对着我们的平面叫正面,下方的平面叫水平面,右边的平面叫做侧面.
你能说出这三个视图分别是从哪三个方向观察这本书得到的吗?
这些图形的投影面分别在什么位置?
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
三视图是主视图、俯视图、左视图的统称.它是从三个方向分别表示物体形状的一种常用视图.
对一个物体在三个投影面内进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.
例1 画出图中基本几何体的三视图:
已知简单几何体画三视图
正三棱柱 (2)
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注意与主视图“长对正”;
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
1. 画出半球和圆锥的三视图.
例2 画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
2.(2018•菏泽)如图是两个等直径圆柱构成的“T”形管道,其左视图是( )A. B. C. D.
例3 画出该几何体的三视图.
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
解:下图是组合体的三视图.
3.画出图中简单组合体的三视图:
1.(2018•广安)下列图形中,主视图为图①的是( )
A. B. C. D.
2.(2019•孝感)下列立体图形中,左视图是圆的是( )A. B. C. D.
1.(2018•眉山)下列立体图形中,主视图是三角形的是( ) A. B. C. D.
2.一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是( ) A.球 B.正三棱锥 C.正方体 D.圆柱
3.将矩形硬纸板绕它的一条边旋转180°所形成的几何体的主视图和俯视图不可能是( ) A.矩形,矩形 B.半圆、矩形 C.圆、矩形 D.矩形、半圆
4.下图中①表示的是组合在一起的模块,那么这个模块的俯视图是( )
A.② B.③ C.④ D.⑤
① ② ③ ④ ⑤
5.找出对应的三视图.
画出图中的几何体的三视图.
图是一根钢管的直观图,画出它的三视图.
前面我们讨论了由立体图形(实物)画出三视图,下面我们讨论怎样由三视图想象出立体图形(实物)?
下面是哪个几何体的三视图?
主视图 左视图 俯视图
2. 会根据复杂的三视图判断实物原型,能做出原事物的几何图形.
1. 会根据物体的三视图描述出基本几何体的形状,并且会做出原实物的几何图形 .
3. 通过由三视图确定物体原型的过程,培养学生的空间想象能力.
例1 如图,分别根据三视图(1) (2)说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
根据三视图描述较简单物体的形状
解:(1)从三个方向看立体图形,视图都是矩形,可以想象出:整体是 ,如图1所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形; 从上面看,视图是圆;可以想象出:整体是 ,如图2所示.
1.由三视图想象实物现状:
例2 根据物体的三视图描述物体的形状.
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
根据三视图描述较复杂物体的形状
解:物体是正五棱柱形状的,如图所示.
【方法总结】由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
2.根据下列物体的三视图,填出几何体的名称:(1) 如图①所示的几何体是__________;(2) 如图②所示的几何体是_________.
例3 请根据下面提供的三视图,画出几何图形.
根据三视图画出几何体的图形
3.请根据下面提供的三视图,画出几何图形.
4.请根据下面提供的三视图,画出几何图形.
1.(2018•襄阳)一个几何体的三视图如图所示,则这个几何体是( )A. B. C. D.
2.(2018•金华)一个几何体的三视图如图所示,该几何体是( ) A.直三棱柱 B.长方体 C.圆锥 D.立方体
1. 下列三视图所对应的实物图是 ( )
2. (2018•泰安)如图是下列哪个几何体的主视图与俯视图( )
A. B. C. D.
3. (1) 一个几何体的主视图和左视图如图所示,请补画这个几何体的俯视图.
(2) 一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
在一仓库里堆放着若干相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如下图所示,则这堆正方体货箱共有 箱.
根据三视图画出实物图形
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
由三视图确定几何体的面积或体积
如图,根据右边图中椅子的三视图,工人就能制造出符合设计要求的椅子.
你想知道他们是如何做到的吗?我们一起继续学习视图!
1. 能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.
2. 由三视图想象出立体图形后能进行简单的面积或体积的计算.
分析:1. 应先由三视图想象出 ; 2. 画出物体的 .
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
利用三视图求物体的表面积
解:由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
由展开图可知,制作一个密封罐所需钢板的面积为
由三视图求立体图形的面积的方法: (1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高. (2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分. (3) 最后根据已知数据,求出展开图的面积.
1. 如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.
解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为
例2 一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
解:长方体,其体积为10×12×15=1800(cm3).
利用三视图求物体的体积
分析:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.
2. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的体积为 .
主视图 左视图 俯视图
(2018•东营)已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
解析:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,所以圆锥的母线长 ,所以这个圆锥的侧面积是π×4×5=20π.
1. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 ( )
A. 6 B. 8 C. 12 D. 24
2. 如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
3. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
4.如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积,然后相加即可.
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
体积为25×30×40+102×32π=(30000+3200π)(cm3).
表面积为20π×32+(30×40+25×40+25×30)×2=(5900+640π)(cm2),
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图. (1) 请写出构成这个几何体的正方体的个数为 ; (2) 计算这个几何体的表面积为 .
某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
1. 三种图形的转化:
2. 由三视图求立体图形的体积 (或面积) 的方法:(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).













