2023年九年级数学中考专题训练：二次函数综合压轴题（特殊三角形问题）及答案

这是一份2023年九年级数学中考专题训练：二次函数综合压轴题（特殊三角形问题）及答案，共13页。试卷主要包含了如图等内容，欢迎下载使用。
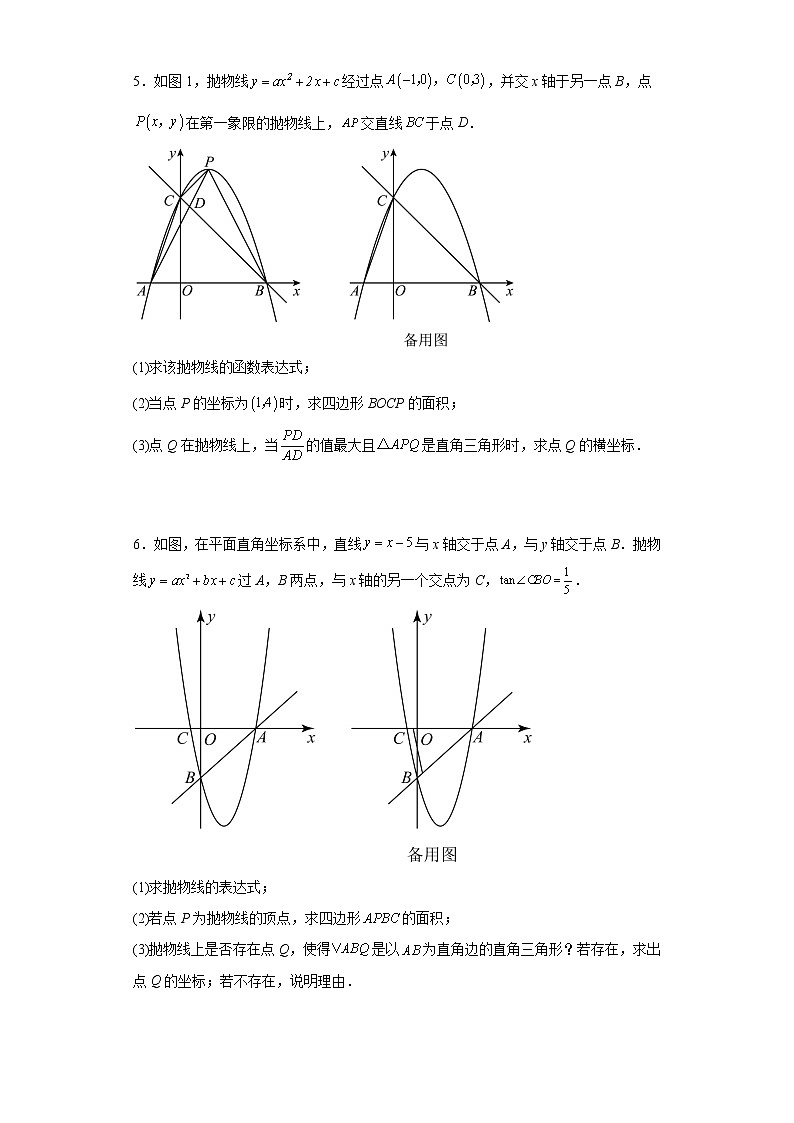
2023年九年级数学中考专题训练：二次函数综合压轴题（特殊三角形问题） 1．如图，已知二次函数的图象交x轴于点，，交y轴于点C．(1)求这个二次函数的表达式；(2)直线分别交直线和抛物线于点M，N，当是等腰三角形时，直接写出m的值．   2．如图，直线交x轴于点B、y轴于点C，抛物线经过点B，点C，且过，连接，点P是第一象限内抛物线上的一个动点．(1)求此抛物线的表达式；(2)动点P运动到什么位置时，的面积最大？若存在，请求出符合条件的P点的坐标；若不存在，请说明理由；(3)过点P作轴，垂足为点M，交于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点P的坐标，若不存在，请说明理由；  3．如图，直线分别与轴、轴交于点与点，函数的图像经过点．点是抛物线上的一个动点，过点作轴的垂线，过点作于点(1)求该二次函数的解析式；(2)连接，当为直角三角形时，求的长；(3)将绕点逆时针旋转，得到，当点的对应点落在坐标轴上时，请求出点的坐标．  4．如图，设拋物线与轴交于A、两点，与轴交于点．点为该抛物线第四象限上的一点，过作轴交于点．(1)求直线的解析式；(2)求线段的最大值；(3)当面积最大时，求点的坐标；(4)当为等腰三角形时，直接写出点的坐标． 5．如图1，抛物线经过点，并交x轴于另一点B，点在第一象限的抛物线上，交直线于点D．(1)求该抛物线的函数表达式；(2)当点Р的坐标为时，求四边形BOCP的面积；(3)点Q在抛物线上，当的值最大且是直角三角形时，求点Q的横坐标．  6．如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B．抛物线过A，B两点，与x轴的另一个交点为C，．(1)求抛物线的表达式；(2)若点P为抛物线的顶点，求四边形的面积；(3)抛物线上是否存在点Q，使得是以为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，说明理由．  7．如图．抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为．(1)请直接写出A，B两点的坐标及直线l的函数表达式；(2)若点P是抛物线上的点，点P的横坐标为，过点P作轴，垂足为M．与直线l交于点N，当点N是线段的三等分点时，求点P的坐标；(3)若点Q是对称轴上的点，且为直角三角形，求点Q的坐标．  8．如图，抛物线与x轴相交于A、B两点，与y轴相交于点C，且点B与点C的坐标分别为，，点M是抛物线的顶点．(1)求二次函数的关系式；(2)点P为线段MB上一个动点，过点P作轴于点D．若，的面积为S，试判断S有最大值或最小值？并说明理由；(3)在MB上是否存在点P，使为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．   9．如图，抛物线y＝ax2+bx+6（a≠0）与x轴交于点A（2，0）和点B（﹣6，0），与y轴交于点C．(1)求抛物线的解析式；(2)在抛物线上是否存在一点P，使△PAB的面积与△ABC的面积相等，若存在，求出点P的坐标；若不存在，请说明理由．(3)设抛物线的对称轴与x轴交于点M，在对称轴上存在点Q，使△CMQ是以MC为腰的等腰三角形，请直接写出所有符合条件的点Q的坐标．  10．如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在抛物对称轴上找一点D，使∠DCB＝∠CBD，求点D的坐标；(3)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．   11．如图，已知抛物线经过点A(-1，0)，B(4，0)，C(0，2)三点，点D与点C关于x轴对称，点P是线段AB上的一个动点，设点P的坐标为(m，0)，过点P作x轴的垂线l交抛物线于点Q，交直线BD于点M．(1)求该抛物线所表示的二次函数的表达式；(2)在点P运动过程中，是否存在点Q，使得△BQM是直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；(3)连接AC，将△AOC绕平面内某点H顺时针旋转90°，得到，点A、O、C的对应点分别是点、、、若的两个顶点恰好落在抛物线上，那么我们就称这样的点为“和谐点”，请直接写出“和谐点”的个数和点的横坐标．  12．如图，二次函数y＝ax2＋bx＋c(a≠0)的图象交x轴于A、B两点，交y轴于点D，点B的坐标为(3，0)，顶点C的坐标为(1，4)．(1)求二次函数的解析式；(2)点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；(3)在抛物线上是否存在点Q，且点Q在第一象限，使△BDQ中BD边上的高为？若存在，直接写出点Q的坐标；若不存在，请说明理由． 13．如图①，已知抛物线L：y＝x2+bx+c的图象经过点A（0，3），B（1，0），过点A作ACx轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点．(1)求抛物线的关系式；(2)若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出P点坐标；(3)将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE内（包括△OAE的边界），求h的取值范围；(4)如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．  14．如图，在平面直角坐标系中，已知抛物线与x轴交于点、，与y轴交于点C，顶点为D．(1)求抛物线的表达式和点D的坐标；(2)点E是第一象限内抛物线的一个动点，其横坐标为m，直线交y轴于点F．①用m的代数式表示直线的截距；②在的面积与的面积相等的条件下探究：在y轴右侧存在这样一条直线，满足：以该直线上的任意一点及点C、F三点为顶点的三角形的面积都等于面积，试用规范、准确的数学语言表达符合条件的直线．  15．如图．在平面直角坐标系中，已如抛物线与x轴交于两点，与y轴交于点．(1)求抛物线的解析式；(2)在抛物线上是否存在点P，使得是以点A为直角顶点的直角三角形？若存在，求出符合条件的点P的坐标：若不存在，请说明理由；(3)点G为抛物线上的一动点，过点G作垂直于y轴于点E，交直线于点D，过点D作x轴的垂线垂足为点F，连接，当线段的长度最短时，求出点G的坐标．  16．已知抛物线与x轴交于A，B两点，点A在点B的左边，与y轴交于点C（0，3），且AB=5；(1)求二次函数的解析式；(2)点N是线段OB上（端点除外）的一个动点，过点N作NM∥y轴，交BC于点P，交抛物线于点M，且PN∶PM=1∶2．①求此时的N点坐标；②试探究，在抛物线的对称轴上是否存在一点Q，使得△CNQ为直角三角形，若存在，请求Q点坐标；不存在，请说明理由．  17．抛物线与x轴交于A、B两点（点A在点B的左侧），且，，与y轴交于点C．连接BC，以BC为边，点O为中心作菱形BDEC．点P是x轴上的一个动点，设点P的坐标为，过点P作x轴的垂线交抛物线于点Q，交BD于点M．(1)求该抛物线对应的函数表达式；(2)x轴上是否存在一点P，使为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由；(3)当点P在线段OB上运动时，试探究：当m为何值时，四边形CQMD是平行四边形？请说明理由．  18．已知二次函数的图象与轴交于和，与轴交于点．(1)求该二次函数的表达式．(2)如图，连接，动点以每秒个单位长度的速度由向运动，同时动点以每秒个单位长度的速度由向运动，连接，当点到达点的位置时，、同时停止运动，设运动时间为秒．当为直角三角形时，求的值．(3)如图，在抛物线对称轴上是否存在一点，使得点到轴的距离与到直线的距离相等，若存在，求出点的坐标；若不存在，请说明理由．
参考答案：1．(1)；(2)的值为，，1，2 2．(1)(2)(3)或 3．(1)(2)或(3)或 4．(1)(2)(3)(4)或或 5．(1)(2)(3)或或或 6．(1)；(2)；(3)点Q的坐标为或． 7．(1)，，直线l的解析式为；(2)P的坐标为或；(3)点Q的坐标为或或或． 8．(1)(2)存在最大值，最大值为(3)或 9．(1)y＝(2)存在，点P的坐标为：（﹣2+，﹣6）或（﹣2﹣，﹣6）或（﹣4，6）(3)点Q的坐标为（﹣2，2）或（﹣2，﹣2）或（﹣2，12） 10．(1)(2)(3) 11．(1)(2)存在，Q(3，2)或Q(-1，0)(3)两个“和谐点”，的横坐标是1或 12．(1)y＝﹣x2＋2x＋3(2)(3)存在，(1，4)或(2，3) 13．(1)抛物线的解析式为：y＝x2﹣4x+3(2)P点坐标为（，）(3)h的取值范围为3≤h≤4(4)存在，点P的坐标是（，）或（，）或（，）或（，）14．(1)，点D的坐标为(2)①直线的截距是；②符合条件的直线应该是经过点E且垂直于x轴的直线，为直线和直线15．(1)(2)存在，P（-5，-20）(3)G或16．(1)(2)①②存在一点Q，使得△CNQ为直角三角形，点Q的坐标为或或或． 17．(1)(2)存在，点P的坐标为（0，0）或或或（－4，0）(3)当m＝2时，四边形CQMD是平行四边形，理由见解析 18．(1)(2)或2(3)存在；或