
2023年九年级数学中考专题训练:二次函数综合压轴题(线段周长问题)及答案
展开2023年九年级数学中考专题训练:二次函数综合压轴题(线段周长问题)
1.如图,抛物线与x轴交于两点,A点坐标为,C点坐标为,与y轴交于点.点P是抛物线上的一动点,且点P在直线的下方,过点P作x轴的垂线,交直线于点E,垂足为D.
(1)求抛物线的表达式;
(2)当最大时,求点P的坐标;
(3)在(2)的条件下(即最大时)问在直线上是否存在点Q,使为直角三角形?若存在,求出符合条件的Q点的坐标,若不存在,请说明理由.
2.如图,在平面直角坐标系中,抛物线与直线交于,两点,点在轴上,点的横坐标为.
(1)点坐标为_________,点坐标为_________.
(2)求此抛物线所对应的函数解析式.
(3)点是抛物线上一点,点与点不重合,设点的横坐标为,过点作轴,交直线于点,设的长为.
①若点在直线的上方,求关于的函数解析式;
②若点在轴的上方,当随的增大而增大时,直接写出的取值范围.
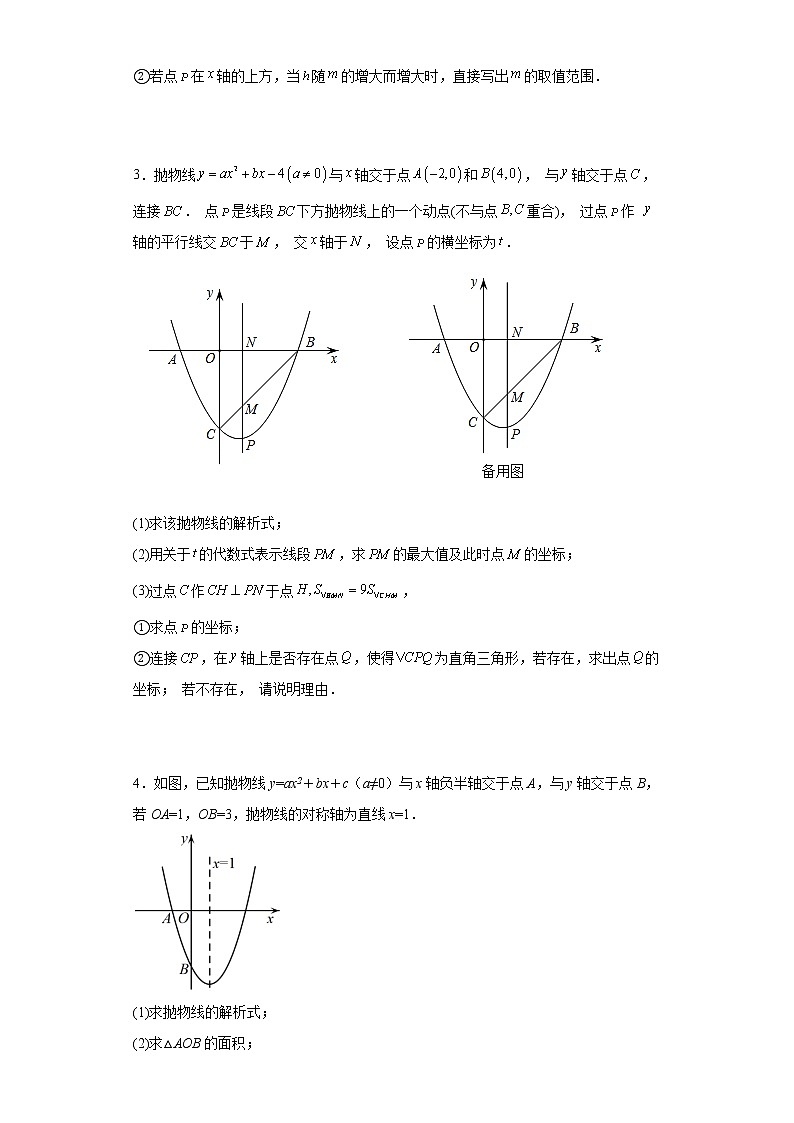
3.抛物线与轴交于点和, 与轴交于点, 连接. 点是线段下方抛物线上的一个动点(不与点重合), 过点作 轴的平行线交于, 交轴于, 设点的横坐标为.
(1)求该拋物线的解析式;
(2)用关于的代数式表示线段,求的最大值及此时点的坐标;
(3)过点作于点,
①求点的坐标;
②连接,在轴上是否存在点,使得为直角三角形,若存在,求出点的坐标; 若不存在, 请说明理由.
4.如图,已知抛物线y=ax2+bx+c(a≠0)与x轴负半轴交于点A,与y轴交于点B,若OA=1,OB=3,抛物线的对称轴为直线x=1.
(1)求抛物线的解析式;
(2)求△AOB的面积;
(3)若抛物线上另有一点P满足S△PAO=S△AOB,请求出点P的坐标;
(4)在抛物线的对称轴上,是否存在点P,使它到点A的距离与到点B的距离之和最小?如果存在,请求出点P的坐标;如果不存在,请说明理由.
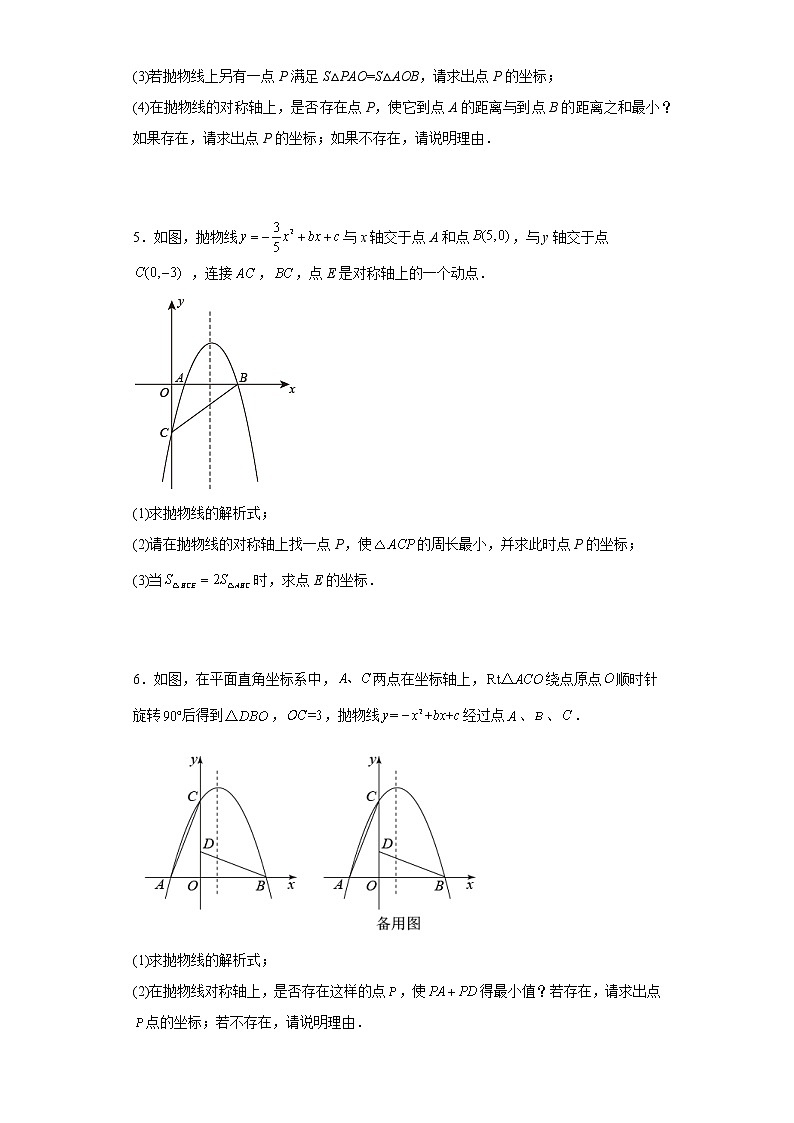
5.如图,抛物线与x轴交于点A和点,与y轴交于点 ,连接,,点E是对称轴上的一个动点.
(1)求抛物线的解析式;
(2)请在抛物线的对称轴上找一点P,使的周长最小,并求此时点P的坐标;
(3)当时,求点E的坐标.
6.如图,在平面直角坐标系中,两点在坐标轴上,绕点原点顺时针旋转后得到,,抛物线经过点、、.
(1)求抛物线的解析式;
(2)在抛物线对称轴上,是否存在这样的点,使得最小值?若存在,请求出点点的坐标;若不存在,请说明理由.
(3)在抛物线上有一点,使得是以为直角边的直角三角形,请直接写出点的坐标.
7.如图,在平面直角坐标系中,O为坐标原点,抛物线与x轴的一个交点为A(3,0),与y轴的交点为B(0,﹣3).点P为该抛物线上的任意一点,过点P分别向x轴、y轴作垂线,垂足分别为M、N.设点P的横坐标为m.
(1)求该抛物线的解析式;
(2)当点A在四边形OMPN的边上时,用含m的代数式表示该四边形的周长;
(3)当该抛物线的顶点和点B到PN所在直线的距离相等时,求m的值;
(4)当抛物线在矩形PNOM内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.
8.如图,抛物线交x轴于点A(1,0),交y轴交于点B,对称轴是直线x=2.
(1)求抛物线的解析式;
(2)若在抛物线上存在一点D,使△ACD的面积为8,请求出点D的坐标.
(3)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
9.已知抛物线交轴于、两点,在的左边,交轴于点.
(1)求抛物线顶点的坐标;
(2)如图1,若,在抛物线上且在直线上方,于,求的最大值;
(3)如图2,点()在抛物线上,过作直线交抛物线于第四象限另一点,点在轴上,以、、为顶角的三角形与相似,求点的坐标.
10.如图,抛物线与x轴交于点,点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在对称轴上找一点Q,使的周长最小,求点Q的坐标;
(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.
11.综合与探究:
如图,在平面直角坐标系中,二次函数的图象经过点,点.
(1)求此二次函数的解析式;
(2)当时,求二次函数的最大值和最小值;
(3)点P为此函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为.已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.求m的取值范围;
12.如图1,在平面直角坐标系中.抛物线与x轴交于和,与y轴交于点C,连接.
(1)求该抛物线的解析式;
(2)如图2,点M为直线上方的抛物线上任意一点,过点M作y轴的平行线,交于点N,过点M作x轴的平行线,交直线于点Q,求周长的最大值;
(3)点P为抛物线上的一动点,且,请直接写出满足条件的点P的坐标.
13.如图1,抛物线经过,,点B在x轴上,且,过点B作轴交抛物线于点D,点E,F分别是线段CO,BC上的动点,且,连接EF.
(1)求抛物线的表达式及点D的坐标;
(2)当是直角三角形时,求点F的坐标;
(3)如图2,连接AE,AF,直接写出的最小值为:______.
14.抛物线与轴交于A,B(3,0)两点,与y轴交于点C,顶点为D.
(1)求m的值及顶点D的坐标;
(2)如图1,若点E是抛物线上对称轴右侧一点,设点E到直线AC的距离为,到抛物线的对称轴的距离为,当时,请求出点E的坐标.
(3)如图2,直线交抛物线于点M,N,连接AM,AN分别交y轴的正半轴和负半轴于点P,Q,试探究线段OP,OQ之间的数量关系.
15.如图,抛物线L:与x轴交于点,两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为.
(1)求抛物线L和直线l的解析式;
(2)当点P在L上时,求m的值;
(3)过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.
①当线段,求m的值;
②若P,M,N三点不重合,当其中两点关于第三点对称时,直接写出m的值.
16.如图1,直线y=2x+2交x轴于点A,交y轴于点C,过A、C两点的抛物线与x轴的另一交点为B.
(1)求该抛物线的函数表达式;
(2)如图2,点D是抛物线在第一象限内的一点,连接OD,将线段OD绕O逆时针旋转90°得到线段OM,过点M作MN∥x轴交直线AC于点N.求线段MN的最大值及此时点D的坐标;
(3)在(2)的条件下,若点E是点A关于y轴的对称点,连接DE,试探究在抛物线上是否存在点P,使得∠PED=45°?若存在,求出点P的坐标;若不存在,请说明理由.
17.如图,在平面直角坐标系中,二次函数的图像交x轴于A、B两点,与y轴交于点C,OB=3OA=3,点P是抛物线上一动点.
(1)求抛物线的解析式及点C坐标;
(2)如图1,若点P在第一象限内,过点P作x轴的平行线,交直线BC于点E,求线段PE的最大值及此时点P的坐标;
(3)如图2,过点P作x轴的垂线交x轴于点Q,交直线BC于点M,在y轴上是否存在点G,使得以M,P,C,G为顶点的四边形为菱形?若存在,请直接写出所有满足条件的点G坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,二次函数的图象交y轴于点D,直线AB与之相交,且是抛物线的顶点.
(1)b=______,c=______;
(2)如图1,点P是第四象限抛物线上一点,且满足,抛物线交x轴于点C,连接PC.
①求直线PB的解析式;
②求PC的长;
(3)如图2,点Q是抛物线第三象限上一点(不与点B、D重合),连接BQ,以BQ为边作正方形BEFQ,当顶点E或F恰好落在抛物线对称轴上时,直接写出对应的Q点的坐标.
参考答案:
1.(1)
(2)
(3)存在, Q点的坐标为或
2.(1),
(2)
(3);或
3.(1)
(2),
(3)①;②存在点或
4.(1)y=x2﹣2x﹣3
(2)
(3),,
(4)(1,﹣2)
5.(1)抛物线的解析式为
(2)找点P见解析,
(3)点E的坐标为或
6.(1)
(2)存在,
(3)或或
7.(1)
(2)
(3)m=1+或m=1-
(4)m<-1或0<m<2
8.(1)
(2)D(5,8)或(﹣1,8)
(3)存在,(2,1)
9.(1)(,)
(2)
(3)(2,0)或(-5,0)或或
10.(1)
(2)(1,-2)
(3)(-1,0)或(,-2)或(,2)
11.(1)
(2)最小值为-2,最大值为
(3)
12.(1)
(2)
(3)或
13.(1),点D(-3,-5);
(2)或
(3)
14.(1),
(2)
(3)
15.(1),y=x-3;
(2)m=1或3;
(3)m的值为﹣1、0、、1、2、3.
16.(1)
(2)最大值为3;
(3)存在,,
17.(1)抛物线的解析式为y=−x2+2x+3;C(0,3);
(2)PE最大值为,点P的坐标为(,);
(3)点G的坐标为(0,1)或(0,3+1)或(0,1-3).
18.(1)-1;4
(2)①y=−x−1;②
(3)(,)或(,−3)
专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案解析版docx、专题26二次函数与线段周长压轴问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共91页, 欢迎下载使用。
中考数学压轴题满分突破训练 专题08 二次函数-线段之差最值问题: 这是一份中考数学压轴题满分突破训练 专题08 二次函数-线段之差最值问题,文件包含专题08二次函数-线段之差最值问题解析版docx、专题08二次函数-线段之差最值问题原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
中考数学压轴题满分突破训练 专题06 二次函数-周长最大值问题: 这是一份中考数学压轴题满分突破训练 专题06 二次函数-周长最大值问题,文件包含专题06二次函数-周长最大值问题解析版docx、专题06二次函数-周长最大值问题原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












