陕西省西安市周至县2021-2022学年九年级上学期期中考试数学试题（有答案）

这是一份陕西省西安市周至县2021-2022学年九年级上学期期中考试数学试题（有答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
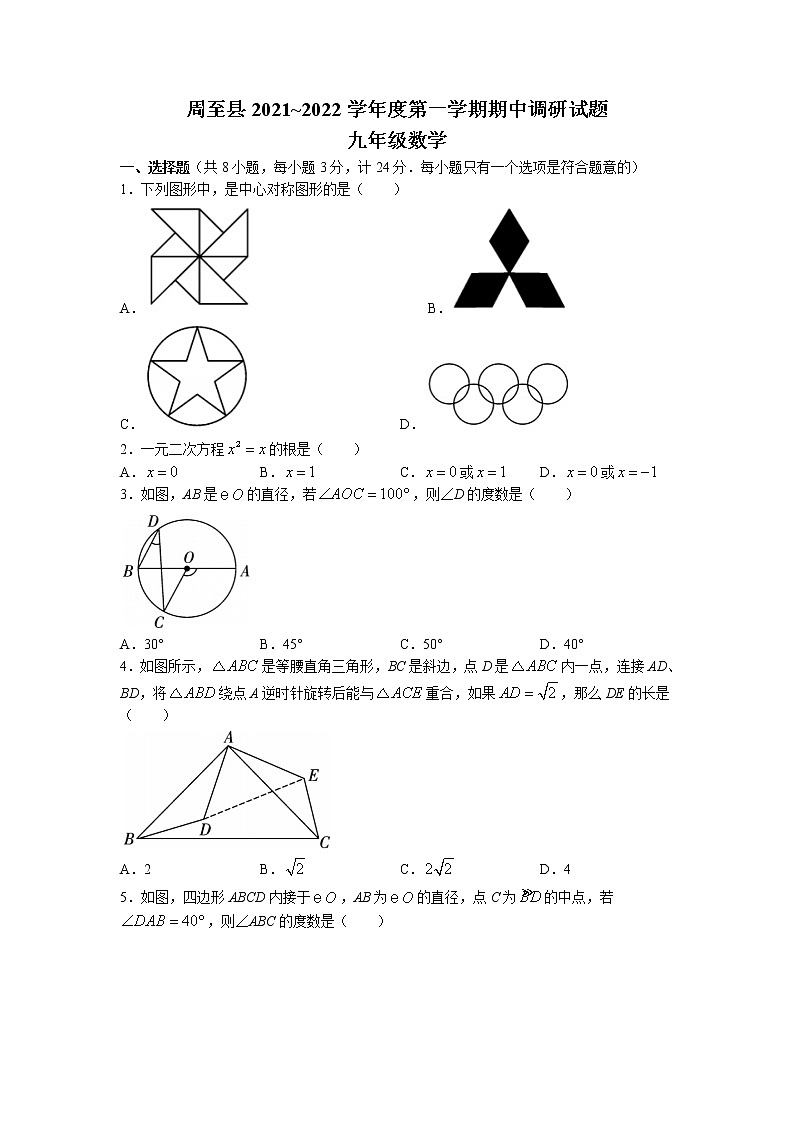
周至县2021~2022学年度第一学期期中调研试题九年级数学一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．下列图形中，是中心对称图形的是（    ）A．      B．C．      D．2．一元二次方程的根是（    ）A．   B．   C．或  D．或3．如图，AB是的直径，若，则∠D的度数是（    ）A．30°    B．45°    C．50°    D．40°4．如图所示，是等腰直角三角形，BC是斜边，点D是内一点，连接AD、BD，将绕点A逆时针旋转后能与重合，如果，那么DE的长是（    ）A．2    B．    C．   D．45．如图，四边形ABCD内接于，AB为的直径，点C为的中点，若，则∠ABC的度数是（    ）A．80°    B．70°    C．50°    D．40°6．二次函数的图象与x轴只有一个交点，则m的值是（    ）A．8    B．16    C．－8    D．－167．某市严格落实国家节水政策，2018年用水总量为6.5亿立方米，2020年用水总量为5.265亿立方米．设该市用水总量的年平均降低率是x，那么x满足的方程是（    ）A．     B．C．     D．8．已知二次函数，其函数y与自变量x之间的部分对应值如下表所示：x……－11245……y……m1pnm……则m与n的大小关系正确的是（    ）A．   B．   C．   D．二、填空题（共5小题，每小题3分，计15分）9．若点与点关于原点对称，则的值为______．10．二次函数的部分图象如图所示，已知图象经过点，且对称轴为直线，则关于x的一元二次方程的根是______．11．把抛物线向左平移1个单位后经过点，平移后所得到的抛物线解析式是______．12．如图，的直径AB垂直于弦CD，垂足为E．若，，则AC的长为______．13．二次函数的图象如图所示，给出下列五条结论：①；②；③；④；⑤；其中正确的结论是______．（把所有正确的结论的序号都填写在横线上）三、解答题（共13小题，计81分．解答应写出过程）14．（5分）解方程：．15．（5分）已知抛物线．（1）用配方法将化成的形式；（2）写出抛物线的开口方向，对称轴和顶点坐标．16．（5分）如图，与关于O点成中心对称，点E，F在线段AC上，连接BE、DF，且，求证：．17．（5分）如图，在平面直角坐标系中，已知三个顶点的坐标分别为，，．（1）画出绕点O逆时针旋转90°后得到的；（2）在（1）的条件下，分别写出点B、C的对应点、的坐标．18．（5分）往直径为68cm的圆柱形油槽内装入一些油以后，截面如图所示，若油面宽度，求油的最大深度．19．（5分）某二次函数的图象经过点，和．（1）求该二次函数解析式；（2）将该二次函数图象以x轴为对称轴作轴对称变换得到新的二次函数，请求出新的二次函数的解析式．20．（5分）如图，点O是等边内的一点，连接OB、OC，，将绕点C按顺时针旋转得到，连接OD，求∠ADO的度数．21．（6分）已知：关于x的方程．（1）求证：方程总有两个实数根；（2）当时，求方程的根．22．（7分）全球疫情爆发时，医疗物资极度匮乏，中国许多企业都积极的宣布生产医疗物资以应对疫情，某工厂及时引进了一条口罩生产线生产口罩．经调查发现，1条生产线最大产能是1500万个/天，若每增加1条生产线，每条生产线的最大产能将减少50万个/天．现该厂要保证每天生产口罩6500万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？23．（7分）如图，四边形ABDC是的内接四边形，AD是对角线，过点A作交DB的延长线于点E，．（1）求证：；（2）连接BC，若BC为的直径，求证：．24．（8分）为了美化环境，学校准备在如图所示的矩形ABCD空地上进行绿化，规划在中间的四边形MNPQ区域里种花，其余的四块三角形上铺设草坪，要求，已知米，米，设米，种花的面积为平方米，草坪面积为平方米．（1）分别求和与x之间的函数关系式（不要求写出自变量的取值范围）；（2）当AN的长为多少米时，种花的面积为640平方米？25．（8分）如图所示，的直径AB和弦CD相交于点E，且点B是的中点，连接BD、BF、EF．（1）求证：；（2）连接OD，已知，，，求CD的长．26．（10分）如图，已知抛物线，与x轴交于，两点，与y轴交于点C．点P是线段BC上一动点，过点P作x轴的垂线交抛物线于点D．（1）求抛物线的解析式；（2）连接CD，是否存在点P，使得是以PD为腰的等腰三角形，若存在，求出P点的坐标；若不存在，请说明理由． 周至县2021~2022学年度第一学期期中调研试题九年级数学参考答案及评分标准一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．A 2．C 3．D 4．A 5．B 6．C 7．B 8．D二、填空题（共5小题，每小题3分，计15分）9．－16 10．或 11．（填也正确）  12．6 13．②④⑤三、解答题（共13小题，计81分．解答应写出过程）14．解：原方程化为，∵，，，∴，∴，∴，．15．解：（1），即．（2）∵，∴抛物线开口向下，抛物线的顶点坐标为，对称轴为直线．16．证明：∵与关于O点成中心对称，∴，．∵，∴，即，在和中，∴（SAS），∴．17．解：（1）如图所示，即为所求．（2）由图知，，．18．解：如图，连接OB，过点O作于点D，交于点C．∵于点D，∴（cm）．∵的直径为68cm，∴cm，在中，（cm），∴（cm），即油的最大深度为18cm．19．解：（1）设抛物线的解析式为，把代入得，解得，∴抛物线解析式为．（2）将此抛物线沿x轴进行轴对称变换，得到的新抛物线的解析式是，即．20．解：由旋转的性质得，，，．∵为等边三角形，∴，∴，∴为等边三角形，∴．∵，∴，∴．21．（1）证明：∵，∴方程是关于x的一元二次方程，∴，∴方程总有两个实数根．（2）解：当时，方程为，∴，∴，∴，∴，．22．解：设应该增加m条生产线，则每条生产线的最大产能为万个/天，依题意，得：，解得：，，又∵在增加产能同时又要节省投入，∴，∴应该增加4条生产线．23．证明：（1）∵四边形ABDC是的内接四边形，∴，∵，∴．（2）连接BC，∵BC为的直径，∴，∵，∴，∴，∴，在和中，∴（ASA）．∴．24．解：（1）由题可知，米，∵米， 米，∴（米），（米）．∵在矩形ABCD中，，∴（SAS），（SAS），∴，．（2）根据题意，知，即，解得：，，故当AN的长为16米或20米时种花的面积为640平方米．25．（1）证明：∵B是的中点．∴，∴，∴，，∵在和中，∴（SAS）．（2）解：∵，，∴．∵AB是的直径，∴，．过O作于G，则，∵，，∴，由勾股定理得：，∴．26．解：（1）由题可知，抛物线为，与x轴交于，两点，∴将A，B两点代入抛物线，∴，解得：，故抛物线的解析式为．（2）存在，理由：由抛物线的表达式知，点，设直线BC的解析式为，将，两点代入，则，解得：，故直线BC的表达式为．设点，则点，则，①当时，过点P作于E，∵，，∴，∴为等腰直角三角形，∴，∵，∴，∴为等腰直角三角形，又∵，点P在第三象限，∴，，则，解得：（舍去）或，故点；②当时，由题可知轴，∴，∴，∴，即，∴，即，解得：（舍去）或，∴点P的坐标为，综上，点P的坐标为或