数学2 不等式的基本性质评课课件ppt

这是一份数学2 不等式的基本性质评课课件ppt，共23页。PPT课件主要包含了+12+1，你发现什么规律啦，情境互动，-23-2，不等式的基本性质，合作探究一，归纳概括，方向不变，同一整式，符号语言等内容，欢迎下载使用。

数学——人类共同的语言
1、理解并掌握不等式的基本性质。2、会运用不等式的基本性质。3、感受生活中数学的存在，体验学习的乐趣。
–1<3 -1+2____3+2 -1－3___3－3 -1+(-2)__3+(-2) -1-(-1)__3-(-1) -1+a____3+a -1－a____3－a
-2>-5-2+2____-5+2-2-2_ _-5-2-2+(-2) __-5+(-2)-2-(-1) __-5-(-1)-2+a__-5+a -2-a___-5-a
不等式性质1： 不等式两边加上（或减去） 不等号的
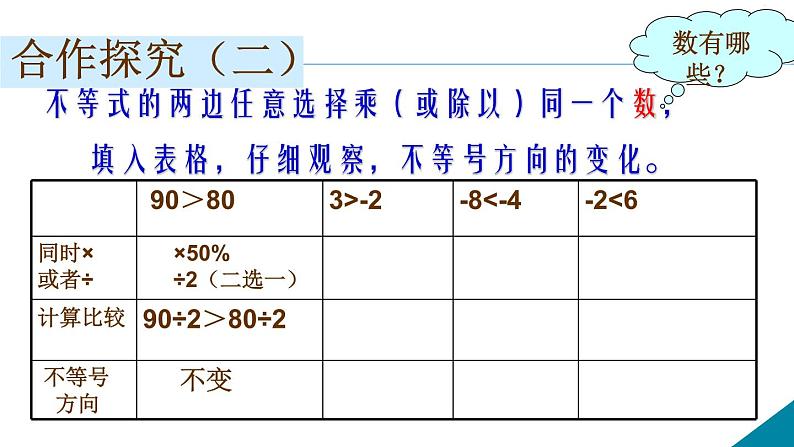
不等式的两边任意选择乘（或除以）同一个数，填入表格，仔细观察，不等号方向的变化。
不等式性质2：不等式两边乘以（或除以）同一个 不等号的
不等式性质3 ： 不等式两边乘以（或除以）同一个 不等号的
加减都用性质1，不等号方向不改变乘除正数性质2，不等号方向还不变乘除负数性质3，不等号方向要改变
1、如果a>b，用“>”“<”填空 （1）2+a _____ 2+b （不等式性质 ___） （2）a-3 _____ b-3 （不等式性质____） （3） 6a_____6b （不等式性质____） （4）-3a ____ -3b （不等式性质____）
2、判断正误，并说明理由：
若a+m>b+m，则a>b。 （ ）若-6a<-6 b,则a2b+1，则a>b。 （ ）由2x＜8，可得到x＜4。 （ ）
将下列不等式化成 或 的形式
解：根据不等式的基本性质___，两边都___,不等号方向___
将下列不等式化成 或 的形式:
要求：1.先独立完成上面的题目 2.再在小组内交流 3.小组长收集错例,总结注意事项
习题课上，老师在黑板上出了一道有关7a与6a比较大小的问题。小文不假思索说：“7a＞6a”。小明反驳道：“6a＞7a”。小芳说：“你俩答案都不全面，和在一起就对啦”。你认为他们三人的观点谁得正确，谈谈你的看法。
通过本节课的学习，你有哪些收获？
生活处处有数学在生活中应用数学
伟大的数学家毕达哥拉斯说过：在数学的天地里，重要的不是我们知道什么，而是我们如何知道什么。因此，学习数学一定要学会方法，学会如何去思考！
1.判断：如果a>b,下列不等式是否正确。（1）-4+a>-4+b （2）a-3-5b 2.填空：如果a>b,用“>”或“<”填空 （1）a+2__b+2；（2）a÷2__b÷2； （3）-8.5a+2__-8.5b+2；3、把下列不等式化成“x＞a”或“x＜a”的形式 （1）5x ＜ 4x-6 （2）-3x ＞ 27
必做题：《同步训练册》对应练习选做题：利用本节课所学，从生活中找出体现《不等式基本性质》的例子，表演情景剧，明天课上与大家分享。
若a>b,c<0.用不等号填空
a÷3＿＿ b÷32a-4 ＿＿2b-4-a ＿＿-bac ＿＿bc ac+c ＿＿bc+c
选择恰当的不等号填空，并说出理由。
（1）若-a＞-b，则2-a＿＿2-b； （2）若-a＜b，则a＿＿-b；（3）若a＞-b，则a+b＿＿0； （4）若a-b＞a，则b＿＿0．
b+a___c+a
ba __ ca
∵4a＜8a ∴a是___数∵2a＞3a， ∴a是___数∵ax＜a且x＞1 ∴a是___数