2023届上海市青浦高级中学高三上学期期中数学试题含解析

这是一份2023届上海市青浦高级中学高三上学期期中数学试题含解析，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
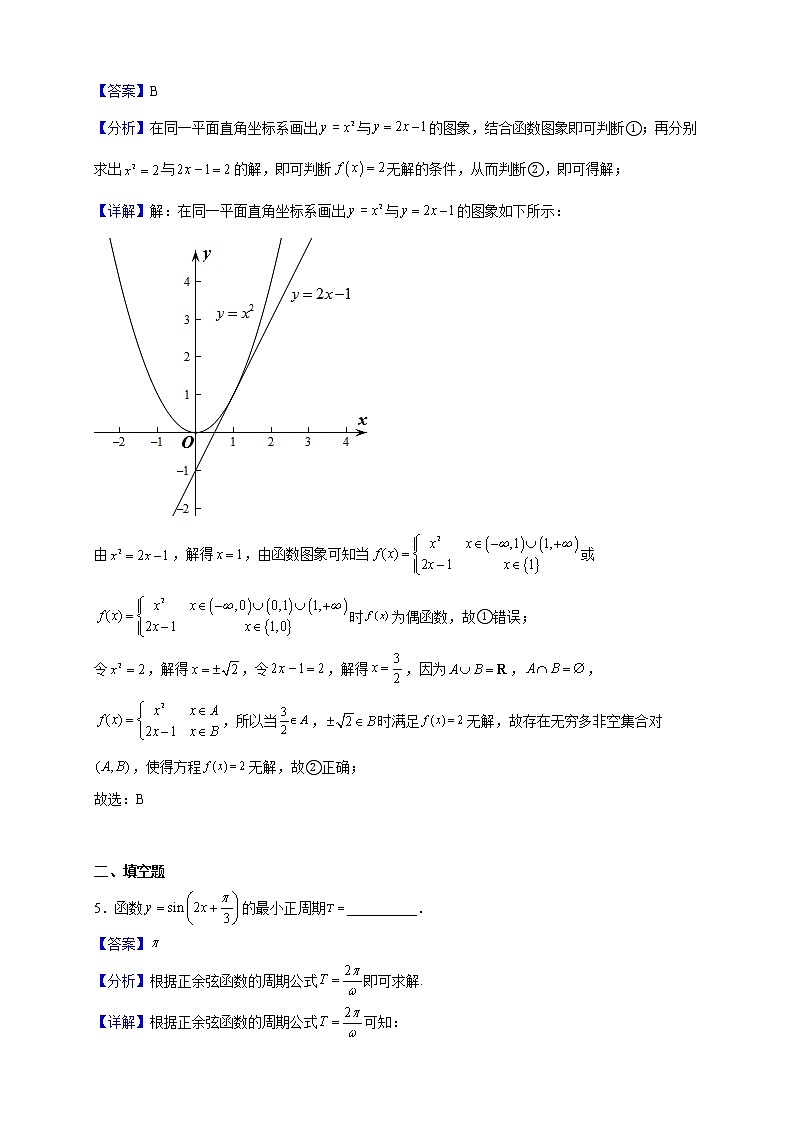
2023届上海市青浦高级中学高三上学期期中数学试题 一、单选题1．下列函数中，既是偶函数，又是在区间上单调递减的函数为（ ）A． B． C． D．【答案】A【详解】试题分析：由偶函数定义知，仅A,C为偶函数， C. 在区间上单调递增函数，故选A．【解析】本题主要考查奇函数的概念、函数单调性、幂函数的性质．点评：函数奇偶性判定问题，应首先考虑函数的定义域是否关于原点对称．2．中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为，三角形的面积可由公式求得，其中为三角形周长的一半，这个公式也被称为海伦-秦九韶公式，现有一个三角形的边长满足，则此三角形面积的最大值为A． B． C． D．【答案】C【分析】由题意，p＝10，S，利用基本不等式，即可得出结论．【详解】由题意，p＝10，S8，∴此三角形面积的最大值为8．故选C．【点睛】本题考查三角形的面积的计算，考查基本不等式的运用，属于中档题．3．已知定义在上的奇函数满足 ， 且当 时， ， 则下列结论正确个数为（    ）①的一个周期为2       ② ③      ④图象关于直线对称A．1 B．2 C．3 D．4【答案】A【分析】由条件证明，由此判断①，④，根据已知条件结合奇函数的性质求，判断②，根据函数的单调性判断③，由此确定正确命题的个数.【详解】因为当 时， ，所以，因为，所以，所以，因为，所以2不是的周期，①错，因为，所以函数图象不关于直线对称，④错，因为，所以，即，因为函数的定义域为，且为奇函数，所以，所以，所以，②对，因为，所以，又，所以，因为在上的单调递增，又，所以，因为在上单调递增，又，所以，所以，因为当 时， ，函数在上单调递增，所以，又，所以，③错，所以正确的命题只有②，故选：A.4．已知非空集合A，B满足：，，函数，对于下列两个命题：①存在唯一的非空集合对，使得为偶函数；②存在无穷多非空集合对，使得方程无解.下面判断正确的是（    ）A．①正确，②错误 B．①错误，②正确C．①､②都正确 D．①､②都错误【答案】B【分析】在同一平面直角坐标系画出与的图象，结合函数图象即可判断①；再分别求出与的解，即可判断无解的条件，从而判断②，即可得解；【详解】解：在同一平面直角坐标系画出与的图象如下所示：由，解得，由函数图象可知当或时为偶函数，故①错误；令，解得，令，解得，因为，，，所以当，时满足无解，故存在无穷多非空集合对，使得方程无解，故②正确；故选：B 二、填空题5．函数的最小正周期__________．【答案】【分析】根据正余弦函数的周期公式即可求解.【详解】根据正余弦函数的周期公式可知：函数的最小正周期，故答案为：.6．方程的解为______.【答案】2.【解析】由对数的运算性质可转化条件为，即可得解.【详解】方程等价于，所以，解得.故答案为：2.【点睛】本题考查了对数方程的求解，考查了运算求解能力，属于基础题.7．已知集合，若，且，则实数a的取值范围为___________.【答案】【分析】由，列不等式组即可求解.【详解】因为，，则有，解得，故答案为：8．函数的单调递减区间是___________．【答案】【分析】根据复合函数单调性同增异减求得正确答案.【详解】，，解得或.函数的开口向上，对称轴是轴，在上递减，根据复合函数单调性同增异减可知的单调递减区间是.故答案为：9．已知，则_________.（精确到0.001）【答案】【分析】求导后将代入即可.【详解】由题，，所以，故答案为：10．不等式的解集为______.【答案】【分析】原不等式化为，进而利用函数的单调性得到解一元二次不等式，即可得答案；【详解】原不等式可化为：根据指数函数的增函数性质得：解得：故答案为：11．已知集合，，若，则的取值集合为_______【答案】【分析】由题意可知，分、两种情况讨论，分析出方程的解的情况，综合可求得实数的值.【详解】因为，则.①若，则，符合题意；②若，则，则或，解得或.综上所述，实数的取值集合为.故答案为：.12．如图，八卦桥（图1）是洛南县地标性建筑之一，它是一个八边形人行天桥，桥的中心处建有一座五层高的宝塔（图2），晚上宝塔上的霓虹灯流光溢彩非常美丽.某同学为了测量宝塔的高度，在塔底部同一水平线上选取了C，D两点，测得塔的仰角分别为45°和60°，C，D间的距离是12米.则宝塔的高度AB为_______米.（结果保留根号）【答案】.【分析】设出未知数，根据三角函数列出方程，求出答案.【详解】设米，则因为，所以米，因为米，所以米，由得：，解得：，故宝塔的高度AB为米故答案为：.13．已知，则_____.【答案】【分析】利用三角恒等变换以及诱导公式可求值.【详解】因为，又因为，所以，故答案为: .14．已知函数和的图像如图所示，则不等式的解集是_______【答案】【分析】由题意可得f（x）与g（x）的函数值的符号相同，结合函数的图象分类讨论求得x的范围，即为所求．【详解】函数的定义域为，（1）当0＜x＜1时，f（x）＜0，g（x）＞0，＜0，不符合；（2）当1≤x＜2时，f（x）≥0，g（x）＞0，≥0，符合；（3）当x＞2时，f（x）＞0，g（x）＜0，＜0，不符合；所以解集是，故答案为.【点睛】本题主要考查分式不等式的解法，函数的图象的应用，属于基础题．15．函数对任意的，有，设函数，且在区间上单调递增，若，则实数的取值范围为________【答案】【分析】判断的奇偶性和单调性，根据单调性和奇偶性，运用二次不等式的解法，即可求解．【详解】由题意，得，所以，所以是R上的奇函数，又由在区间上单调递增，所以在R上为单调递增函数，因为，所以，∴，即，即实数的取值范围是【点睛】本题主要考查了函数的单调性与奇偶性的综合应用，其中解答中根据函数的奇偶性的定义得到为奇函数，进而得出函数的单调性，转化为一元二次不等式求解是解答本题的关键，着重考查了转化思想，以及推理与论证能力，属于中档试题．16．用表示非空集合中元素的个数，设，若，则实数的取值范围为________【答案】【详解】分解因式，原问题即：有个不同的实数根，则有个不同的实数根，很明显不是方程的实数根，据此可得：，则函数与函数有个不同的交点，将对勾函数的图象向右平移个单位，再向上平移个单位，然后将轴下方的图象向上关于轴对称翻折即可得到函数的图象，绘制函数图象如图所示(注意到当时函数值)，考查临界条件，观察可得：，据此可知实数的取值范围为.点睛：函数零点的应用主要表现在利用零点求参数范围，若方程可解，通过解方程即可得出参数的范围，若方程不易解或不可解，则将问题转化为构造两个函数，利用两个函数图象的关系求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用． 三、解答题17．已知集合，，且．(1)若是的充分条件，求实数a的取值范围；(2)若命题“”为假命题，求实数a的取值范围．【答案】(1)(2) 【分析】（1）（2）解不等式后由题意列式求解，【详解】（1）由得，即，若是的充分条件，则，由解得，则a的取值范围是，（2）若，则或，解得或，而“”为假命题，故a的取值范围是18．在中，角，，的对边分别是，，，且.(1)求角的大小；(2)若，，求和的值.【答案】(1)(2)或 【分析】(1)根据二倍角公式可得，进而得到角的大小；(2)由余弦定理得到，配方得到，结合题干条件解方程组，得到最终结果.【详解】（1）由二倍角公式得到，化简得到， .（2）根据余弦定理得到 配方得到： 解得：或.19．已知函数且.(1)当时，求函数的极值；(2)当时，求函数零点的个数.【答案】(1)有极小值，无极大值(2)零点个数为1 【分析】（1）求出导函数，求出极值点，判断导函数的符号，然后求解函数的极值；（2）利用函数的导数，通过对参数分类讨论分析其单调性即可知函数的零点个数.【详解】（1）解：由题意得：，令，得或（舍去），当时，，函数单调递减；当时，，函数单调递增；所以函数有极小值，无极大值.（2）由（1）得.因为，①若，当时，，函数单调递增；当时，，函数单调递减；当时，，函数单调递增；所以有极大值，极小值，又，所以函数有1个零点.②若，则，所以函数单调递增，此时，所以函数有1个零点.③若，当时，，函数单调递增；当时，，函数单调递减；当时，，函数单调递增；所以有极大值，显然极小值，又，所以函数有1个零点.综上所述，当时，函数的零点个数为1.20．如图，A、B两地相距100公里，两地政府为提升城市的抗疫能力，决定在A、B之间选址P点建造储备仓库，共享民生物资，当点P在线段AB的中点C时，建造费用为2000万元，若点P在线段AC上（不含点A），则建造费用与P、A之间的距离成反比，若点P在线段CB上（不含点B），则建造费用与P、B之间的距离成反比，现假设P、A之间的距离为x千米，A地所需该物资每年的运输费用为万元，B地所需该物资每年的运输费用为万元，表示建造仓库费用，表示两地物资每年的运输总费用（单位:万元）．（1）求函数的解析式;（2）若规划仓库使用的年限为，，求的最小值，并解释其实际意义．【答案】（1）当，；当，；（2），见解析【分析】（1）由题意，设f（x）＝，由f（50）＝2000，求得k1与k2的值，则函数解析式可求；（2）求出g（x）＝2.5x+0.5（100﹣x）＝2x+50，然后分段写出H（x），求导后再对n分类求解H（x）的最小值，并解释其实际意义.【详解】解：（1）由题意，设f（x）＝，由f（50）＝2000，求得k1＝k2＝100000.∴f（x）＝；（2）g（x）＝2.5x+0.5（100﹣x）＝2x+50，若0＜x≤50，则H（x）＝f（x）+ng（x）＝，H′（x）＝，由H′（x）＝0，得x＝100，若n∈N*且n≤20，则H（x）在（0，50]上单调递减，H（x）min＝H（50）＝2000+150n；若n∈N*且n＞20，则H（x）在（0，100）上单调递减，在（100，50）单调递增，∴；若50＜x＜100，则H（x）＝f（x）+ng（x）＝，H′（x）＝＞0，H（x）在（50，100）上单调递增，若n∈N*且n≤20，则H（x）＞2000+150n；若n∈N*且n＞20，则H（x）＞50n+.综上，若n∈N*且n≤20，则H（x）min＝2000+150n；若n∈N*且n＞20，则.实际意义：当储备仓库使用年数不超过20年时，仓库建在C处，花费在建造仓库和两地物资运输总费用取最小值2000+150n；当储备仓库使用年数超过20年时，仓库建在A、C之间且与A相距处，花费在建造仓库和两地物资运输总费用取最小值.【点睛】本题考查根据实际问题选择函数模型，训练了利用导数求最值，是中档题.21．已知函数和的定义域分别为和，若对任意的，都恰好存在个不同的实数，使得（其中，则称为的“重覆盖函数”，如，是，的“4重覆盖函数”．(1)试判断，是否为，的“2重覆盖函数”，并说明理由；(2)若为,的“3重覆盖函数”，求实数的取值范围；(3)若，为，的“9重覆盖函数”，求的最大值．【答案】(1)不是，理由见解析；(2)(3)61 【分析】（1）当时，根据“重覆盖函数”的定义即可判断；（2）将问题转化为对于任意的，方程恰好有3个不同的根，然后分三种情况分别求解即可；（3）将问题转化成对于任意的，方程，在内有9个不同的根，利用数形结合的思想即可求解．【详解】（1）当时，，而,即只有唯一解，所以， 的“2重覆盖函数”；（2）因为,为增函数，所以,的值域为，故对于任意的，方程在内都恰好有个不同的根，①当时，，若，由，得，若，则，此时方程在内最多只有个不同的根，不合题意；②当时， 方程在内最多只有一个根，在内最多有两个根，所以在内有个不同的根，在内有两个根，因为，，所以，解得.③当时，在上单调递增，故方程需在内有2个不同根，在内有1个根，当时，，且，所以 ，解得，综上，实数的取值范围是；（3）因为函数，为单调递减函数，所以的值域为，对于任意的，方程，在内有9个不同的根，即与直线在轴右侧有9个不同的交点，由图可知，，即，由，得，解得，故的最大值为.【点睛】关键点点睛：根据函数的单调性结合函数图象是解题的关键．