







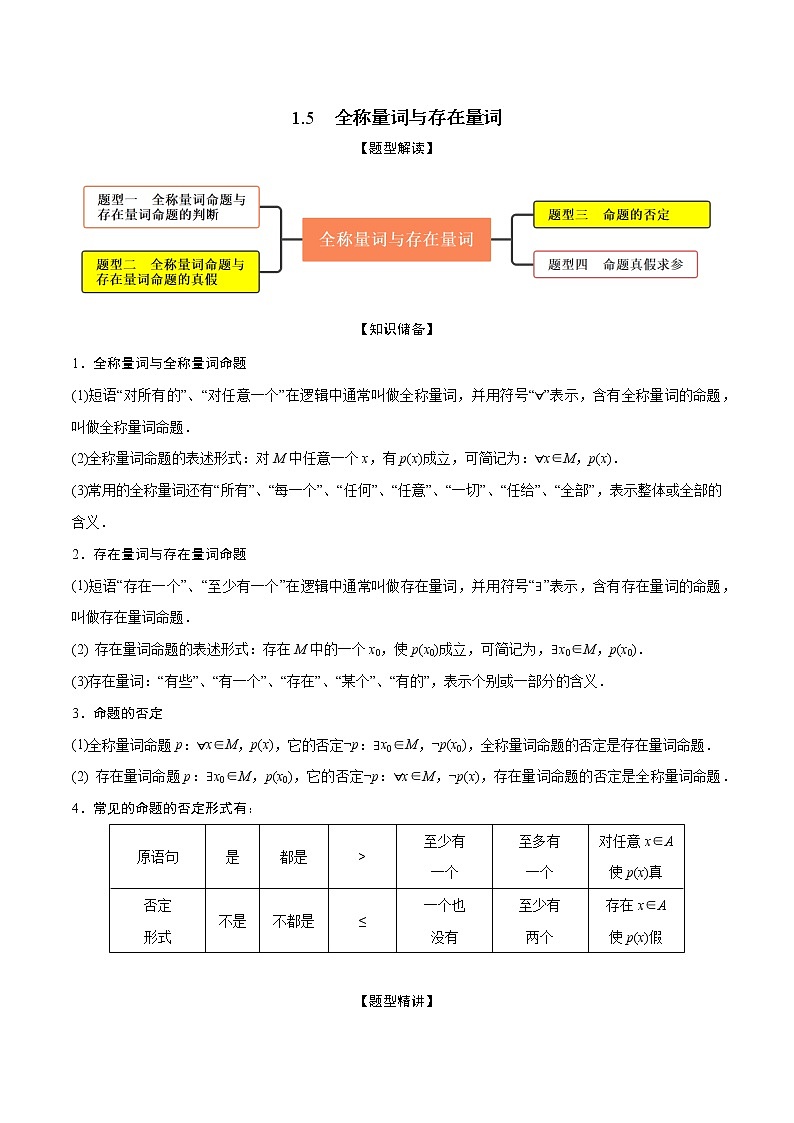





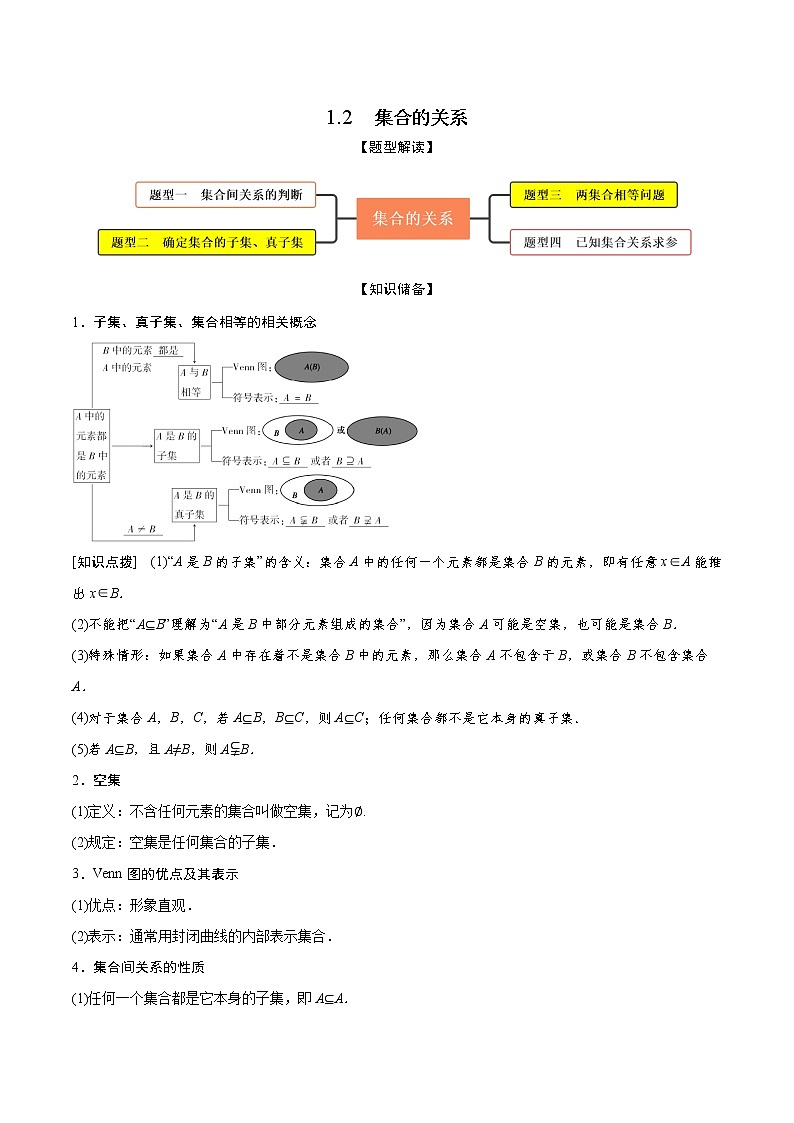


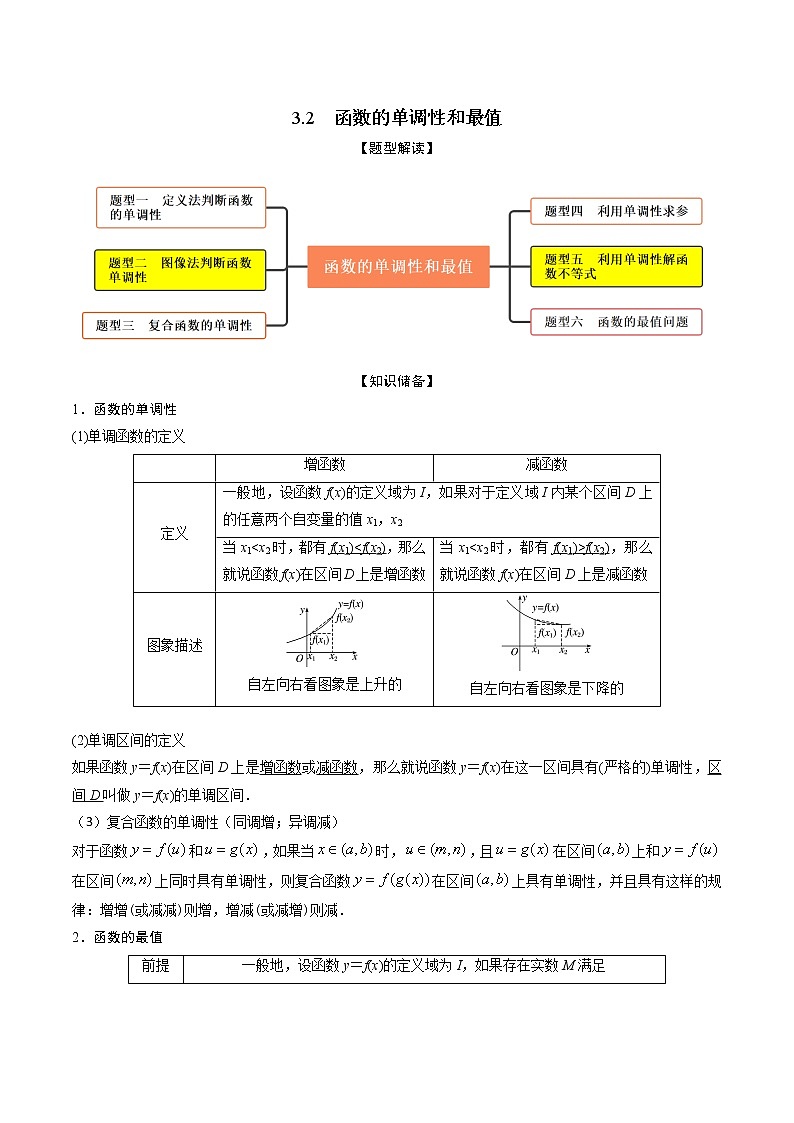









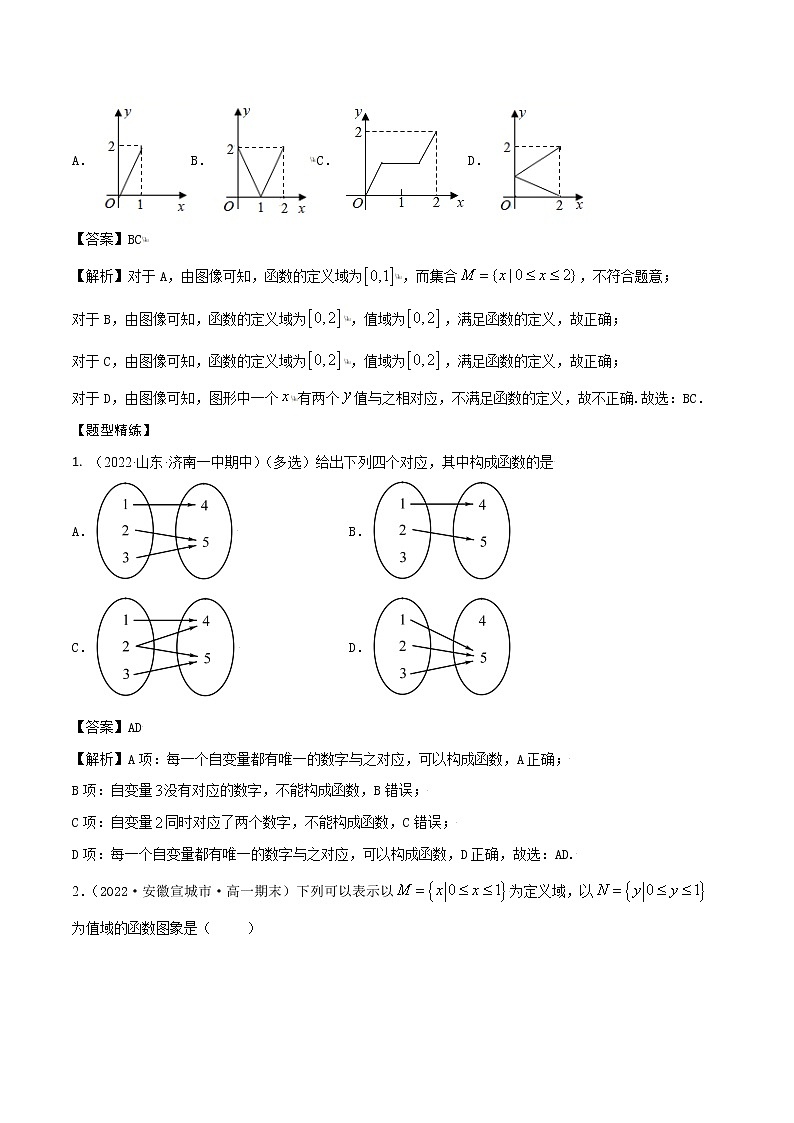






















所属成套资源:初升高暑假预科数学讲义课件
- 暑假新高一第一册预习培基同步讲义 其他 4 次下载
- 高一数学预科第一讲 等式及其性质 学案 学案 0 次下载
- 新高一暑假数学预习精练 课件 0 次下载
- (走进高一)初升高数学分层练习 试卷 5 次下载
- 高一暑假数学教学计划 其他 1 次下载
新高一暑假数学预习精讲
展开
这是一份新高一暑假数学预习精讲,文件包含31函数的概念及其表示精讲解析版docx、23二次函数与一元二次方程不等式精讲解析版docx、32函数的单调性和最值精讲解析版pdf、22基本不等式精讲解析版pdf、13集合的运算精讲解析版pdf、11集合的概念及表示精讲解析版docx、21等式与不等式的性质精讲解析版docx、12集合的关系精讲解析版docx、14充分条件与必要条件精讲解析版docx、15全称量词与存在量词精讲解析版docx、23二次函数与一元二次方程不等式精讲原卷版docx、31函数的概念及其表示精讲原卷版docx、13集合的运算精讲原卷版docx、15全称量词与存在量词精讲原卷版docx、21等式与不等式的性质精讲原卷版docx、11集合的概念及表示精讲原卷版docx、22基本不等式精讲原卷版docx、32函数的单调性和最值精讲原卷版docx、12集合的关系精讲原卷版docx、14充分条件与必要条件精讲原卷版docx等20份试卷配套教学资源,其中试卷共184页, 欢迎下载使用。
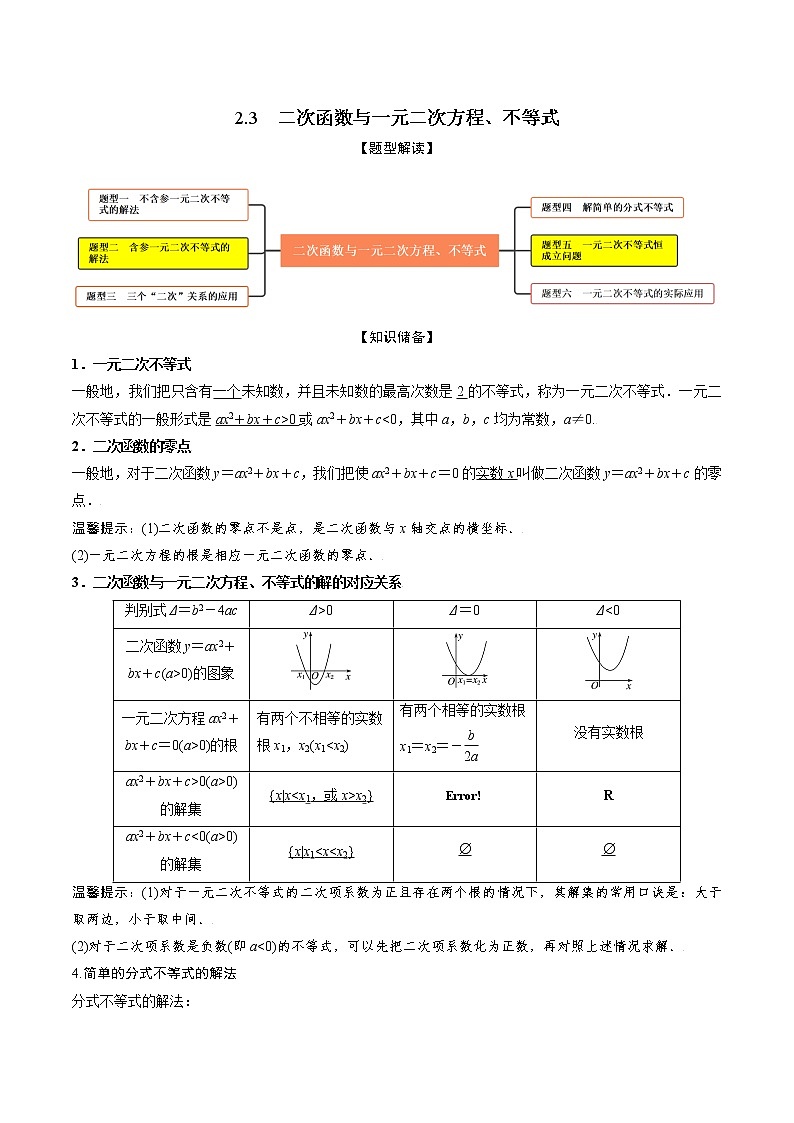
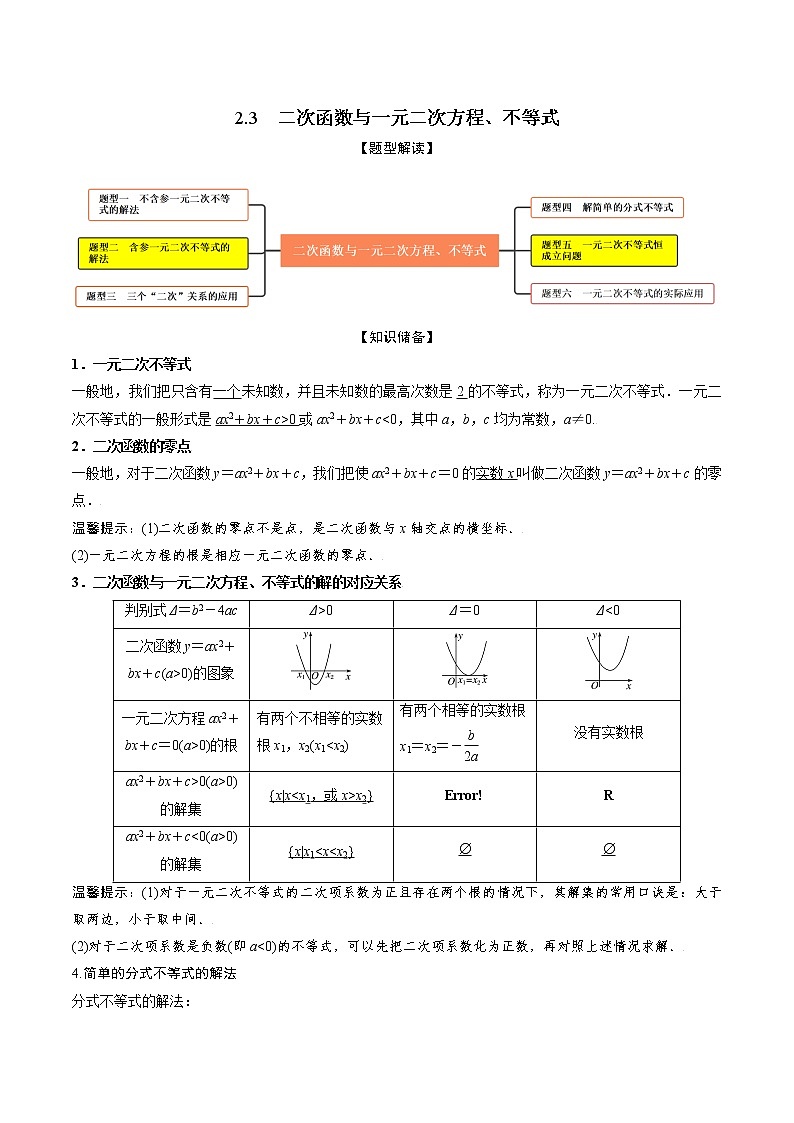
2.2 基本不等式【题型解读】【知识储备】1. 两个不等式重要不等式:当a、b是任意实数时,有a2+b2≥2ab,当且仅当a=b时,等号成立.基本不等式:当a>0,b>0时有≤,当且仅当a=b时,等号成立.叫做正数a,b的算术平均数,叫做正数a,b的几何平均数.基本不等式表明:两个正数的算术平均数不小于它们的几何平均数.温馨提示:“当且仅当a=b时,等号成立”是指若a≠b,则a2+b2≠2ab,≠,即只能有a2+b2>2ab,<.2.基本不等式与最值已知x,y都是正数,(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值2;(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值S2.温馨提示:从上面可以看出,利用基本不等式求最值时,必须有:(1)x、y>0,(2)和(积)为定值,(3)存在取等号的条件.【题型精讲】【题型一 对基本不等式的理解】方法技巧 对基本不等式的理解(1)不等式成立的条件:a,b都是正数.(2)“当且仅当”的含义:①当a=b时,≥的等号成立,即a=b⇒=;②仅当a=b时,≥的等号成立,即=⇒a=b.例1 (2022·黑龙江·哈尔滨三中高一月考)下列说法中错误的是( )A.不等式a+b≥2恒成立 B.若a,b∈R+,则2 C.若a,b∈R+,满足a+2b=1,则8 D.存在a∈R,使得a2成立 例2 (多选)(2022·衡水市第十三中学高一月考)已知正数,,则下列不等式中恒成立的是( )A. B.C. D. 【题型精练】1. (2022·宁夏·银川一中期中)下列不等式恒成立的是( )A. B.C. D. 2.(多选题)(2022•海南高一期末)下列说法中正确的有( )A.不等式恒成立 B.存在a,使得不等式成立 C.若a,b∈(0,+∞),则 D.若正实数x,y满足x+2y=1,则【题型二 直接法求最值】例3 (2022·甘肃酒泉·高一期中)若实数a,b满足,则ab的最大值为( )A.2 B.1 C. D. 例4 (2022·河北·高一期末)已知,,,且,,则的最小值是( )A.3 B.4 C.5 D.6 【题型精练】1.(2022·湖北十堰期末)设x>0,y>0,则x+4y的最小值为 . 2. (多选)(2022·河北石家庄期中)设正实数m,n满足,则下列说法正确的是( )A.上的最小值为2 B.的最大值为1C.的最大值为4 D.的最小值为 【题型三 凑配法求最值】必备技巧 通过配凑法利用基本不等式求最值的策略拼凑法的实质在于代数式的灵活变形,拼系数、凑常数是关键,利用拼凑法求解最值应注意以下几个方面的问题:(1)拼凑的技巧,以整式为基础,注意利用系数的变化以及等式中常数的调整,做到等价变形;(2)代数式的变形以配凑出和或积的定值为目标;(3)拆项、添项应注意检验利用基本不等式的前提. 例5 (2022·山西·怀仁市第一中学校月考)设实数满足,则函数的最小值为( )A.3 B.4 C.5 D.6 例6 (2022·上海虹口·高一期末)已知,则的最大值为______. 【题型精练】1.(2022·北京大兴·高一期末)当时,的最大值为( )A. B. C. D. 2. (2022·全国·高一专题练习)(1)求函数的最小值及此时的值;(2)已知函数,,求此函数的最小值及此时的值. 【题型四 “1”的代换法求最值】必备技巧 “1”的代换法求最值(1)根据已知条件或其变形确定定值(常数);(2)把确定的定值(常数)变形为1;(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积的形式;(4)利用基本不等式求解最值. 例7 (2022·河南·夏邑第一高级中学高一期末)已知,则的最小值是( )A.2 B. C.4 D. 例8 (2022·安徽·南陵中学高一月考)若实数,满足,则的最小值为( )A. B. C. D. 【题型精练】1.(2022·安徽·高三阶段练习)已知,,,则的最小值是( )A.1 B.2 C.4 D.62. (2022·全国高一课时练习)已知,,则的最小值为_______________; 【题型五 二次商式求最值】例9 (2022·全国·高一课时练习)求下列函数的最小值(1);(2). 例10 (2022·江西·宁冈中学高一月考)的最大值为______. 【题型精练】1.(2022·全国·高一课时练习)函数的最大值为( )A.3 B.2 C.1 D.-1 2. (2022·全国·高一课时练习)若 ,则有( )A.最大值 B.最小值 C.最大值 D.最小值 【题型六 基本不等式求参】例11 (2022·全国·高一课时练习)若两个正实数,满足且存在这样的,使不等式有解,则实数的取值范围是( )A. B.C. D. 例12 (2022•南开区校级月考)设x>0,y>0,且不等式(ax+y)()≥9恒成立,则正实数a的取值范围是( )A.0<a≤4 B.0<a≤2 C.a≥4 D.a≥2 【题型精练】1.(2022·全国·高一课时练习)已知,,若不等式恒成立,则m的最大值为( )A.10 B.12 C.16 D.9 2. (2022·全国高一课时练习)已知关于x的不等式在上恒成立,则实数a的最小值为 ( )A.1 B. C.2 D. 【题型七 基本不等式的实际应用】例13 (2022·全国·高一课时练习)将一根铁丝切割成三段,做一个面积为,形状为直角三角形的框架,在下列4种长度的铁丝中,选用最合理共用且浪费最少的是( )A.6.5m B.6.8m C.7m D.7.2m 【题型精练】1.(2022·北京市十一学校高一期末)某公司要建造一个长方体状的无盖箱子,其容积为48m3,高为3m,如果箱底每1m2的造价为15元,箱壁每1m2造价为12元,则箱子的最低总造价为( )A.72元 B.300元 C.512元 D.816元
相关试卷
这是一份安老师新高一暑假数学预习精练,文件包含13集合的运算精练原卷版docx、11集合的概念及表示精练原卷版docx、31函数的概念及其表示精练原卷版docx、15全称量词与存在量词精练原卷版docx、32函数的单调性和最值精练原卷版docx、21等式与不等式的性质精练原卷版docx、23二次函数与一元二次方程不等式精练原卷版docx、12集合的关系精练原卷版docx、14充分条件与必要条件精练原卷版docx、22基本不等式精练原卷版docx、23二次函数与一元二次方程不等式精练解析版docx、22基本不等式精练解析版pdf、31函数的概念及其表示精练解析版docx、13集合的运算精练解析版pdf、21等式与不等式的性质精练解析版docx、11集合的概念及表示精练解析版docx、32函数的单调性和最值精练解析版pdf、15全称量词与存在量词精练解析版docx、14充分条件与必要条件精练解析版docx、12集合的关系精练解析版docx等20份试卷配套教学资源,其中试卷共169页, 欢迎下载使用。
这是一份新高一暑假数学培优教材,共87页。
这是一份第12讲 对数-新高一数学暑假精品课(苏教版必修第一册),文件包含第12讲对数解析版docx、第12讲对数原卷版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。









