数学九年级下册6.2 黄金分割说课课件ppt

这是一份数学九年级下册6.2 黄金分割说课课件ppt，共23页。PPT课件主要包含了×34，黄金三角形，请你欣赏，回头一看我想说，课后我们要做的是等内容，欢迎下载使用。

芭蕾舞演员身体各部分之间适当的比例给人以匀称、协调的美感。
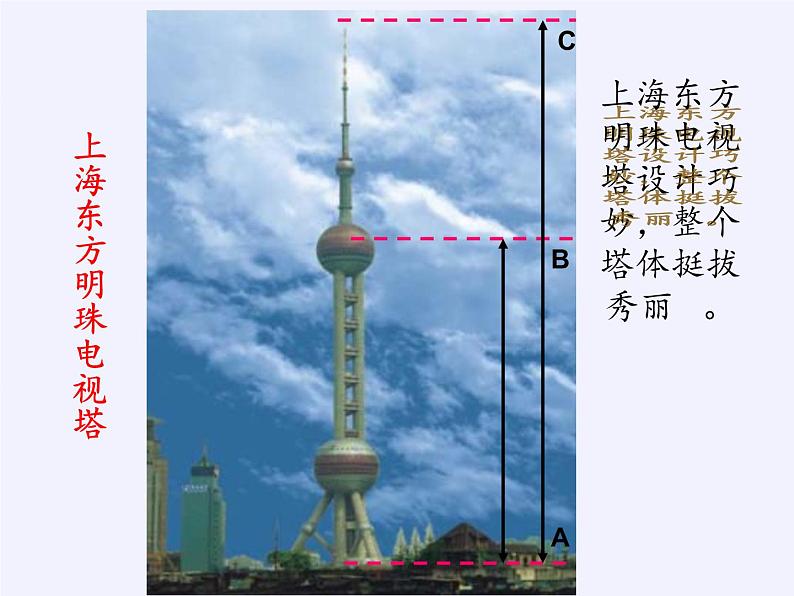
上海东方明珠电视塔设计巧妙，整个塔体挺拔秀丽 。
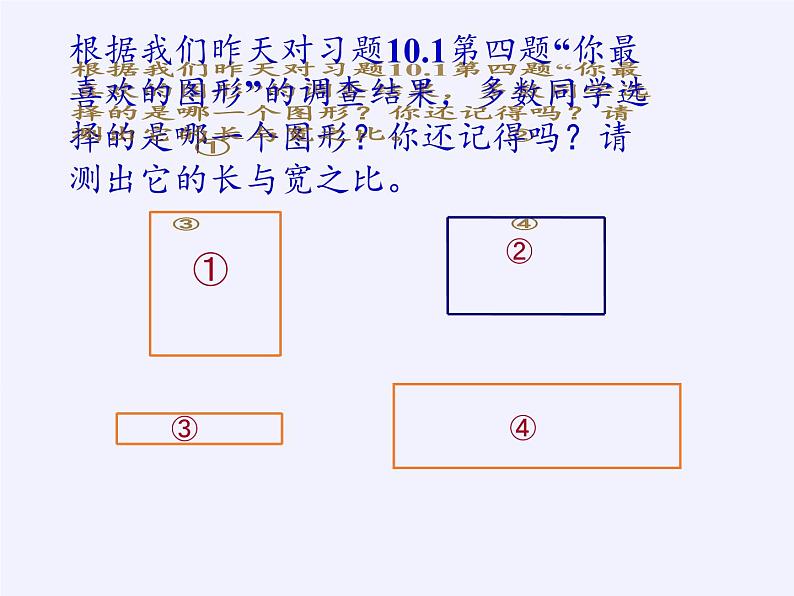
根据我们昨天对习题10.1第四题“你最喜欢的图形”的调查结果，多数同学选择的是哪一个图形？你还记得吗？请测出它的长与宽之比。
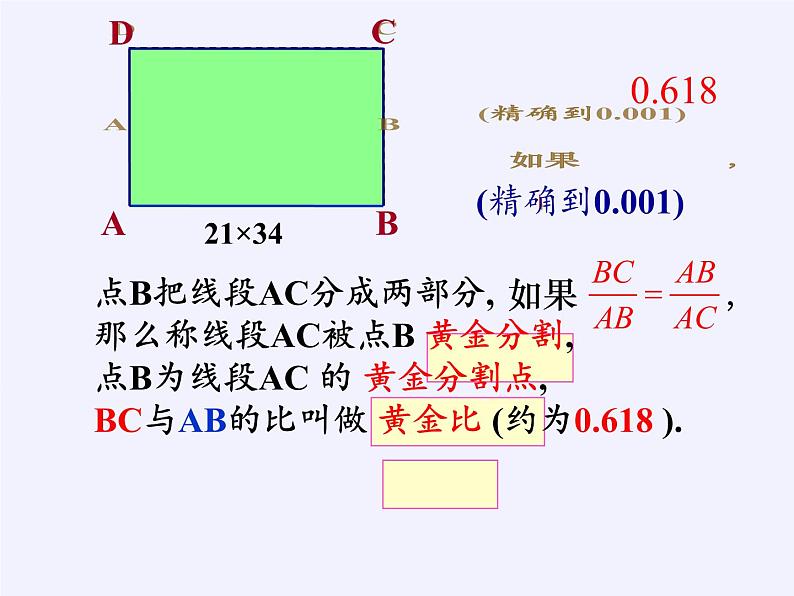
点B把线段AC分成两部分,那么称线段AC被点B 黄金分割,点B为线段AC 的 黄金分割点, BC与AB的比叫做 黄金比 (约为0.618 ).
例1 已知线段AB长20cm,若点M是线段AB的黄金分割点，则AM的长是多少？
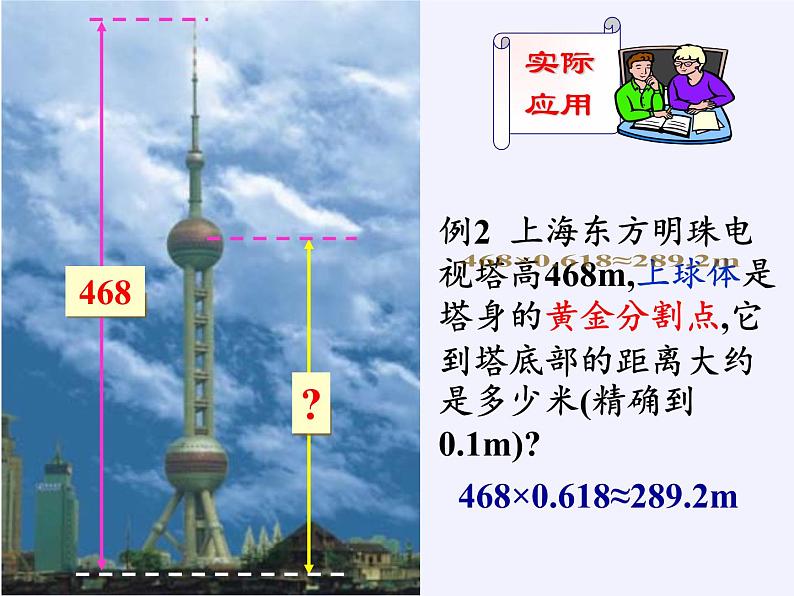
例2 上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468×0.618≈289.2m
例3 据有关测定, 当气温处于人体正常体温的黄金比值时 , 人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合? （人的正常体温36.2℃～ 37.2℃）
22.4℃～ 23.0℃
她的上半身和下半身的比值接近0.618.
世界艺术珍品——维纳斯女神
，她是西元前一百多年希腊雕塑鼎盛时期的代表作，
芭蕾舞演员的身段是苗条的，然而她们这个比值也只有0.58左右，于是人们设想：如果让演员在表演时 踮起脚尖，那么整个身高就可以增加 6～8cm,这时，肚脐以下部分与整个身长的比就可以接近黄金比0.618，从而给人以更优美的艺术形象……
若矩形的宽与长的比约为0.618,这样的矩形称之为黄金矩形.
上述的国旗中有共同图案吗？
1.作顶角为36°的等腰△ABC;量出 底BC与腰AB的长度,计算: ; 2.作∠B的平分线,交AC于点D,量出CD的长度, 再计算: . (精确到0.001)
☆顶角为36°的等腰三角形底边 与腰之比约为0.618;☆点D是线段AC的黄金分割点. ☆再作∠C的平分线,交BD于E, △CDE也是黄金三角形,……
如图,正五边形ABCDE的5条边相等,5个内角也相等.⑴找找看,图中是否有黄金三角形?
如图,正五边形ABCDE的5条边相等,5个内角也相等.⑴找找看,图中是否有黄金三角形?⑵点F是线段 , 的黄金分割点. 点G呢？
勾股定理和黄金分割是几何中的双宝,“前者好似黄金，后者堪称珠玉”。黄金分割的魅力远不止……
我有哪些收获呢？与大家共分享！
学 而 不 思 则 罔
☆收集身边的黄金分割的实例,与同伴谈 谈你对黄金分割的收获与体会；☆通过上网调查,了解黄金分割在现实生 活中的应用；☆完成一件包含黄金分割内容的作品。