初中数学苏科版九年级下册5.5 用二次函数解决问题教学演示课件ppt

这是一份初中数学苏科版九年级下册5.5 用二次函数解决问题教学演示课件ppt，共22页。PPT课件主要包含了归航拾贝，你的收获是，作业导学案，结束寄语等内容，欢迎下载使用。


（一）激情导入，提出问题
如图：在十八班足球队的魏鑫在训练中，在距球门12m处挑射，正好射中了2.4m高的球门横梁。若足球运行的路线是如图所示的抛物线 。通过图象你能得出哪些结论？
（二）设疑猜想，主动探究
体育课上，李童正和赵子琦打羽毛球。已知赵子琦打出的一球行进的高度 与水平距离 之间的关系是 。则羽毛球打出的最大高度是 米。
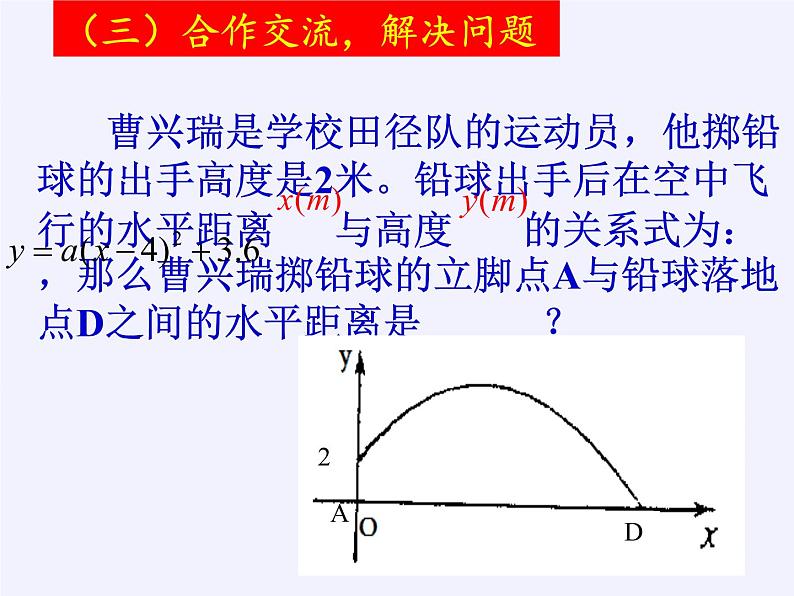
曹兴瑞是学校田径队的运动员，他掷铅球的出手高度是2米。铅球出手后在空中飞行的水平距离 与高度 的关系式为： ，那么曹兴瑞掷铅球的立脚点A与铅球落地点D之间的水平距离是______？
（三）合作交流，解决问题
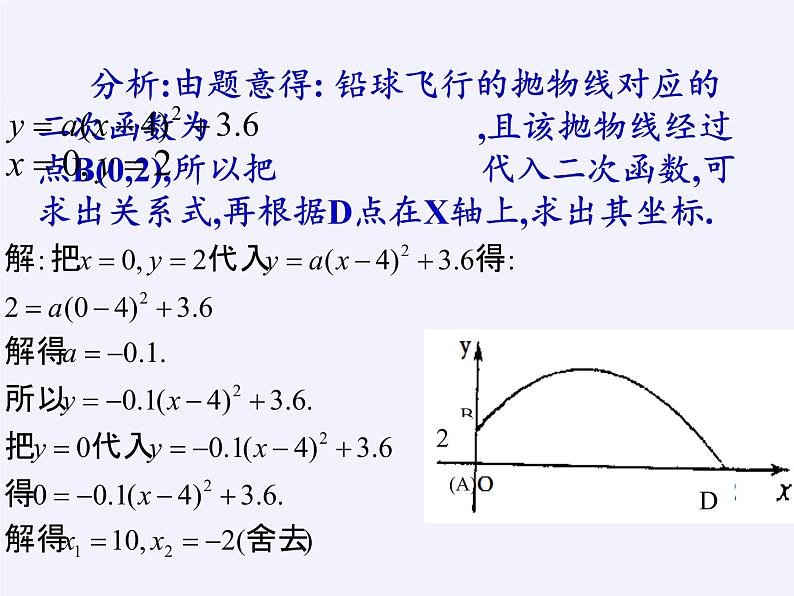
分析:由题意得: 铅球飞行的抛物线对应的二次函数为 ,且该抛物线经过点B(0,2),所以把 代入二次函数,可求出关系式,再根据D点在X轴上,求出其坐标.
(变)如图，学校的喷泉中喷头高出地面1.2米，如果喷出的抛物线形水流的水平距离 与高度 之间的关系为二次函数 ，求水流落地点D与喷头底部A的距离。
例1：如图，公园要建造圆形喷水池，在水池中央垂直于水面处安装一个柱子OA=1.25m，水流在各个方向沿形状相同的抛物线路线落下．（1）为了使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面的最大高度2.25m．若不计其他因素，则水池的半径至少要多少米才能使喷出的水流不致落到池外？（2）已知水流喷出的抛物线形状与（1）相同，水池的半径为3.5m，要使水流不落到池外，此时水流最大高度可达多少米？（精确到0.1m）
（1）建：恰当地建立直角坐标系；（2）设：合理地设出所求函数关系式；（3）化：将已知条件转化为点的坐标；（4）代：代入已知点坐标，求出关系式；（5）得：得出结论。
例2：如图，索航在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05米．已知索航身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？
如图，唐翔宇在相距2米的两棵树间拴了一根绳子，为她妹妹做了一个简易的秋千，两棵树拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的妹妹 距较近的那棵树0.5米时， 头部刚好接触到绳子，则 绳子的最低点距地面的 距离为 米．
（四）巩固升华，拓展提高
某校九年级的一场篮球比赛中，如图蒋新宇正在投篮，已知球出手时离地面高 m，与篮圈中心的水平距离8m．当球出手后离甲水平距离为4m时到达最大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m.（1）此球能否直接投中？（2）如果出手力度，角度都不变（即抛物线形状不变），蒋新宇出手的高度为多少时能将让球投中？
（五）反思评价，课外练习
老师寄语：数学来源于生活，生活是数学的源泉。