苏科版九年级下册5.5 用二次函数解决问题图片课件ppt

这是一份苏科版九年级下册5.5 用二次函数解决问题图片课件ppt，共17页。PPT课件主要包含了存在性问题，内容解读，问题探究，方法归纳，问题再思考，课后自主探究等内容，欢迎下载使用。
学习目标： 1.通过存在性问题的探讨，能快速、正确地求出二次函数的解析式，并能运用二次函数的性质和相关知识解决问题； 2. 通过存在性问题的探讨，进一步提升综合运用知识进行分析问题、解决问题的能力.
学习重点： 与相似有关的存在性问题、与面积有关的存在性问题.
学习难点： 问题的分析、解决能力和综合运用知识能力的提升.
存在性问题是指判断满足某种条件的事物是否存在的问题．这类问题知识覆盖面广，综合性强，题意构思精巧，解题方法灵活，对同学们分析问题和解决问题的能力要求较高，是近几年来各地中考的“热点”．存在性问题的一般思路：先对结论作出肯定的假设，然后由肯定假设出发，结合已知条件或挖掘出隐含条件，辅以方程思想等，进行正确的计算、推理，再对得出的结果进行检验，判断是否与题设、公理、定理等吻合．若无矛盾，则说明假设正确，由此得出符合条件的数学对象存在；否则，说明不存在．
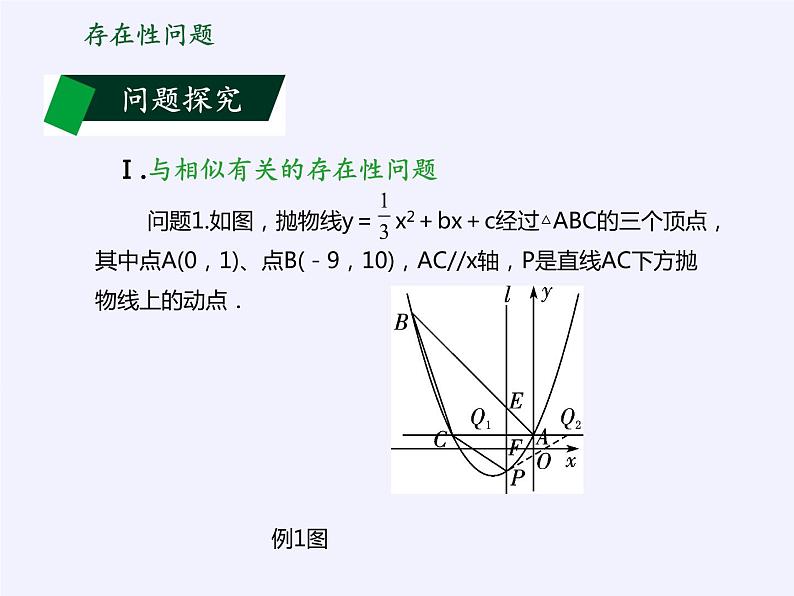
Ⅰ.与相似有关的存在性问题
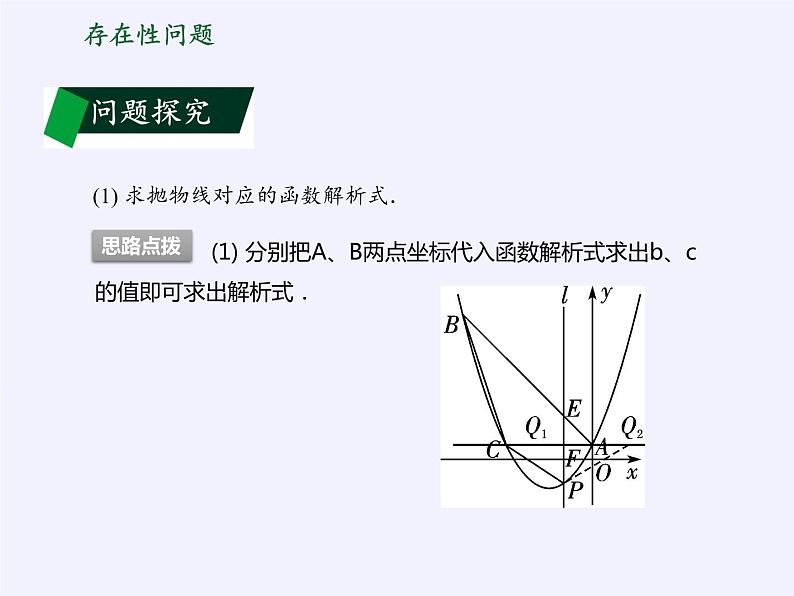
(1) 求抛物线对应的函数解析式．
(2) 过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标．
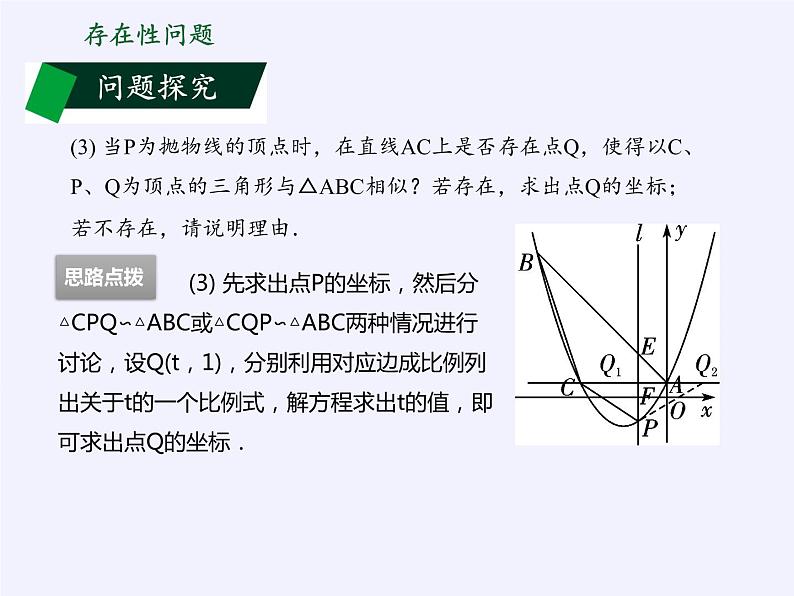
(3) 当P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．
(1) 求二次函数的解析式有三种形式：交点式、一般式、顶点式，用待定系数法来求二次函数的解析式时，要注意根据题意选择合理形式来简化计算．(2) 求四边形的面积最大值，关键是利用数形结合思想，将四边形分割成两个三角形，然后利用这两个三角形面积的和解决，而求此四边形面积的最值，一般要转化为顶点式来求．(3) 要使题目所求的两个三角形相似，需进行分类讨论，避免出现漏解的情况．
问题2.已知抛物线y＝ax2－4a(a>0)与x轴相交于A、B两点(点A在点B的左侧)，点P是抛物线上一点，且PB＝AB，∠PBA＝120°，如图①所示．例2图
Ⅱ.与面积有关的存在性问题
(2) 设点M(m，n)为抛物线上的一个动点，且在曲线PA上移动．① 如图②，当点M在曲线PB之间(含端点)移动时，是否存在点M使△APM的面积为 ？若存在，求出点M的坐标；若不存在，请说明理由．
② 如图③，当点M在曲线BA之间(含端点)移动时，求|m|＋|n|的最大值及取得最大值时点M的坐标．
本题涉及用待定系数法求二次函数解析式、三角形面积公式、二次函数最值等知识，要注意将三角形面积分解成两个三角形面积求和；对于用坐标表示三角形的面积，还需要注意绝对值的化简计算，求最大值时借助于二次函数的性质解决问题．
1.结合课堂中的两个问题思考，当我们遇到二次函数存在性问题时，解题的一般思路怎样？应注意什么问题？ 2.完成课堂问题的解题过程.
《练案》P102 存在性问题.
与特殊图形的判定有关的存在性问题
如图，抛物线经过A(－1，0)、B(5，0)、C(0，－ )三点．(1) 求抛物线对应的函数解析式．
(3) 分点N在x轴下方或上方两种情况进行讨论．
(2) 在抛物线的对称轴上有一点P，使PA＋PC的值最小，求出点P的坐标．