数学九年级下册5.2 二次函数的图象和性质导学案

这是一份数学九年级下册5.2 二次函数的图象和性质导学案，共4页。学案主要包含了学习目标，学习过程等内容，欢迎下载使用。


【学习目标】
1．经历把函数y=ax2的图象沿x轴、y轴平移后得到y=a（x+m）2+k的图象的探究过程，进一步了解上述图象变换的实质是：图像的形状、大小都没有改变，只是位置发生了变化。
2．能通过平移函数y=ax2的图象画出函数y=a（x+m）2或y=a（x+m）2+k的图象。
3．经历探索二次函数y=ax2+bx+c的图象和性质的过程，进一步体会配方法的重要作用。
4．能通过配方确定二次函数y=ax2+bx+c的图象的开口方向、顶点坐标、对称轴。
【学习过程】
一、情景导学：
上节课，我们从观察、分析“图形上点的坐标的数量变化”与“图形的位置变化”的关系着手，用运动变化的眼光观察并发现了二次函数y=ax2+k、y=a（x+m）2的图象与二次函数y=ax2图象的平移关系，从而判断二次函数y=ax2+k、y=a（x+m）2的图象也是抛物线。
二次函数y=a（x+m）2+k的图象也是抛物线吗？它与二次函数y=ax2的图象有什么关系？二次函数y=ax2+bx+c的图象是抛物线吗？它有什么性质？
二、思考探索：
1．二次函数y=（x+1）2+2的图象是抛物线吗？
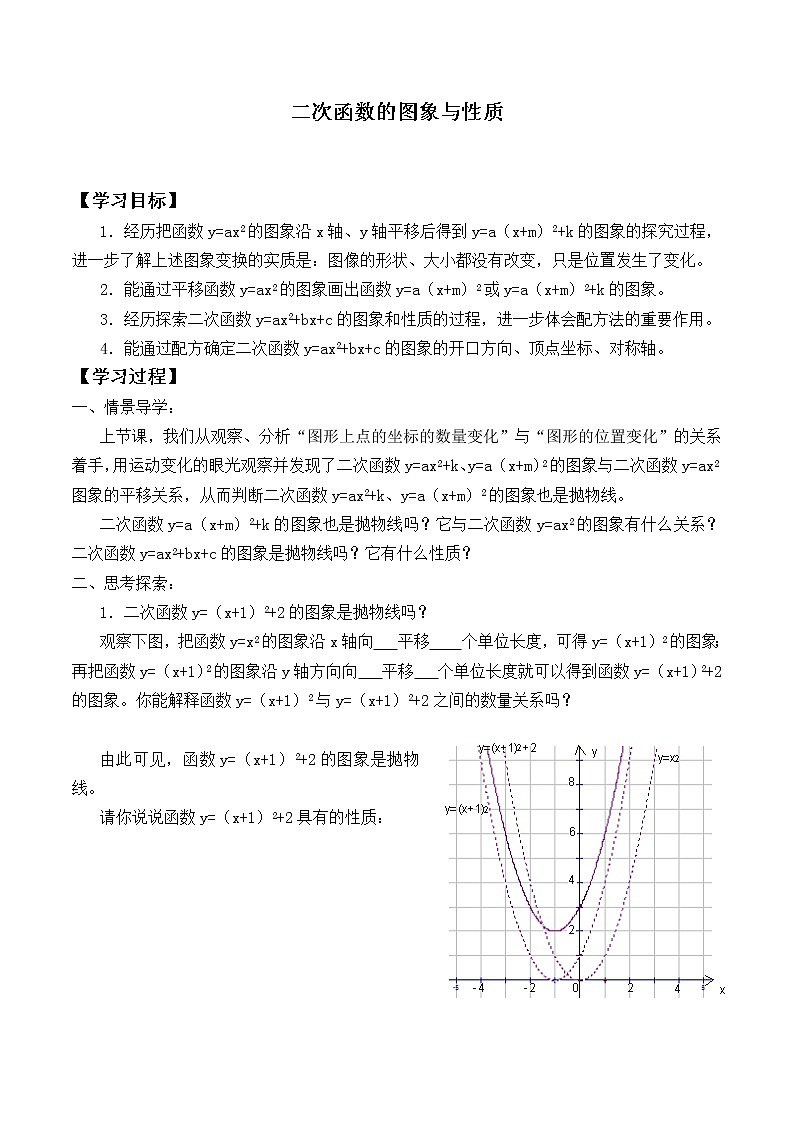
观察下图，把函数y=x2的图象沿x轴向 平移 个单位长度，可得y=（x+1）2的图象；再把函数y=（x+1）2的图象沿y轴方向向 平移 个单位长度就可以得到函数y=（x+1）2+2的图象。你能解释函数y=（x+1）2与y=（x+1）2+2之间的数量关系吗？
由此可见，函数y=（x+1）2+2的图象是抛物线。
请你说说函数y=（x+1）2+2具有的性质：
2．练习一：
（1）函数y=-2（x-2）2．y=-2（x-2）2+3的图象与函数y=-2x2的图象 都相同，只是 发生了改变，把函数y=-2x2的图象沿 轴向 平移 个单位长度，即可得到函数y=-2（x-2）2的图象；再将所得图象沿 轴向 平移 个单位长度，即可得到函数y=-2（x-2）2+3的图象。
（2）函数y=a（x+m）2+k的图象是由函数y=的图象向左平移1个单位长度，再向下平移2个单位长度得到的，则a= ；m ；k= 。
3．函数y=x2+2x+3的图象是抛物线吗？如果是，请你指出它是由哪个函数的图象怎样平移得到的？并说说它具有的性质。
4．练习二：
（1）说说怎样平移函数y=-2x2的图象才能得到函数y=-2x2+4x+1的图象？
（2）把下列函数化成顶点式，并写出它们的顶点坐标及最大值或最小值。
①y=x2-2x-3 ②y=-2x2-5x+7 ③y=3x2+2x ④y=
5．你能画出函数y=-x2-4x-6的图像吗？它有最大值还是有最小值？并求出它的最大值或最小值。
点拨：要画出二次函数y=-x2-4x-6的图象，可以先确定这个图象的顶点和对称轴的位置。你能确定这个图象的顶点和对称轴的位置吗？怎样确定？
根据图象的对称性，列表、描点连线如下：
请你求出它的最大值或最小值：
6．练习三：
画出函数y=的图象，并求出它的最大值或最小值。
7．你能判断二次函数y=ax2+bx+c的图象是抛物线吗？并总结它的性质。
8．练习四：
（1）根据y=ax2+bx+c=a（x++求下列函数的顶点坐标、对称轴、最大值或最小值：①y=x2-2x+4 ②y=x（8-x） ③y=100-5t2 ④y=（t-2）（2t+1）
（2）已知二次函数y=x2-5x+6，①当x为何值时，y随x的增大而增大？②当x为何值时，y随x的增大而减小？
（3）已知函数y=ax2+bx+c的图象与函数y=的图象的形状、大小、开口方向都相同，且顶点坐标是（-2，4），求a、b、c的值。
（4）已知函数y=。①确定该函数的图象的顶点在第几象限； ②如果该函数的图象经过原点，求它的顶点坐标。
（5）已知二次函数y=x2-（m-2）x+m+3．根据下列条件求m的值：①图象经过原点；②图像的对称轴是y轴；③图像的顶点在x轴上。
（6）已知二次函数y=（x+m）2+k的图象如图。
①根据图中提供的信息求二次函数的关系式；
②求图象与x轴的交点坐标；③观察图象解答：当x为何值时，y>0？y=0？y<0？
x
……
-4
-3
-2
-1
0
……
y
……
……
y=ax2+bx+c（a≠0）
a>0
a<0
开口方向
顶点坐标
对称轴
增减性
最值