数学九年级下册6.3 相似图形教学设计

课题：6.3相似图形

学习目标 ：

1．了解形状相同的图形是相似的图形；理解相似三角形、相似比的概念．

2．通过渗透类比的思想方法，进一步体会数学内容之间的内在联系，初步认识特殊与一般的辩证关系；通过几何图形的变换发展空间观念；通过从直观发现到自觉说理的过渡，培养有条理的表达能力。

3．经历观察、操作、归纳、类比、反思、交流的过程，提高数学思维水平；分析、欣赏相似图形，提高审美意识，增强学习数学的兴趣和自信心。

学习重点：相似三角形定义的理解和认识。

学习难点：准确判断出相似三角形的对应角和对应边。

学习过程：

一、创设情景，引入新课

1、放映电影时，屏幕上的画面是由放映机把底片上的画面经过放大后投射得到的，底片上的画面与屏幕上的画面形状是否相同?

2、同一张底片洗出来的不同尺寸的照片中，照片中物体的形状改变了吗?

二、合作交流，解读探究

1、思考：

（1）观察下面各组图形，说说它们有什么共同的特点？

（2）你能给具有上述特点的图形起个名字吗？

像这样，                的图形是            。

2、操作：

（1）度量图片上放大镜中的三角形和原三角形对应的角和边，你发现了什么？

（2）放大镜中的三角形和原三角形形状相同吗？它们相似吗？

3、归纳：

（1）相似三角形定义：各角对应          ，各边对应            的两个三角形叫做相似三角形。

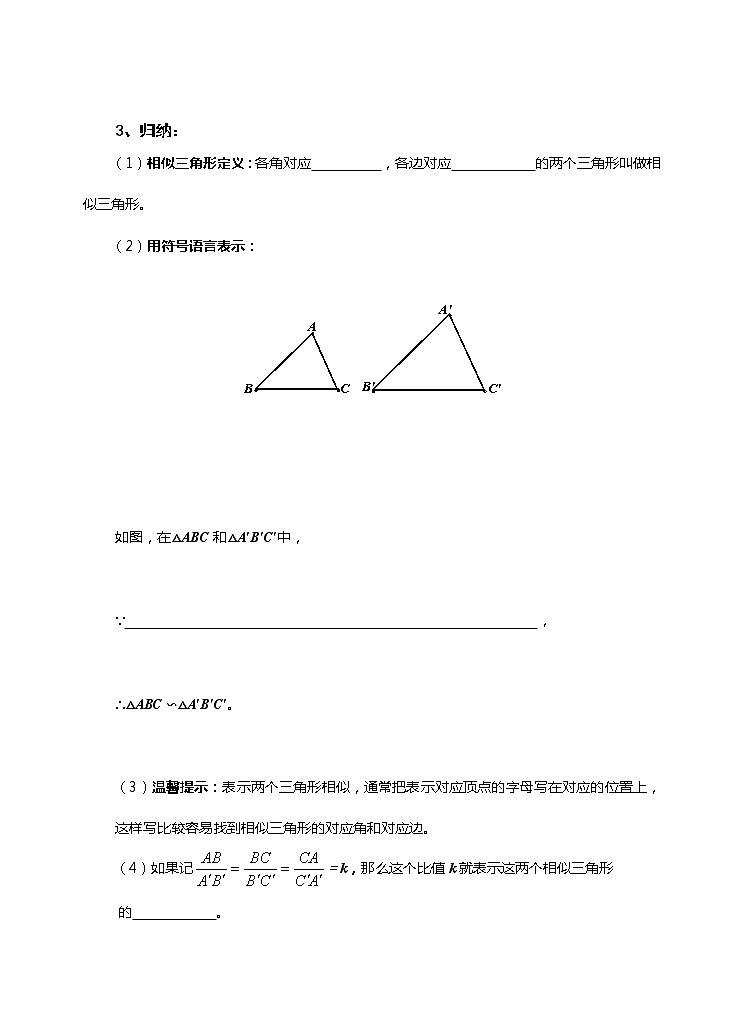
（2）用符号语言表示：

如图，在△ABC和△A′B′C′中，

∵                                                           ，

∴△ABC ∽△A′B′C′。

（3）温馨提示：表示两个三角形相似，通常把表示对应顶点的字母写在对应的位置上，这样写比较容易找到相似三角形的对应角和对应边。

（4）如果记＝k，那么这个比值k就表示这两个相似三角形

的            。

如果k=1，这两个三角形有怎样的关系？

4、性质：

（1反过来，我们可以得到相似三角形的性质：相似三角形的对应角         ，对应边             。

（2）用符号语言表示：

∵  △ABC ∽△A′B′C′，

  ∴                                                                 。

类似的，如果两个边数相同的多边形的各角对应        ，各边对应        ，那么这两个多边形相似，相似多边形的对应边的比叫做相似比。

三、应用新知，体验成功

进步的阶梯：

1.判断：

（1）所有的等边三角形都相似（    ）

（2）所有的矩形都相似      （    ）

2.分别根据下列已知条件，写出各组相似三角形的比例式：

(1)已知△ADE∽△ABC,则        =        =        ;

(2)已知△OAB∽△OCD,则        =        =        ; 

(3)已知△ABC∽△ADE,则        =        =        .     

3.如图，判断下面两个三角形是否相似，若相似，求出它们的相似比。

例1.如图所示，△ABC∽△A′B′C′，

求∠α的大小和A′C′的长；

   牛刀小试

1、如图， △ABC∽△ADE , AB=30cm, BD=18cm, BC=20cm,∠BAC=75 °,∠ABC=40°,

求:(1)∠ADE和∠AED的度数；                                

         (2)DE的长.

2、△ABC的三条边的长分别为6、8、10，与△ABC相似的△A'B'C'的最长边为30。则△A'B'C'的最短边的长为       。

  例2.如图，△ABC中，D、E分别是AB、 AC边的中点，

△ADE与△ABC 相似吗？为什么？

（1）若点F是BC边的中点，连接DF，△DBF与△ABC 相似吗？

（2）连接EF, △EFC与△ABC 相似吗？

（3）图中还有与△ABC相似的三角形吗？

四、总结反思，拓展延伸

1、说一说：

本节课我学会了                                                           ；

使我感触最深的是                                                         ；

我感到最困难的是                                                         ；

我想进一步探究的问题是                                                   。

2、试一试：

给出4个判断：①所有的等腰三角形都相似，②所有的等边三角形都相似，③所有的直角

三角形都相似，④所有的等腰直角三角形都相似。其中判断正确的个数有（    ）。   

 A. 1个       B. 2个        C.3个         D.4个