2022—2023学年 浙教版数学九年级上册期末检测模拟卷(含答案)

2022—2023学年度浙教版数学九年级上册期末检测模拟卷

一、单选题(共30分)

1．(本题3分)下列函数解析式中，一定为二次函数的是（   ）

A． B． C． D．

2．(本题3分)下列事件中，是不可能事件的是（    ）

A．随意翻到一本书的某页，这页的页码是奇数

B．篮球队员在罚球线上投篮一次，未投中

C．明天太阳从东方升起

D．任意画一个三角形，其内角和是360°

3．(本题3分)将抛物线先向右平移2个单位，再向下平移5个单位得到的抛物线所对应的函数解析式为（    ）

A． B．

C． D．

4．(本题3分)如图，在中，点，分别在，上，，如果，的面积为5，四边形的面积为15，那么的长为（　　）

A．8 B． C．6 D．

5．(本题3分)如图，E是正方形ABCD中CD边上的点，以点A为中心，把△ADE顺时针旋转，得到△ABF．下列角中，是旋转角的是（   ）

A．∠DAE B．∠EAB C．∠DAB D．∠DAF

6．(本题3分)为了估算河的宽度，我们在河对岸的岸边选定一个目标点记为点A，再在河近岸岸边选点 和点 ，使得 ，然后在河岸上选点 ，使得 ，设 与 交于点 ，如图所示，测得 米，米，米，那么这条河的大致宽度是（　　）

A．米 B．米 C．米 D．米

7．(本题3分)二次函数的图象如图所示，则直线不经过（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

8．(本题3分)已知，则=（　　）

A．2 B．- C．-1 D．

9．(本题3分)2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞，并于9时54分安全着陆，这标志着我国具备了按照国际通行适航标准研制大型客机的能力，如果某型号飞机降落后滑行的距离s（单位：米）关于滑行的时间t（单位：秒）的函数解析式是，则该飞机着陆后滑行最长时间为（　　）

A．243秒 B．486秒 C．18秒 D．36秒

10．(本题3分)如图，半圆O的直径AB＝2，若点C，D在半圆上运动，且保持弦CD＝1，延长AD、BC相交于点E．记∠E的度数为x°，△EDC的面积为y．则以下结论正确的是（    ）

A．x随C，D运动而变化，y随C，D运动而变化

B．x不随C，D运动而变化，y不随C，D运动而变化

C．x随C，D运动而变化，y不随C，D运动而变化

D．x不随C，D运动而变化，y随C，D运动而变化

二、填空题(共24分)

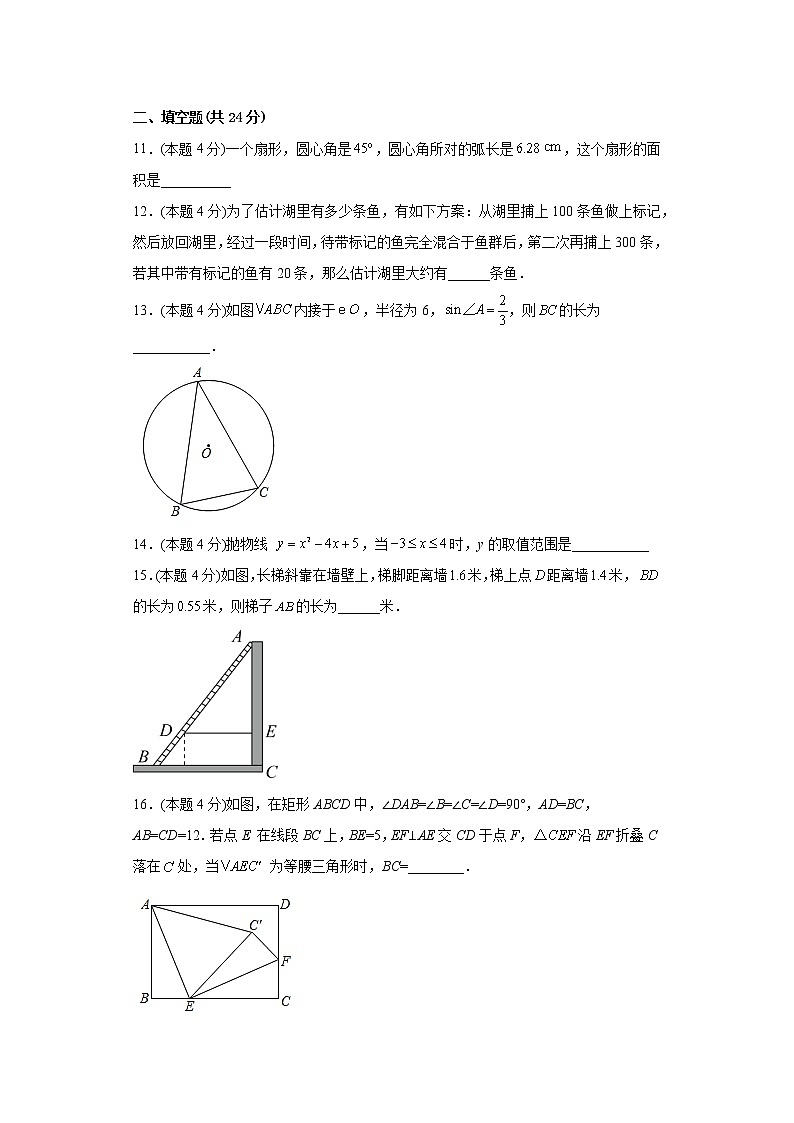
11．(本题4分)一个扇形，圆心角是，圆心角所对的弧长是，这个扇形的面积是__________

12．(本题4分)为了估计湖里有多少条鱼，有如下方案：从湖里捕上100条鱼做上标记，然后放回湖里，经过一段时间，待带标记的鱼完全混合于鱼群后，第二次再捕上300条，若其中带有标记的鱼有20条，那么估计湖里大约有______条鱼．

13．(本题4分)如图内接于，半径为6，，则的长为___________．

14．(本题4分)抛物线 ，当时，y的取值范围是___________

15．(本题4分)如图，长梯斜靠在墙壁上，梯脚距离墙米，梯上点距离墙米，的长为米，则梯子的长为______米．

16．(本题4分)如图，在矩形ABCD中，∠DAB=∠B=∠C=∠D=90°，AD=BC，AB=CD=12．若点E 在线段BC上，BE=5，EF⊥AE交CD于点F，沿EF折叠C落在处，当 为等腰三角形时，BC=________．

三、解答题(共66分)

17．(本题6分)如图，抛物线与y轴交于点．

(1)m的值为 　 　；

(2)当x满足 　 　时，y的值随x值的增大而减小；

(3)当x满足 　 　时，抛物线在x轴上方；

(4)当x满足时，y的取值范围是 　 　．

18．(本题8分)小明和小亮玩一个游戏： 三张大小、质地都相同的卡片上分别标有数字 1，2，3， 现将标有数字的一面朝下， 小明从中任意抽取一张后， 小亮再从剩下的卡片中抽取一张． 计算小明和小亮抽得的两个数字之和， 如果和为奇数则小明胜， 和为偶数则小亮胜．

(1)请用列表法或树状图等方法求小明获胜的概率．

(2)你认为该游戏对双方是否公平？ 请说明理由．

19．(本题8分)如图，在△ABC中，，以腰为直径作半圆，分别交、于点、．

(1)若，求弧的长；

(2)连结，求证：．

20．(本题10分)第二十四届冬季奥林匹克运动会已于2022年在北京成功举办，跳台滑雪是北京冬奥会的比赛项目之一，近些年来冰雪运动也得到了蓬勃发展．如图是某跳台滑雪场地的截面示意图．平台AB长1米（即），平台AB距地面18米．以地面所在直线为x轴，过点B垂直于地面的直线为y轴，取1米为单位长度，建立平面直角坐标系，已知滑道对应的函数为．运动员（看成点）在 方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落过程中的某位置（忽略空气阻力）．设运动员飞出时间为t秒，运动员与点A的竖直距离为h米，运动员与点A的水平距离为l米，经实验表明：，．

(1)求滑道对应的函数表达式；

(2)当，时，通过计算判断运动员此时是否已落在滑道上；

(3)在试跳中，运动员从A处飞出，运动员甲飞出的路径近似看做函数图像的一部分，着陆时水平距离为，运动员乙飞出的路径近似看做函数图像的一部分，着陆时水平距离为，则______（填“＞”“＝”或“＜”）．

21．(本题10分)已知二次函数的图象经过点．

(1)求该二次函数的表达式；

(2)二次函数图象与轴的另一个交点为，与轴的交点为，点从点出发在线段上以每秒个单位长度的速度向点运动，同时点从点出发，在线段上以每秒个单位长度的速度向点运动，直到其中一点到达终点时，两点停止运动，求面积的最大值；

(3)在点、运动的过程中，是否存在使与相似的时刻，如果存在，求出运动时间，如果不存在，请说明理由．

22．(本题12分)如图，抛物线与x轴相交于A，B两点，与y轴相交于点C．点D是直线AC下方抛物线上一点，过点D作x轴的垂线，垂足为E，与直线AC相交于点F．

(1)求直线AC的解析式；

(2)当线段DF的长度最大时，求点D的坐标．

23．(本题12分)如图，在中，，，，O是的中点，以O为圆心在的右侧作半径为的半圆O，分别交于点D、E，交于点G、F．

(1)求及弦的长．

(2)将线段连同半圆O绕点C旋转．

①求旋转过程中，点O到距离的最小值；

②若半圆O与的直角边相切时，设切点为K，连接，直接写出的长．

参考答案：

1．A

2．D

3．D

4．C

5．C

6．C

7．A

8．D

9．C

10．D

11．

12．

13．8

14．

15．

16．18或15或21.9

17．（1）解：把点代入抛物线的关系式得：．

故答案为：3．

（2）解：把代入得：

，

对称轴为直线，

∵，

∴当时y的值随x值的增大而减小；

故答案为：．

（3）解：根据解析（1）可知，抛物线的关系式为：，

把代入得：，解得：，，

∴抛物线与x轴的两个交点坐标为：，，

∴结合函数图像可知，当时，抛物线在x轴上方；

故答案为：．

（4）解：结合函数图像可知，当时，y可以取最大值，且最大值为：

，

∵，

∴当时，函数有最小值，且最小值为：，

∴当时，y的取值范围是．

故答案为：．

18．（1）解：画树状图图下：

由树状图可知，所有等可能的结果共有中，其中结果是奇数的有种，

∴小明获胜的概率为；

（2）∵（和为奇数）；（和为偶数）；

∴该游戏对双方是不公平的．

19．（1）解：如图，连接，

∵，，

∴，

∵为直径，，

∴，

∴；

（2）解：如图，连接，，

∵是的直径，

∴，

∵，

∴，

又，

∴，

∴，

∵，

∴，

∴．

20．（1） 过

（2） ，

，

当时，

∵

∴落在滑道上．

（3）解：将与联立，

得：，

化简得： ，

解得： ， ，

可知 ；

同理，将将与联立，

得：，

化简得： ，

解得： ， ，

可知 ，

，

因此 ．

21．（1）把点代入得：，

解得：，

二次函数的表达式为：．

（2）过作于，如图：

在中，令得，令得，，

，，，

，，，

设运动时间为，则，，

，

，

，即，

，

，

，

当时，面积的最大值为．

（3）在点、运动的过程中，存在使与相似的时刻，理由如下：

，，

与相似只需为直角三角形，

当时，如图：

，，

，

是等腰直角三角形，，

，

解得；

当时，如图：

同理可知，

，

解得，

综上所述，的值为或．

22．（1）22．解：∵抛物线与x轴相交于A，B两点，与y轴相交于点C，令∴∴，可得，

解得或，

∴，．

令，得，

∴，

设直线的解析式为，

则有，

解得，

直线的解析式为；

（2）解：设点D的横坐标为m，则点D的纵坐标为，F的纵坐标为，

∴．

当时，有最大值，

当时，．

∴．

23．（1）∵在中，，，，

∴，且O是的中点，

∴，

过点O作交于H，

∴

∵，且，

∴，且

∴，

即，

∴点H与点F重合，

即，

过点O作，且O为圆心

∴，

∵在中，，，

∴，

∵在中，，

∴，

∴，

∴

（2）①当时，点O到的距离最小，

由三角形面积公式可得， ，

∴，

∴，

∴点O到的距离最小值是；

②当半圆O与相切时，如图2，设切点为K，连接，，则，

在中，，，

∴，

在中，，

∴，

当半圆O与相时，如图3，设切点为K，连接，

∴，

∴．

∴的长为或．