山东省烟台龙口市（五四制）2022-2023学年八年级上学期期末考试数学试题(含答案)

2022—2023学年第一学期期末阶段性测试

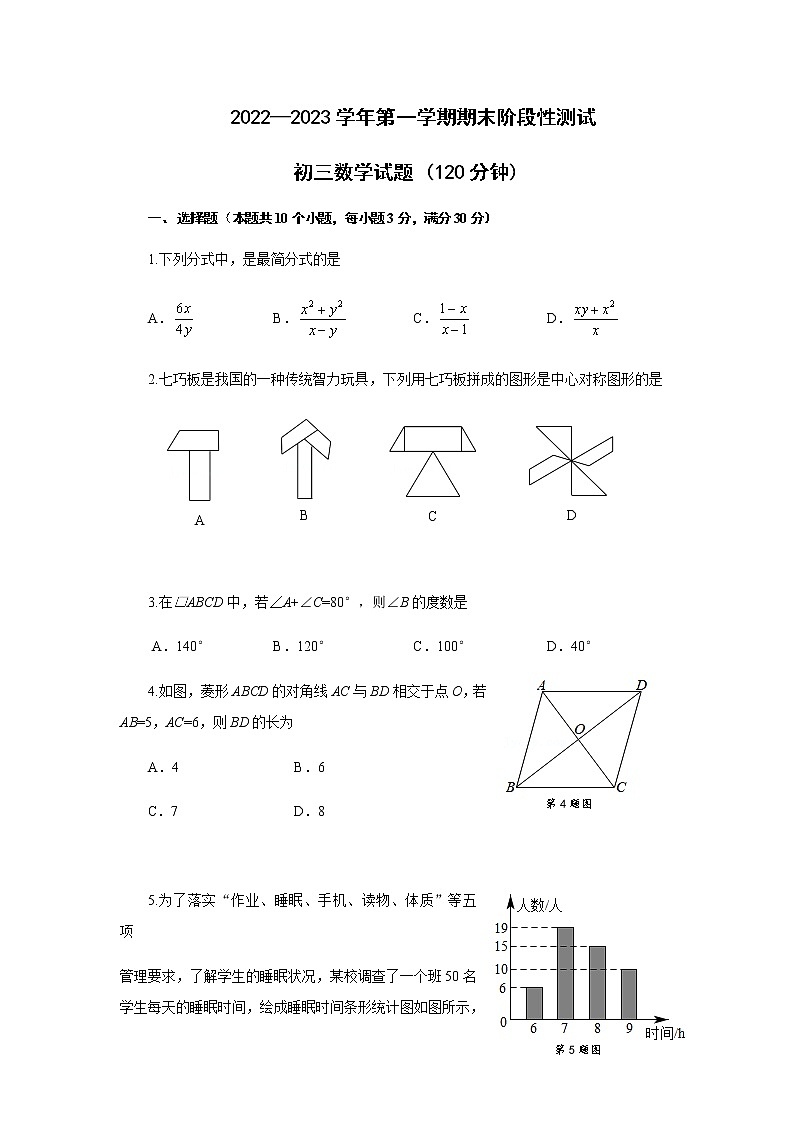
                       初三数学试题 (120分钟)

一、选择题（本题共10个小题，每小题3分，满分30分）

1.下列分式中，是最简分式的是

A． B． C． D．

2.七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形是中心对称图形的是

3.在□ABCD中，若∠A+∠C=80°，则∠B的度数是

A．140° B．120° C．100° D．40°

4.如图，菱形ABCD的对角线AC与BD相交于点O，若AB=5，AC=6，则BD的长为

A．4    B．6 

C．7    D．8

5.为了落实“作业、睡眠、手机、读物、体质”等五项

管理要求，了解学生的睡眠状况，某校调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图如图所示，则所调查学生睡眠时间的中位数为

A. 6h    B. 7h 

C. 7.5h    D. 8h

6.如图，将三角形纸片剪掉一角得四边形，

设△ABC与四边形BCDE的外角和的度数分别

为α，β，则正确的是

A．α=β           B．α＜β 

C．α＞β          D．无法比较α与β的大小

7.如图所示的扇形统计图描述了某校学生对课后延时

服务的打分情况（满分5分），则所打分数的众数为

A．5分  B．4分 

C．3分  D．45%

8.当m为自然数时，（4m+5）2-9一定能被下列哪个数

整除

A．5 B．6 C．7 D．8

9.如图，四边形ABCD是正方形，E为边CD上一点，△ADE绕着点A顺时针旋转

90°后到达△ABF的位置，连接EF，则△AEF的形状是

A．等腰三角形            B．直角三角形 

C．等腰直角三角形        D．等边三角形

10.如图，等腰直角三角形ABC中，∠ABC=90°，BA=BC，将BC绕点B顺时针旋转θ（0°＜θ＜90°），

得到BP，连接CP，过点A作AH⊥CP交CP的延长线于

点H，连接AP，则∠PAH的度数

A．随着θ的增大而增大 

B．随着θ的增大而减小 

C．保持定值45°不变 

D．随着θ的增大，先增大后减小

二、填空题（本大题共6个小题，每小题3分，满分18分）

11.如果关于x的方程有增根，那么m的值为         . 

12.若关于x的二次三项式x2+kx+9是完全平方式，则k的值是　      　．

13.已知一组数据x1，x2，x3的平均数和方差分别为5和2，则数据x1+1，x2+1，x3+1的平均数和标准差分别是　           　．

14.如图，在□ABCD中，AD=5，AB=3，∠BAD的平分线AE交BC于E点，则EC的长为            . 

15.如图，将长为5cm，宽为3cm的矩形ABCD先向右平移2cm，再向下平移1cm，得到矩形A'B'C'D'，则阴影部分的面积为　        　cm2．  

16.如图，在平面直角坐标系中，□ABCD三个顶点坐标分别为A（-1，-2），D（1，1），C（5，2），则顶点B的坐标为           .

三、解答题（本大题共9个小题，满分72分）

17.（本题满分6分）

分解因式：（1）a2（x-y）-4（y-x）．

（2）4（x+2）（x-3）+25

18.（本题满分5分）

解方程：

19.（本题满分6分）

先化简（-a+1）÷，然后从-2≤x≤2的范围内选择一个合适的整数作为x的值代入求值．

20.（本题满分6分）

如图，已知△ABC的三个顶点的坐标分别为A（-5，0）、B（-2，3）、C（-1，0）．

（1）画出△ABC关于原点O成中心对称的图形△A′B′C′；

（2）将△ABC绕原点O顺时针旋转90°，画出对应的△A″B″C″，并写出点B″的坐标．

21.（本题满分8分）

核酸检测时采集的样本必须在4小时内送达检测中心，超过时间，样本就会失效．A、B两个采样点到检测中心的路程分别为30km、36km．A、B两个采样点的送检车有如下信息：

信息一：B采样点送检车的平均速度是A采样点送检车的1.2倍；

信息二：A、B两个采样点送检车行驶的时间之和为2小时．

若B采样点从开始采集样本到送检车出发用了2.6小时，则B采样点采集的样本会不会失效？

22.（本题满分8分）

在学校组织的“文明出行”知识竞赛中，8（1）和8（2）班参赛人数相同，成绩分为A、B、C三个等级，其中相应等级的得分依次记为A级100分、B级90分、C级80分，其中8（2）班有2人达到A级，将两个班的成绩整理并绘制成如下的统计图，

请解答下列问题：

（1）求各班参赛人数，并补全条形统计图；

（2）此次竞赛中8（2）班成绩的中位数a为　    　分；

（3）小明同学根据以上信息制作了如下统计表：

请分别求出m和n的值，并从稳定性方面比较两个班的成绩．

23.（本题满分8分）

如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ADF：∠FDC=3：2，DF⊥AC交BC于F，垂足为E，求∠BDF的度数．

24.（本题满分11分）

如图，在□ABCD中，∠C=60°，M、N分别是AD、BC的中点．

（1）求证：四边形MNCD是平行四边形；

（2）若BC=2CD，MN=1，求BD的长．

25.（本题满分14分）

如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．

（1）判断四边形EFDG的形状是　           　（不必证明）；

（2）现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；

（3）如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．

2022-2023学年第一学期期末阶段性测试

初三数学参考答案及评分意见

一、选择题（每小题3分，共30分）

二、填空题（每小题3分，共18分）

11.-2，12.±6，13. 6，， 14.2，15.18， 16.（3，-1）．

三、解答题（17题每小题3分，18题5分，19-20题每小题6分，21-23题每小题8分，24题11分，25题14分，共72分）

17.解：（1）原式=a2（x-y）+4（x-y）=（x-y）（a2+4）.

（2）原式=4（x2-x-6）+25=4x2-4x-24+25=4x2-4x+1=（2x-1）2．

18.解：原方程可变为

方程两边同乘以x（x-2），得x-2-2=3x，解得x=-2，

检验：当x=-2时，x（x-2）≠0，

所以原分式方程的解为x=-2.

19.解：原式=[-]•==

=.

由分式有意义的条件可知a≠-1，a≠2，∴当a=0时，

∴原式=．（答案不唯一，如0，3）

20.解：（1）如图所示，△A'B'C'即为所求；

（2）如图所示，△A″B″C″即为所求，

其中点B″（3，2）．

21.解：设A采样点送检车的平均速度是xkm/h，

根据题意，得，

解得x=30，

经检验，x=30是分式方程的根，

∴B采样点送检车的平均速度为30×1.2=36（km/h），

∴B采样点送检车的行驶时间为36÷36=1（h），

∵2.6+1=3.6＜4，

∴B采样点采集的样本不会失效．

22.解：（1）∵8（2）班有2人达到A级，且A等级人数占被调查的人数为20%，

∴8（2）班参赛的人数为2÷20%=10（人）.

∵8（1）和8（2）班参赛人数相同，

∴8（1）班参赛人数也是10人，

故8（1）班C等级人数为10-3-5=2（人），

补全图形如右图：

（2）90；

（3）m=×（100×3+90×5+80×2）=91（分），

n=×[（100-91）2×3+（90-91）2×5+（80-91）2×2]=49，

∵8（1）班的方差大于8（2）班的方差，

∴从稳定性看8（2）班的成绩更稳定.

23.解：∵四边形ABCD是矩形，∴∠ADC=90°.

∵∠ADF：∠FDC=3：2，

∴∠FDC=×90°=36°.

∵DF⊥AC，∴∠DEC=90°.

∴∠DCO=90°-∠FDC=90°-36°=54°.

∵AC=BD，CO=AC，OD=BD，

∴CO=OD，

∴∠ODC=∠DCO=54°，

∴∠BDF=∠ODC-∠FDC=54°-36°=18°．

24.（1）证明：∵ABCD是平行四边形，

∴AD=BC，AD∥BC.

∵M、N分别是AD、BC的中点，

∴MD=NC.

∵MD∥NC，

∴四边形MNCD是平行四边形；

（2）如图，连接ND，

∵MNCD是平行四边形，∴DC=MN=1．

∵N是BC的中点，∴BN=CN=BC.

∵BC=2CD，

∴CD=CN.

∵∠C=60°，

∴△NCD是等边三角形，

∴ND=NC，∠DNC=60°．

∵∠DNC是△BND的外角，

∴∠NBD+∠NDB=∠DNC，

∵DN=NC=NB，

∴∠DBN=∠BDN=∠DNC=30°，

∴∠BDC=90°，

∴BC=2DC=2，

∴BD=.

25.解：（1）菱形；

（2）不变，

证明：由旋转得∠BAC=∠MAN，∴∠BAM=∠CAN，

∵AB=AC，AM=AN，∴△BAM≌△CAN（SAS），

∴BM=CN.

∵点E、F分别是MN、BN的中点，

∴EF∥BM，EF=BM，

同理，DG∥BM，DG=BM，FD=CN，

∴EF∥DG，EF=DG，

∴四边形EFDG是平行四边形.

且DG=FD.

∴四边形EFDG是菱形；

（3）添加条件：∠BAC=90°，

证明：如图，设BM与CN交于点P，DF与BM交于点Q，

由（2）得∠ABM=∠ACN，

∵∠BAC=90°，

∴∠ABC+∠ACB=90°，

∴（∠ABC-∠ABM）+（∠ACB+∠ACN）=90°，

即∠PBC+∠PCB=90°，

∴∠BPC=90°

∵DF∥CN，

∴∠BQD=90°.

∵DG∥BM，

∴∠FDG=90°，

∴菱形EFDG是正方形．