河南省新乡市2021-2022学年高一上学期期末考试数学试卷(含答案)

这是一份河南省新乡市2021-2022学年高一上学期期末考试数学试卷(含答案)，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

河南省新乡市2021-2022学年高一上学期期末数学试卷（解析版）
一、选择题：本题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．
1．某疫情防控志愿者小组有20名志愿者，由党员和大学生组成，其中有15人是党员，有9人是大学生，则既是党员又是大学生的志愿者人数为（　　）
A．2 B．3 C．4 D．5
2．命题“有些梯形的对角线相等”的否定是（　　）
A．有些梯形的对角线不相等
B．所有梯形的对角线都相等
C．至少有一个梯形的对角线相等
D．没有一个梯形的对角线相等
3．已知幂函数f（x）＝（3m2﹣11）xm在（0，+∞）上单调递减，则f（4）＝（　　）
A．2 B．16 C． D．
4．“α是第四象限角”是“是第二或第四象限角”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
5．现有两个相互啮合的齿轮，大轮有64齿，小轮有24齿，当小轮转一周时，大轮转动的弧度是（　　）
A． B． C． D．
6．某灯具商店销售一种节能灯，每件进价10元，每月销售量y（单位：件）与销售价格x（单位：元）之间满足如下关系式：y＝﹣10x+500（20＜x≤40且x∈N）．则灯具商店每月的最大利润为（　　）
A．3000元 B．4000元 C．3800元 D．4200元
7．函数的单调递增区间为（　　）
A．（11，+∞） B．（﹣∞，11） C．（23，+∞） D．（﹣∞，﹣1）
8．已知x＞0，y＞0，且x+2y＝2，则的最小值为（　　）
A．24 B．25 C．26 D．27
9．已知a＝0.590.61，b＝0.610.59，，则（　　）
A．a＜b＜c B．c＜a＜b C．c＜b＜a D．a＜c＜b
10．已知，则＝（　　）
A． B． C． D．
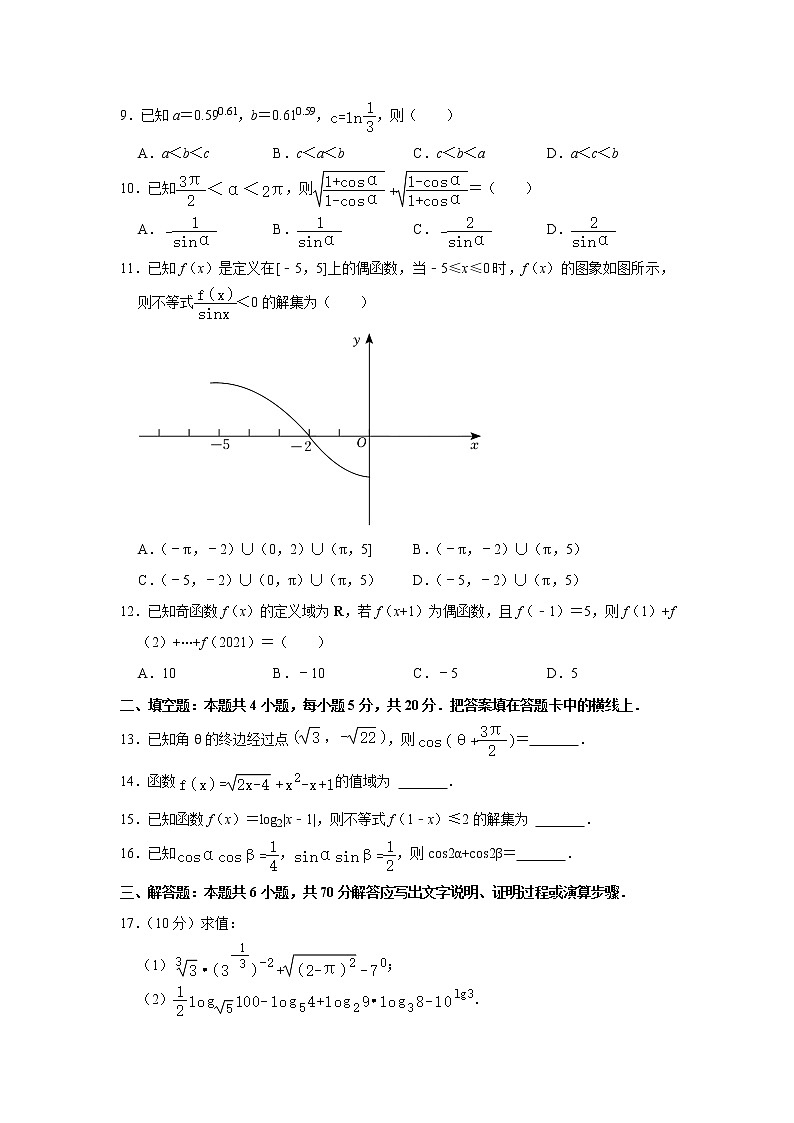
11．已知f（x）是定义在[﹣5，5]上的偶函数，当﹣5≤x≤0时，f（x）的图象如图所示，则不等式＜0的解集为（　　）

A．（﹣π，﹣2）∪（0，2）∪（π，5] B．（﹣π，﹣2）∪（π，5）
C．（﹣5，﹣2）∪（0，π）∪（π，5） D．（﹣5，﹣2）∪（π，5）
12．已知奇函数f（x）的定义域为R，若f（x+1）为偶函数，且f（﹣1）＝5，则f（1）+f（2）+⋯+f（2021）＝（　　）
A．10 B．﹣10 C．﹣5 D．5
二、填空题：本题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．
13．已知角θ的终边经过点，则＝　 　．
14．函数的值域为 　 　．
15．已知函数f（x）＝log2|x﹣1|，则不等式f（1﹣x）≤2的解集为 　 　．
16．已知，，则cos2α+cos2β＝　 　．
三、解答题：本题共6小题，共70分解答应写出文字说明、证明过程或演算步骤．
17．（10分）求值：
（1）；
（2）．
18．（12分）已知集合A＝{x|2a﹣2≤x≤a}，B＝{x|﹣3＜x＜1}．
（1）若a＝﹣2，求A∪（∁RB）；
（2）若A∩B＝A，求a的取值范围．
19．（12分）已知函数f（x）＝loga（x+2a）（a＞0且a≠1）的图象过点（3，2）．
（1）求a的值；
（2）若函数，求g（x）≥2的解集．
20．（12分）若将函数图象上所有点的横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度，得到函数g（x）的图象．
（1）求g（x）图象的对称中心；
（2）若，求的值．
21．（12分）已知函数．
（1）判断f（x）的奇偶性并说明理由；
（2）若对任意t∈R，k∈R，f（t2﹣t）+f（m﹣2t）＜k2恒成立，求m的取值范围．
22．（12分）已知函数f（x）＝sincos﹣sin2+sin（x+）+．
（1）将f（x）化为Asin（ωx+φ）（A＞0，ω＞0，）的形式；
（2）若函数g（x）＝a[f（x）]2﹣2f（x）+1在（）上有4个零点，求a的取值范围．

参考答案与试题解析
一、选择题：本题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．
1．某疫情防控志愿者小组有20名志愿者，由党员和大学生组成，其中有15人是党员，有9人是大学生，则既是党员又是大学生的志愿者人数为（　　）
A．2 B．3 C．4 D．5
【分析】党员人数和大学生人数之和减去志愿者小组总人数，得到既是党员又是大学生的志愿者人数．
【解答】解：某疫情防控志愿者小组有20名志愿者，由党员和大学生组成，
其中有15人是党员，有9人是大学生，
则既是党员又是大学生的志愿者人数为：15+9﹣20＝4．
故选：C．
【点评】本题考查既是党员又是大学生的志愿者人数的求法，考查集合中元素个数的判断等基础知识，考查运算求解能力，是基础题．
2．命题“有些梯形的对角线相等”的否定是（　　）
A．有些梯形的对角线不相等
B．所有梯形的对角线都相等
C．至少有一个梯形的对角线相等
D．没有一个梯形的对角线相等
【分析】根据含有量词的命题的否定即可得到结论．
【解答】解：特称命题的否定是全称量词命题，则命题“有些梯形的对角线相等”的否定是“没有一个梯形的对角线相等”，
故选：D．
【点评】本题主要考查含有量词的命题的否定，属于基础题．
3．已知幂函数f（x）＝（3m2﹣11）xm在（0，+∞）上单调递减，则f（4）＝（　　）
A．2 B．16 C． D．
【分析】由题意，利用幂函数的定义，用待定系数法求出函数的解析式，可得要求函数的值．
【解答】解：由题意得，3m2﹣11＝1，且m＜0，解得m＝﹣2，
所以f（x）＝x﹣2，故f（4）＝4﹣2＝，
故选：D．
【点评】本题主要考查幂函数的定义，用待定系数法求函数的解析式，求函数的值，属于基础题．
4．“α是第四象限角”是“是第二或第四象限角”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
【分析】利用分类讨论和象限角的定义得到充分性成立，利用举实例得到必要性不成立．
【解答】解：①若α是第四象限角，则270°+k•360°＜α＜360°+k•360°，k∈Z，
∴135°+k•180°＜＜180°+k•180°，k∈Z，
当k＝2m为偶数时，则135°+m•360°＜＜180°+m•360°，m∈Z，∴是第二象限角，
当k＝2m+1为奇数时，则315°+m•360°＜＜360°+m•360°，m∈Z，∴是第四象限角，
∴是第二或第四象限角，∴充分性成立，
②当＝﹣80°是第四象限角时，则α＝﹣160°是第三象限角，∴必要性不成立，
∴α是第四象限角是是第二或第四象限角的充分不必要条件．
故选：A．
【点评】本题考查了象限角的判断，充要条件的判定，属于中档题．
5．现有两个相互啮合的齿轮，大轮有64齿，小轮有24齿，当小轮转一周时，大轮转动的弧度是（　　）
A． B． C． D．
【分析】根据已知条件，结合大轮与小轮转过的弧长相等，即可求解．
【解答】解：当小轮转一周时，大轮转动周，
则大轮转动的弧度是．
故选：C．
【点评】本题主要考查弧长公式，属于基础题．
6．某灯具商店销售一种节能灯，每件进价10元，每月销售量y（单位：件）与销售价格x（单位：元）之间满足如下关系式：y＝﹣10x+500（20＜x≤40且x∈N）．则灯具商店每月的最大利润为（　　）
A．3000元 B．4000元 C．3800元 D．4200元
【分析】先建立二次函数模型，再由二次函数的性质求解最值．
【解答】解：设灯具商店每月的利润为z元，
则z＝（x﹣10）（﹣10x+500）＝﹣10（x﹣30）2+4000≤4000，
故选：B．
【点评】本题主要考查函数模型及其应用，二次函数最值的求解等知识，属于基础题．
7．函数的单调递增区间为（　　）
A．（11，+∞） B．（﹣∞，11） C．（23，+∞） D．（﹣∞，﹣1）
【分析】由对数式的真数大于0求得函数定义域，再求出内层函数二次函数的减区间，即可求得原函数的增区间．
【解答】解：由x2﹣22x﹣23＞0，得x＜﹣1或x＞23，
∴函数的定义域为{x|x＜﹣1或x＞23}，
∵函数单调递减，且函数t＝x2﹣22x﹣23在（﹣∞，﹣1）上单调递减，
函数在（﹣∞，﹣1）上单调递增．
故选：D．
【点评】本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．
8．已知x＞0，y＞0，且x+2y＝2，则的最小值为（　　）
A．24 B．25 C．26 D．27
【分析】根据题意可得+＝（+）（x+2y）＝（34++），从而即可利用基本不等式进行求解．
【解答】解：由题意，，
当且仅当，即，时等号成立．
故选：B．
【点评】本题考查基本不等式的应用，考查学生逻辑推理和运算求解的能力，属于基础题．
9．已知a＝0.590.61，b＝0.610.59，，则（　　）
A．a＜b＜c B．c＜a＜b C．c＜b＜a D．a＜c＜b
【分析】本题利用幂函数和指数函数性质可判断a，b，根根对数运算可判断c最小．
【解答】解：∵幂函数y＝xa，当a＞0时，在（0，+∞）单调递增，
故b＝0.610.59＞0.590.59，
又指数函数y＝ax，当0＜a＜1时，在R上单调递减，
故0.590.59＞a＝0.590.61＞0，即b＞a，
，
所以c＜a＜b．
故选：B．
【点评】本题考查幂函数、指数函数，对数相关知识，属于基础题．
10．已知，则＝（　　）
A． B． C． D．
【分析】利用二倍角公式进行化简即可．
【解答】解：因为，所以，，
所以＝．
故选：C．
【点评】本题考查三角恒等变换，考查学生的运算能力，属于中档题．
11．已知f（x）是定义在[﹣5，5]上的偶函数，当﹣5≤x≤0时，f（x）的图象如图所示，则不等式＜0的解集为（　　）

A．（﹣π，﹣2）∪（0，2）∪（π，5] B．（﹣π，﹣2）∪（π，5）
C．（﹣5，﹣2）∪（0，π）∪（π，5） D．（﹣5，﹣2）∪（π，5）
【分析】由已知结合偶函数的对称性可确定0≤x≤5时函数性质，然后结合分式不等式的求法可求．
【解答】解：因为f（x）是定义在[﹣5，5]上的偶函数，当﹣5≤x≤0时，f（x）单调递减，f（﹣2）＝0，
所以0≤x≤5时，函数单调递增，f（2）＝0，
所以f（x）＞0的解集[﹣5，﹣2）∪（2，5]，f（x）＜0的解集（﹣2，2），
当﹣5≤x≤5时，sinx＞0的解集[﹣5，﹣π）∪（0，π），sinx＜0时的解集（﹣π，0）∪（π，5]，
则不等式＜0可转化为或，
解得﹣π＜x＜﹣2或π＜x≤5或0＜x＜2．
故选：A．
【点评】本题主要考查了偶函数的对称性在求解不等式中的应用，体现了数形结合思想的应用，属于中档题．
12．已知奇函数f（x）的定义域为R，若f（x+1）为偶函数，且f（﹣1）＝5，则f（1）+f（2）+⋯+f（2021）＝（　　）
A．10 B．﹣10 C．﹣5 D．5
【分析】通过函数的奇偶性推出f（x）是周期为4的周期函数，再计算f（1），f（2），f（3），f（4）的值后，即可得解．
【解答】解：由题意得，f（x+1）＝f（﹣x+1）＝﹣f（x﹣1）①，
所以f（x﹣1）＝f（（x﹣2）+1）＝﹣f（x﹣2﹣1）＝﹣f（x﹣3）②，
由①②得，f（x+1）＝f（x﹣3），
所以f（x）的周期为4，
因为f（1）＝﹣f（﹣1）＝﹣5，f（2）＝﹣f（0）＝0，f（3）＝﹣f（1）＝5，f（4）＝f（0）＝0，
所以f（1）+f（2）+f（3）+f（4）＝0，
所以f（1）+f（2）+⋯+f（2021）＝505×0+f（2021）＝f（1）＝﹣5．
故选：C．
【点评】本题考查函数奇偶性与周期性的综合应用，通过函数的奇偶性推出函数的周期性是解题的关键，考查逻辑推理能力和运算能力，属于中档题．
二、填空题：本题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．
13．已知角θ的终边经过点，则＝　　．
【分析】由已知利用任意角的三角函数的定义以及诱导公式即可求解．
【解答】解：因为角θ的终边经过点，
所以sinθ＝＝﹣，
由题意得．
故答案为：．
【点评】本题考查了任意角的三角函数的定义以及诱导公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
14．函数的值域为 　[3，+∞）　．
【分析】先判断和x2﹣x+1的单调性，从而判断f（x）的单调性，进而求值域．
【解答】解：由2x﹣4≥0，得x≥2．
因为在[2，+∞）上单调递增，且x2﹣x+1在[2，+∞）上单调递增．
因为f（x）在[2，+∞）上单调递增．
所以f（x）min＝f（2）＝3．
故答案为：[3，+∞）．
【点评】本题主要考查利用函数的单调性求值域，属于基础题．
15．已知函数f（x）＝log2|x﹣1|，则不等式f（1﹣x）≤2的解集为 　[﹣4，0）∪（0，4]　．
【分析】直接求解不等式即可得到结论．
【解答】解：由f（1﹣x）＝log2|x|≤2，得0＜|x|≤4，解得﹣4≤x≤4且x≠0．
故答案为：[﹣4，0）∪（0，4]．
【点评】本题主要考查对数不等式的解法，考查计算能力，属于基础题．
16．已知，，则cos2α+cos2β＝　　．
【分析】通过已知角和所求角之间的关系，将所求角的三角函数值转化为已知角的三角函数值可解．
【解答】解：cos2α+cos2β＝cos[（α+β）+（α﹣β）]+cos[（α+β）﹣（α﹣β）]
＝cos（α+β）cos（α﹣β）﹣sin（α+β）sin（α﹣β）+cos（α+β）cos（α﹣β）+sin（α+β）sin（α﹣β）
＝．
故答案为：﹣．
【点评】本题考查了三角函数的求值，属于基础题．
三、解答题：本题共6小题，共70分解答应写出文字说明、证明过程或演算步骤．
17．（10分）求值：
（1）；
（2）．
【分析】（1）利用指数幂的运算法则求解即可．
（2）利用对数的运算法则求解即可．
【解答】解：（1）原式＝•+π﹣2﹣1＝3﹣π﹣3＝π．
（2）原式＝log5100﹣log54+•﹣3＝log525+6﹣3＝2+6﹣3＝5．
【点评】本题考查指数幂，对数的运算法则，属于基础题．
18．（12分）已知集合A＝{x|2a﹣2≤x≤a}，B＝{x|﹣3＜x＜1}．
（1）若a＝﹣2，求A∪（∁RB）；
（2）若A∩B＝A，求a的取值范围．
【分析】（1）由已知结合集合的并集集补集运算即可求解；
（2）由题意得A⊆B，然后结合集合的包含关系对A是否为空集进行分类讨论可求．
【解答】解：（1）由题意得A＝{x|﹣6≤x≤﹣2}，∁RB＝{x|x≥1或x≤﹣3}，
故A∪（∁RB）＝{x|x≥1或x≤﹣2}；
（2）由题意得A⊆B，
①当A＝∅时，2a﹣2＞a，得a＞2，符合题意；．
②当A≠∅时，，得．
故a的取值范围为．
【点评】本题主要考查了集合的交集，补集集并集运算，还考查了集合的包含关系的应用，属于中等题．
19．（12分）已知函数f（x）＝loga（x+2a）（a＞0且a≠1）的图象过点（3，2）．
（1）求a的值；
（2）若函数，求g（x）≥2的解集．
【分析】（1）根据对数函数过定点，建立方程进行求解即可．
（2）求出g（x）的表达式，根据不等式的解法进行求解即可．
【解答】解：（1）∵f（x）的图象过点（3，2）．
∴由题意得f（3）＝loga（3+2a）＝2，得a2＝2a+3，即a2﹣2a﹣3＝0，
解得a＝3或﹣1（舍去），故a＝3．
（2）当a＝3时，f（x）＝log3（x+6），
由题意得．
当x＜2时，g（x）＝x+1≥2，解得1≤x＜2；
当x≥2时，g（x）＝log3（x+6）≥2，解得x≥3．
故g（x）≥2的解集为[1，2）∪[3，+∞）．
【点评】本题主要考查对数函数的图像和性质，根据对数函数的图像和性质求出函数的解析式是解决本题的关键，是中档题．
20．（12分）若将函数图象上所有点的横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度，得到函数g（x）的图象．
（1）求g（x）图象的对称中心；
（2）若，求的值．
【分析】（1）由题意利用函数y＝Asin（ωx+φ）的图象变换可求函数解析式，利用余弦函数的对称性即可求解．
（2）由题意利用诱导公式，同角三角函数基本关系式可求，进而利用二倍角的正切公式即可求解．
【解答】解：（1）将函数图象上所有点的横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度，得到，
由（k∈Z），
得（k∈Z），
故g（x）图象的对称中心为（k∈Z）．
（2）由题意得，
所以．
故．
【点评】本题考查了函数y＝Asin（ωx+φ）的图象变换，余弦函数的对称性，诱导公式，同角三角函数基本关系式以及二倍角的正切公式的应用，考查了转化思想和函数思想的应用，属于中档题．
21．（12分）已知函数．
（1）判断f（x）的奇偶性并说明理由；
（2）若对任意t∈R，k∈R，f（t2﹣t）+f（m﹣2t）＜k2恒成立，求m的取值范围．
【分析】（1）利用函数的奇偶性定义判断；
（2）先转化为对任意t∈R，f（t2﹣t）+f（m﹣2t）＜0恒成立，再根据函数的奇偶性和单调性转化为t2﹣3t+m＞0，对任意t∈R恒成立求解．
【解答】解：（1）f（x）是奇函数，理由如下：
f（x）的定义域为R，
，
故f（x）是奇函数．
（2）对任意t∈R，k∈R，f（t2﹣t）+f（m﹣2t）＜k2恒成立，
等价于对任意t∈R，f（t2﹣t）+f（m﹣2t）＜0恒成立，
等价于对任意t∈R，f（t2﹣t）＜﹣f（m﹣2t）＝f（2t﹣m）成立，
因为，
所以f（x）单调递减，
故对任意t∈R，t2﹣t＞2t﹣m，
即t2﹣3t+m＞0，
所以Δ＝9﹣4m＜0，
解得，
故m的取值范围是．
【点评】本题考查了函数奇偶性的判断以及函数的恒成立问题，属于中档题．
22．（12分）已知函数f（x）＝sincos﹣sin2+sin（x+）+．
（1）将f（x）化为Asin（ωx+φ）（A＞0，ω＞0，）的形式；
（2）若函数g（x）＝a[f（x）]2﹣2f（x）+1在（）上有4个零点，求a的取值范围．
【分析】（1）由题意，利用三角恒等变换化简f（x）的解析式，可得结果．
（2）由题意，令t＝f（x）∈（0，2），则at2﹣2t+1＝0在（0，2）上有2个不同的解，再利用二次函数的性质，求得a的范围．
【解答】解：（1）函数f（x）＝sincos﹣sin2+sin（x+）+＝sinx﹣•+（sinx+cosx）+
＝sinx+cosx＝2sin（x+）．
（2）∵x+∈（﹣，π），∴sin（x+）∈（﹣，1]，∴f（x）∈（﹣1，2]．
而函数g（x）＝a[f（x）]2﹣2f（x）+1在（）上有4个零点，
∴f（x）∈（0，2）．
∴令t＝f（x）∈（0，2），则at2﹣2t+1＝0在（0，2）上有2个不同的解，
∴．
求得＜a＜1，即a的取值范围为（，1）．
【点评】本题主要考查三角恒等变换，正弦函数的图象和性质，二次函数的性质，属于中档题．