初中数学北师大版七年级下册4 整式的乘法完美版ppt课件

这是一份初中数学北师大版七年级下册4 整式的乘法完美版ppt课件，文件包含143多项式与多项式相乘pptx、143多项式乘多项式教学设计docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

② 再把所得的积相加。
2.如何进行单项式与多项式乘法的运算？
① 用单项式分别去乘多项式的每一项；
1.单项式乘以多项式的依据是 ;
3.单项式与多项式乘法运算时，要注意一些什么?
① 不能漏乘,即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
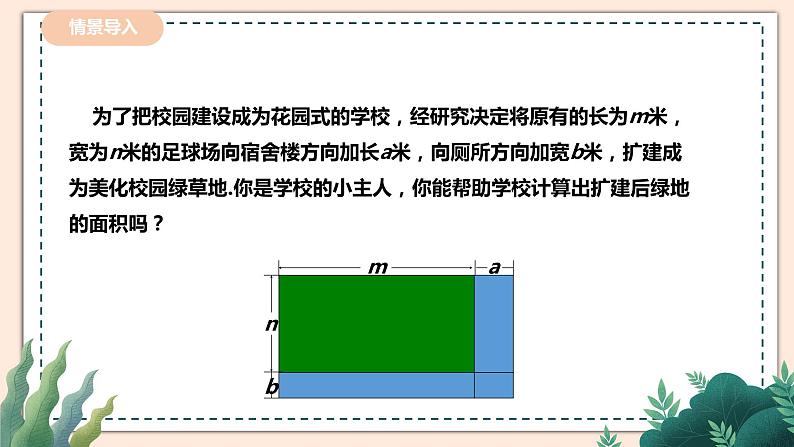
为了把校园建设成为花园式的学校，经研究决定将原有的长为m米，宽为n米的足球场向宿舍楼方向加长a米，向厕所方向加宽b米，扩建成为美化校园绿草地.你是学校的小主人，你能帮助学校计算出扩建后绿地的面积吗？
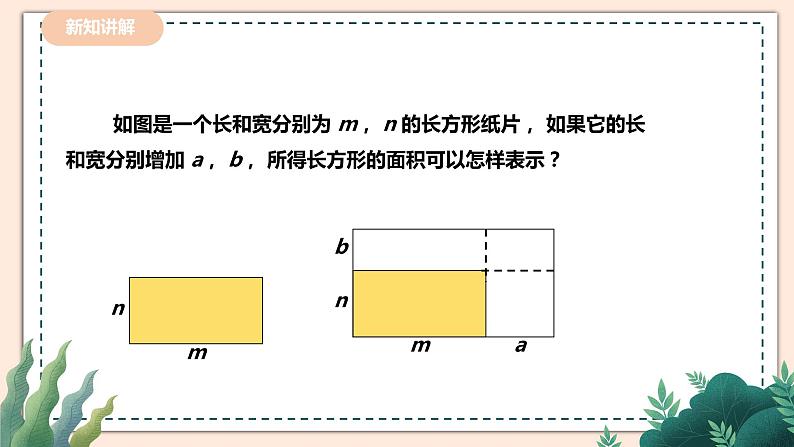
如图是一个长和宽分别为 m， n 的长方形纸片， 如果它的长和宽分别增加 a， b， 所得长方形的面积可以怎样表示？
小明的想法:长方形的面积可以有 4 种表示方式：( m+a ) (n+b )，n(m+a) +b(m+a)，m(n+b) + a(n+ b) 和mn+mb+na+ba，从而(m+a) (n+b) = n(m +a) + b(m+a) =m (n+b)+a (n+b) =mn+mb+na+ba．
你认为小明的想法对吗？从中你受到了什么启发？
把 (m+a) 或 (n+b) 看成一个整体，利用乘法分配律，可以得到 (m+a) (n+b) = (m+a)n+ (m+a)b =mn+an+mb+ab，或 ( m+a) (n+b)=m(n+b)+a( n+b) = mn+mb+an+ab．
如何进行多项式与多项式相乘的运算？
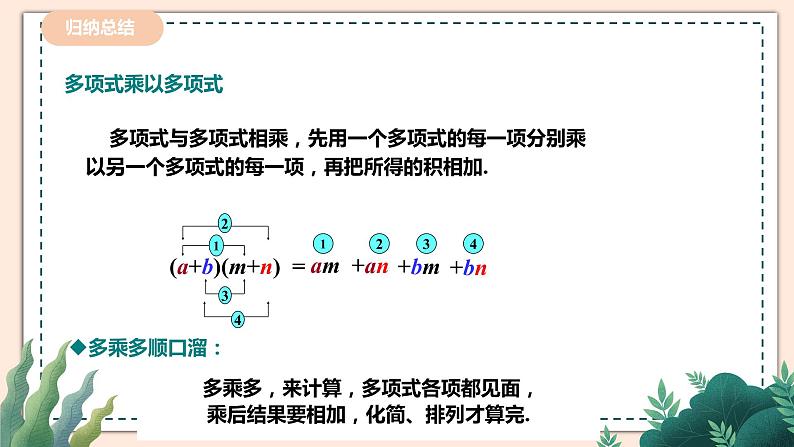
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
多乘多，来计算，多项式各项都见面，乘后结果要相加，化简、排列才算完.
（1） ( 1 – x ) ( 0.6 – x )； （2） ( 2x + y ) ( x – y )．
负负得正,一正一负得负。
1.两项相乘时，先定符号。
2.最后的结果要合并同类项.
所得积的符号由这两项的符号来确定：
3.运算要按一定顺序，做到不重不漏.4.多项式乘多项式，积的项数应等于两个多项式的项数之积.5.多项式的每一项分别与另一多项式的每一项相乘时，要带上每项前面的符号一起运算：同号相乘得正，异号相乘得负.
计算：(1) (4a-b)(-2b)2 ; (2)
解：(1) (4a-b)(-2b)2 = (4a-b)∙4b2 = 4a∙4b2+(-b)∙4b2 = 16ab2-4b3 ;
(1)多项式乘法法则的实质是将多项式与多项式相乘转化为几个单项式相乘的和的形式；(2) 多项式与多项式相乘的结果仍为多项式，若有同类项，一定要及时合并同类项，在合并同类项之前，积的项数应该是两个多项式的项数之积；(3)多项式乘法法则也适用于多个多项式相乘，即按顺序先将前两个多项式相乘，再把乘积与第三个多项式相乘，以此类推.
（x + 2）（x + 3）= x2 +____x +____
（x – 2）（x + 3）= x2 +____x +____
（x + 2）（x – 3）= x2 +____x +____
（x – 2）（x – 3）= x2 +____x +____
观察上面四个等式，你能发现什么规律？
多项式乘以多项式时，应注意以下几点：(1)相乘时，按一定的顺序进行，必须做到不重不漏；(2)多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积；(3)相乘后，若有同类项应该合并．
3.若(x＋4)(x－3)＝x2＋ax＋b，则a，b的值是(　　)A．a＝－1，b＝－12 B．a＝1，b＝－12C．a＝－1，b＝12 D．a＝1，b＝124.当x＝1时，ax＋b＋1的值为－2，则(a＋b－1)(1－a－b)的值为(　　)A．－16 B．－8 C．8 D．16
5.计算:(1)(3x+1)(x+2)； (2)(x-8y)(x-y)； (3) (x+y)(x2-xy+y2).
解： (1) 原式=3x·x+2·3x+1·x+1×2 =3x2+6x+x+2
(2) 原式=x·x-xy-8xy+8y2
=x2-9xy+8y2；
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2 =x3-x2y+xy2+x2y-xy2+y3 = x3+y3.
6.先化简，再求值：(x－2y)(x＋3y)－(2x－y)(x－4y)，其中x＝－1，y＝2.
原式＝x2＋3xy－2xy－6y2－(2x2－8xy－xy＋4y2) ＝x2＋xy－6y2－(2x2－9xy＋4y2) ＝x2＋xy－6y2－2x2＋9xy－4y2 ＝－x2＋10xy－10y2.当x＝－1，y＝2时，原式＝－(－1)2＋10×(－1)×2－10×22 ＝－1－20－40 ＝－61.
1.课本第19页习题1.8第1、2、3题
多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
不要漏乘；正确确定各项符号；结果要最简
实质上是转化为单项式×多项式的运算
(x－1)2=(x－1)(x－1)，而不是x2－12.