北师大版七年级下册6 完全平方公式完美版课件ppt

这是一份北师大版七年级下册6 完全平方公式完美版课件ppt，文件包含161完全平方公式pptx、161完全平方公式教学设计docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.
am+an+bm+bn
观察下列算式及其运算结果，你有什么发现？( m + 3 )2= ( m + 3 ) ( m + 3 ) = m 2 + 3m + 3m + 9= m 2 + 2×3m + 9 = m 2 + 6m + 9，
( 2 + 3 x ) 2 = ( 2 + 3x ) ( 2 +3 x ) = 22 + 2 ×3 x +2×3 x + 9 x2= 4 + 2×2×3 x + 9 x2 = 4 + 12 x + 9 x2 ．
填一填(1) (p+1)2= (p+1) (p+1) = .(2) (m+2)2 = .(3) (p－1)2 = (p－1) (p－1) = .(4) (m－2)2 = .
根据你发现的规律，你能写出下列式子的答案吗？
（a+b)2= .
（a-b)2= .
再举两例验证你的发现．
（1）（2x + y）2 ; （2）（3a – 2b）2 .
（1）（2x + y）2 =（2x + y）（2x + y） = 2x·2x + 2x·y + y·2x + y·y = 4x2 + 4xy + y2
（2）（3a – 2b）2 =（3a – 2b） （3a – 2b） = 3a·3a – 3a·2b – 2b·3a + 2b·2b = 9a2 – 12ab + 4b2
也就是说，两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.这两个公式叫做（乘法的）完全平方公式.
简记为：“首平方，尾平方，积的2倍放中间”
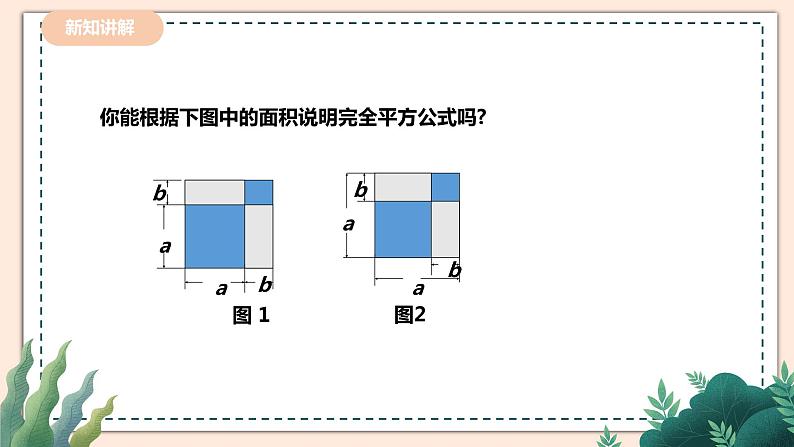
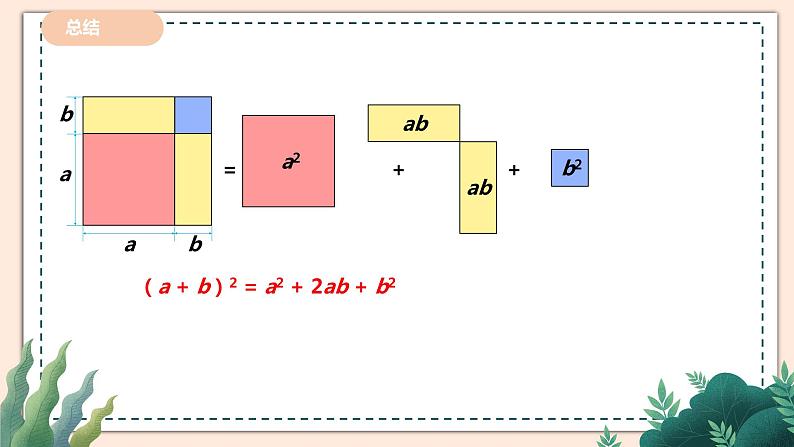
你能根据下图中的面积说明完全平方公式吗?
（a + b）2 = a2 + 2ab + b2
（a – b）2 = ？你是怎样做的？
（a – b）2 = a2 – 2ab + b2
(a+b)2= a2+2ab+b2.
(a-b)2=a2-2ab+b2.
观察下面两个完全平方式，比一比，回答下列问题：
1.说一说积的次数和项数.
2.两个完全平方式的积有相同的项吗？与a,b有什么关系？
3.两个完全平方式的积中不同的是哪一项？与a, b有什么关系？它的符号与什么有关？
4.公式中的字母a，b可以表示数，单项式和多项式.
2.积中两项为两数的平方和；
3.另一项是两数积的2倍，且与两数中间的符号相同.
例 1 利用完全平方公式计算：
（1）(2x – 3)2； （2）(4x + 5y)2； （3）(mn – a)2
解：（1） (2x – 3)2 = (2x)2 – 2·2x·3 + 32 = 4x2 – 12x + 9
（2）(4x + 5y )2 = (4x)2 + 2·4x·5y + (5y)2 = 16x2 + 40xy + 25y2
（3） (mn – a)2 = (mn)2 – 2·mn·a + a2 = m2n2 – 2amn + a2
运用完全平方公式计算：
（1） （4a-b)2
(3)(a+b+3)(a+b-3)
解：(a+b+3) (a+b−3)
=(a+b)2− 32
=a2 +2ab+b2－9
=[ (a+b) +3] [ (a+b) -3]
温馨提示：将(a+b)看作一个整体，解题中渗透了整体的思想
1．小萌在利用完全平方公式计算一个二项整式的平方时，得到正确结果4x2＋20xy＋ ，不小心把最后一项染黑了，你认为这一项是(　 　)A．5y2B．10y2C．100y2D．25y22．计算(x－2y)2的结果是(　 　)A．x2－4xy＋2y2B．x2－4xy＋4y2C．x2＋4xy＋4y2D．x2－4y2
3．计算：(1)(a＋b)2＝ 　 　 ；(2)(a－b)2＝ 　 　 ；(3)(5＋3p)2＝ 　 　 ；(4)(2x－7y)2＝ 　 　 ．
4．如图，最大正方形的面积可用两种形式表示：①　 　 　 ；② 　 　 ，这两个代数式表示同一块面积，由此得到完全平方公式③ 　 　 　 　 　 　 ．
5.计算(1)(3a＋b－2)(3a－b＋2)；(2)(x－y－m＋n)(x－y＋m－n)．
(2)原式=[(x-y)-(m-n)][(x-y)+(m-n)]
解：(1)原式=[3a＋(b－2)][3a－(b－2)]
=(3a)2－(b－2)2
=9a2-b2+4b-4.　
=(x-y)2-(m-n)2
=x2-2xy+y2-m2+2mn-n2.
6.已知x-y＝6，xy=-8.求: (1) x2+y2的值； (2)(x+y)2的值.
解：(1)因为x-y＝6，xy=-8，
(x-y)2＝x2+y2-2xy，
所以x2+y2＝(x-y)2+2xy
(2)因为x2+y2＝20，xy=-8，
所以(x+y)2＝x2+y2+2xy
1.课本第26页习题1.11第1、2、4题
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子，可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同（从公式结构特点及结果两方面）
a2+b2=(a+b)2-2ab=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.