北师大版七年级下册6 完全平方公式试讲课ppt课件

这是一份北师大版七年级下册6 完全平方公式试讲课ppt课件，文件包含162完全平方公式pptx、162完全平方公式教学设计docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

1.完全平方公式法则：
(a+b) 2=a2+2ab+b2
(a－b) 2=a2－2ab+b2
2. 想一想：（1）两个公式中的字母都能表示什么? （2）完全平方公式在计算化简中有些什么作用?
运用完全平方公式能使某些计算变得简便
想一想：103×97怎样用简便方法计算？
103×97=(100+3) (100－3)=1002－32=9 991 ；
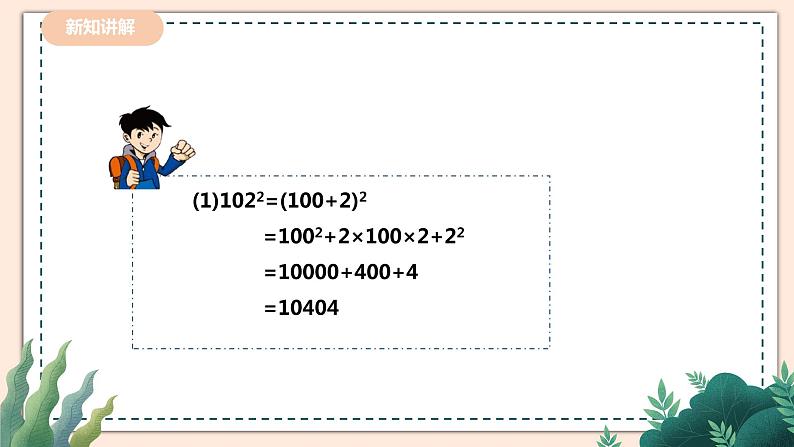
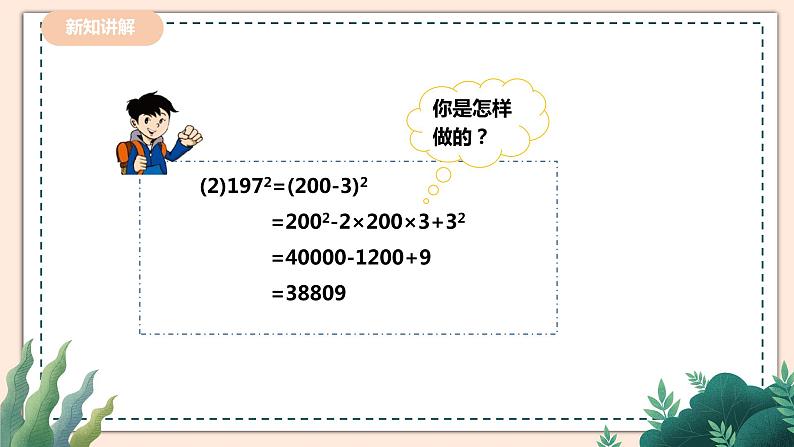
怎样计算1022，1972更简单呢？
能不能用公式进行简便计算？用哪个公式？
把 1022 改写成 (a+b)2 还是(a−b)2 的形式?
通过上面的计算，你发现了什么？
完全平方公式在用于简便运算的应用时，关键是找到与原数接近的整数，再将原数与整数进行比较，变形成(a+b)2 还是(a−b)2 的形式，使之符合公式的特点，再用完全平方公式进行求解．
例、计算：(1) (x+3)2－x2 ； (2) (a+b+3)(a+b－3)；(3) (x+5)2－(x－2) (x－3) .
(2) (a+b+3)(a+b－3)= [(a+b) +3] [(a+b)－3]= (a+b)2－32 =a2+2ab+b2－9；
解：(1) (x+3)2－x2= x2+6x+9－x2 =6x+9
(3) (x+5)2－(x－2) (x－3)= x2+10x+25－(x2－5x+6) = x2+10x+25－x2+5x－6= 15x+19 .
对于平方式中若底数是三项式，通过添括号将其中任意两项视为一个整体，就符合完全平方公式特点；对于两个三项式或四项式相乘的式子，可将相同的项及互为相反数的项分别添括号视为一个整体，转化成平方差公式的形式，通过平方差公式展开再利用完全平方公式展开，最后合并可得结果．
化简：(x－2y)(x2－4y2)(x＋2y).
解：原式=(x－2y)(x＋2y)(x2－4y2) =(x2－4y2)2 =x4－8x2y2＋16y4.
一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们.如果来1个孩子，老人就给这个孩子1块糖果，如果来2个孩子，老人就给每个孩子2块糖果，如果来3个孩子，老人就给每个孩子3块糖果……
(1) 第一天有a个孩子一起去看老人，老人一共给了这些孩子多少块糖？
(2) 第二天有b个孩子一起去看老人，老人一共给了这些孩子多少块糖？
(3)第三天有（a+b）个孩子一起去看老人，老人一共给了这些孩子多少块糖？
(4)这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？多多少？为什么？
因为(a+b)2-(a2+b2)=a2+2ab+b2-a2-b2=2ab
4．(x＋y－z)(x－y＋z)＝ 　 　 　 ．5．一个正方形的边长增加2 cm，它的面积就增加12 cm2，则这个正方形的边长是 ．
6.运用完全平方公式计算：(1) 962 ； (2) 2032 .
解：原式=（100－4）2=1002+42－2×100×4=10000+16－800=9216；
解：原式=（200+3）2=2002+32+2×200×3=40000+9+1200=41209.
7.已知x2+y2=8,x+y=4,求x－y.
解：∵x+y=4, ∴(x+y)2=16,即x2+y2+2xy=16①;
由①－②得2xy=8，②－得x2+y2－2xy=0.即(x－y)2=0，故x－y=0
1.课本第27页习题1.12第1、2、3、4题
在做题过程中一定要注意符号问题和正确认识a，b表示的意义，它们可以是数、也可以是单项式还可以是多项式，所以要记得添括号.
在解题之前应注意观察思考，选择不同的方法会有不同的效果，要学会优化选择.