初中北师大版1 两条直线的位置关系完整版课件ppt

这是一份初中北师大版1 两条直线的位置关系完整版课件ppt，文件包含211两条直线的位置关系pptx、211两条直线的位置关系教学设计docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
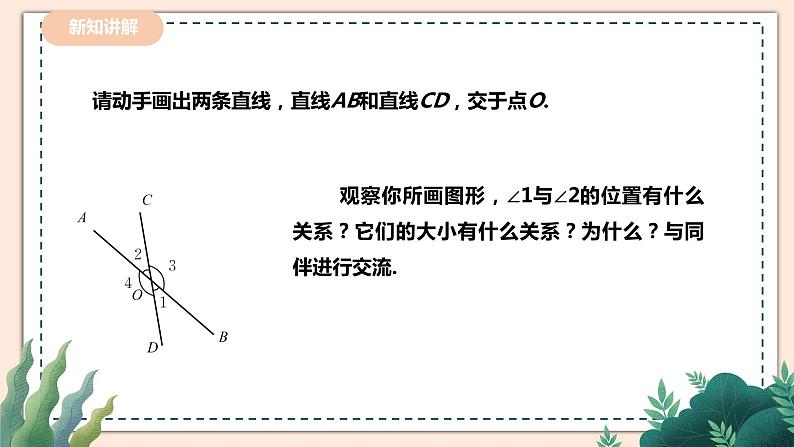
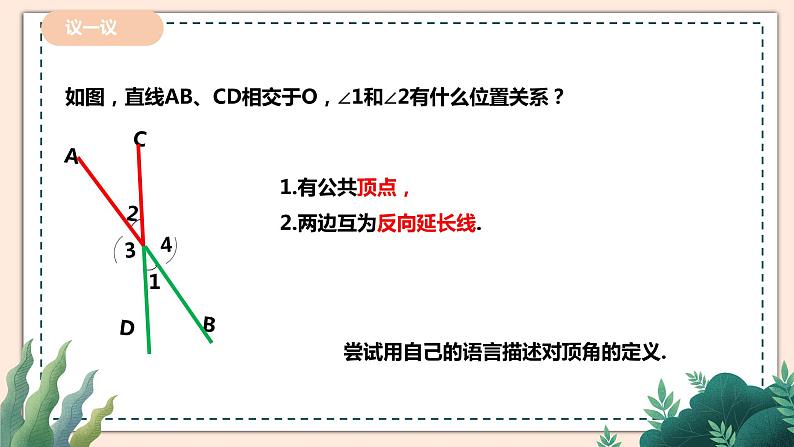
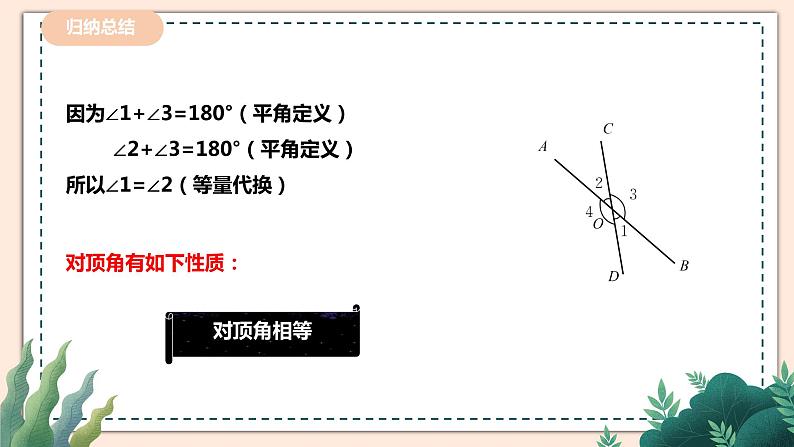
2.1.1两条直线的位置关系教学设计课题 两条直线的位置关系单元2学科数学年级七学习目标1、在具体的现实情境中，了解同一平面内两条直线的位置关系是平行和相交，理解对顶角、余角、补角等概念。2、探索并掌握对顶角相等、同角或等角的余角相等、同角或等角的补角相等的性质.重点余角、补角、对顶角的性质及其应用难点通过简单的推理，归纳出余角、补角的性质，并能用规范的语言描述性质 教学过程教学环节教师活动学生活动设计意图导入新课向同学们展示一些生活中的图片，让学生观察生活中的两条直线之间的位置关系。          生活中处处可见道路、房屋、山川、桥梁。在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。我们知道：在同一平面内，两条直线的位置关系有相交和平行两种.在同一平面内，不相交的两条直线叫平行线.    学生能通过观察、分析、归纳两直线的位置的关系  让学生感受生活与数学的联系：生活中处处可见道路、房屋、桥梁、楼梯…在大自然的杰作和人类的创造物中，蕴含着无数的相交线和平行线。讲授新课提问1：图中∠1与∠2的位置有什么关系？像∠1与∠2有公共顶点，两边互为反向延长线，具有这种位置关系的两个角叫做对顶角．提问2 ：∠1与∠2的大小有什么关系？为什么？∠1与∠2相等．提问3 ：你们能想办法验证一下吗？提问4 ：数学需要严谨的推理证明，那你能用数学推理的方法证明这两个角相等吗？因为∠COD=180°，所以∠1＋∠3=180°，所以∠1=180°－∠3；因为∠AOB=180°，所以∠2＋∠3=180°，所以∠2=180°－∠3；所以∠1=∠2由此我们可以得出对顶角的性质：对顶角相等．  提问1：在刚才我们所画的图形中，∠1与∠3有什么数量关系？∠1与∠3的和是180°．概念：如果两个角的和是180°，那么称这两个角互为补角．其中一角是另一个角的补角。即：∠1的补角是∠3；∠3的补角是∠1。那么在图形中还有哪些角是互为补角的？问题：（1）定义中的“互为”一词如何理解？（2）∠1 + ∠2 + ∠3 = 180°，能说∠1 、∠2、 ∠3 互补吗？（3）互补的两角是否一定有公共顶点或公共边？请同学们注意，互补是指两个角之间的数量关系，与它们的位置无关。类似地，如果两个角的和是900，那么称这两个角互为余角．比如:直角三角形中的两个锐角互余。  做一做如图1，打台球时，选择适当的方向用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图1简化成图2，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2.   小组合作交流，解决下列问题：在图2中问题1：哪些角互为余角？哪些角互为补角？问题2：∠3与∠4有什么关系？为什么？问题3：∠AOC与∠BOD有什么关系？为什么？   得出余角各补角的性质：同角或者等角的余角相等．同角或者等角的补角相等．     学生开始动手操作，有的同学开始用量角器测量，有的开始动手折叠．完成后让学生先在小组内交流，然后再在全班展示             学生自主完成，组内交流答案学生自主完成,小组内交流讨论，派代表展示           小组合作交流，归纳 让学生通过观察、操作、推理、交流等活动，使学生在自主学习的过程中，学会对顶角的概念及性质．同时利用学习过的有关事实解决问题，进一步巩固了对顶角的概念及其性质．        在相互补充、 相互学习中，体验“互补互余”仅仅表明了两个角的度量关系，并没有限 制角的位置关系；让学生在合作共赢中，更好地掌握新知识．同时掌握类比思想。    以学生感兴趣的体育新闻为情景，为学生提供了观察、操作、推理、等数学活动，使学生在自主学习的过程中，掌握“同角或者等角的补角相等．”“同角或者等角的余角相等．”并能够用自己的语言说出简单推理． 课堂练习1.如图，下列各组角中，是对顶角的一组是(　　)A．∠1和∠2    B．∠3和∠5C．∠3和∠4     D．∠1和∠52.下列说法正确的有(　　)①对顶角相等；②相等的角是对顶角；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不是对顶角，则这两个角不相等．A．1个　          B．2个　  C．3个　          D．4个3.下列说法中正确的是________．(填序号)①钝角与锐角互补；②∠α的余角是90°－∠α；③∠β的补角是180°－∠β；④若∠1＋∠2＋∠3＝90°，则∠1，∠2，∠3互余．4.①.因为∠1+∠2=90º，∠2+∠3=90º，所以∠1=____，理由是______________________.② 因为∠1+∠2=180º，∠2+∠3=180º，所以∠1=____，理由是______________________.5.如图，直线AB、CD相交于点O，OE平分∠AOB，OB平分∠DOF，若∠DOE=50°，求∠DOF的度数. 若一个角的补角等于它的余角的4 倍，求这个角的度数.         学生自主动手解决，老师进行订正。      及时练习巩固，体现学以致用的观念，消除学生学无所用的思想顾虑。课堂小结谈一谈这节课，你有哪些收获？教师与学生一起进行交流，共同回顾本节知识让学生与同伴交流获得结果，帮助他分析，找出问题原因，及时查漏补缺.板书2.1 两条直线的位置关系（1）1．两条直线的位置关系：相交和平行． 2．对顶角：性质：3．补角、余角定义： 4．性质：同角或者等角的余角相等同角或者等角的补角相等  板演区