






- 6.1 《感受可能性》 课件+教案 课件 15 次下载
- 6.2.1《频率的稳定性》 课件+教案 课件 18 次下载
- 6.3.1《简单概率的计算》 课件+教案 课件 17 次下载
- 6.3.2《判断游戏的公平性》 课件+教案 课件 15 次下载
- 6.3.3《计算与面积有关的事件的概率》 课件+教案 课件 16 次下载
数学七年级下册2 频率的稳定性精品课件ppt
展开北师版数学七年级下6.2.2频率的稳定性教案
课题 | 6.2.2频率的稳定性 | 单元 | 6 | 学科 | 数学 | 年级 | 七 |
学习 目标 | 1.经历猜测、试验、收集试验数据、分析试验结果等过程,体会数据的随机性. 2.通过试验让学生理解当试验次数较大时,试验频率稳定在某一常数附近,并据此估计出某一事件发生的频率. | ||||||
重点 | 通过试验让学生理解当试验次数较大时,试验的频率具有稳定性,并据此初步估计出某一事件发生的可能性大小. | ||||||
难点 | 大量重复试验得到频率的稳定值的分析. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
导入新课 | 结合图形完成下面问题. (1)明天会下雨是什么事件?可能性多大? (2)太阳从东方升起是什么事件?可能性大吗? (3)如果随机抛出一枚骰子,抛出的点数会是7吗?这是什么事件?可能性大吗? | 对生活中熟悉的事件的可能性做出直接的猜测和判断,教师不予评价,让学生自己省悟,从而对这节内容产生浓厚兴趣,激发学生学习热情. | 让学生体验数学来源于生活,既复习了之前所学习的知识,也为本节课知识的展开做好了铺垫. |
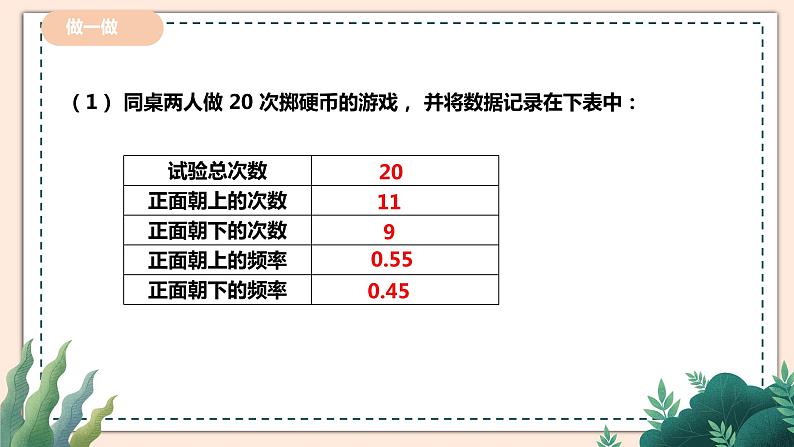
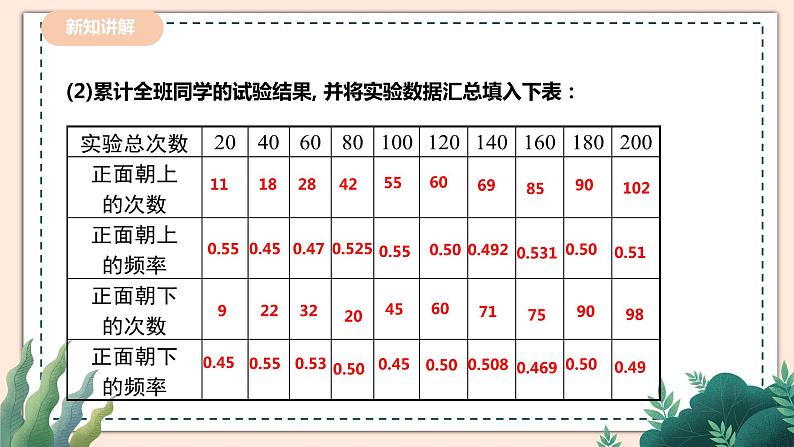
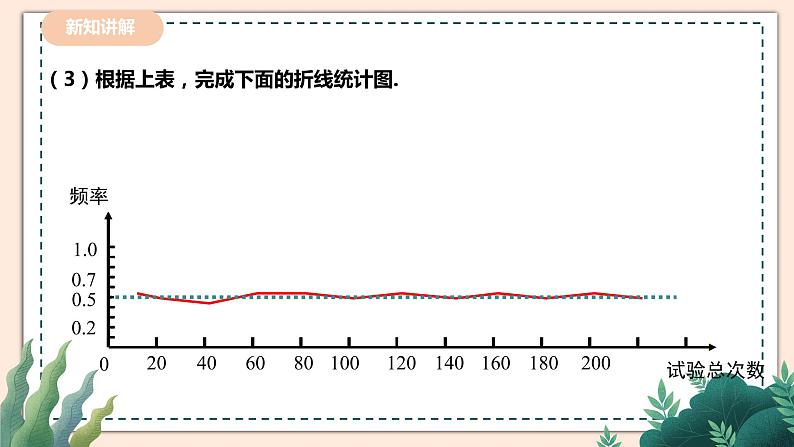
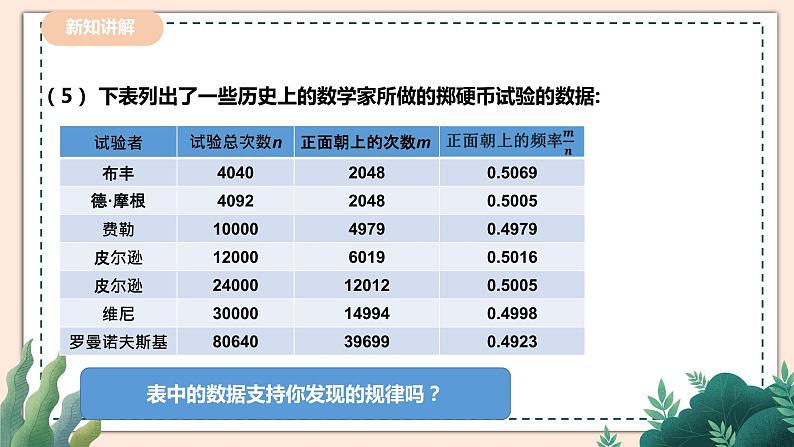
讲授新课 | 你认为一枚硬币抛出之后会怎么样?那么这几种情况哪种情况的可能性更大一些呢? 会出现正面或者反面。 出现正面或者反面的可能性应一样大。 让我们做实验来验证一下。 (1) 同桌两人做20次掷硬币的游戏,并将数据记录在下表中: (提示:硬币是均匀硬币,要从同一高度任意掷出) (2) 累计全班同学的试验结果,并将试验数据汇总填入下表: (3)根据上表,完成下面的折线统计图. (4)观察上面的折线统计图,你发现了什么规律? 当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小. 200个数据是不是太少了,能说明问题吗? 我们所做的试验不能说是大量的.但是有些人的确做了很多次. (5)表中的数据支持你发现的规律吗? 上表中正面出现的频率都接近0.5,这说明当抛硬币的次数足够多的时候,抛硬币正面和反面朝上的频率基本是一样的. 【总结归纳】 无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性. 由于事件A发生的频率表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P(A). 一般的,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率. 【想一想】 事件A发生的概率P(A)的取值范围是什么? 必然事件发生的概率是多少? 不可能事件发生的概率又是多少? 【总结归纳】 从定义可以得到二者的联系,可用大量重复试验中事件发生的频率来估计事件发生的概率.另一方面,大量重复试验中事件发生的频率稳定在某个常数(事件发生的概率)附近,说明概率是个定值,而频率随不同试验次数而有所不同,是概率的近似值,二者不能简单地等同.通过定义可以看出事件A发生的概率P(A)的取值范围是0≤P(A)≤1. 必然事件发生的概率为1; 不可能事件发生的概率为0; 随机事件A发生的概率P(A)是0与1之间的一个常数. 频率与概率的区别与联系. 1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率. 2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值. 【拓展提高】频率与概率的区别与联系. 1.联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率,因此可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率. 2.区别:某随机事件发生的概率是一个常数,是客观存在的,与试验次数无关.而频率是随机的,试验前无法确定.概率的统计定义是用频率表示的,但它又不同于频率的定义,只用频率来估计概率.频率是试验值,有不确定性,而概率是稳定值.
| 由掷硬币游戏培养学生猜测游戏结果的能力,并从中初步体会猜测事件发生的可能性.让学生体会猜测结果,这是很重要的一步,我们所学到的很多知识,都是先猜测,再经过多次的试验得出来的.由此引出猜测是需通过大量的试验来验证的.
通过掷硬币试验,发现在试验次数很少时,事件发生的频率不具有稳定性.可迅速吸引学生的注意力和调动学生探究问题的欲望,对接下来该如何验证问题得到结论,产生了思考,是继续试验更多的次数,还是……使学生树立在学习过程中找最佳解决办法的思想.
组讨论探讨,通过对事件发生的频率的分析来估计事件发生的概率,并掌握三类事件的概率值.
| 一是通过试验让学生体验等可能性事件发生的可能性的发现过程,二是培养学生的合作精神,通过试验和收集试验数据的过程使学生之间增进感情,并明白团队精神的重要性.
学生通过小组之间的合作、交流,用对不确定事件发生的频率的分析来估计事件发生的概率.再通过对历史上数学家所做掷硬币试验数据的讨论,学生的思维变得更加活跃,为回答接下来的新知应用做好准备.
突出本节课的重点,通过对事件发生的频率的分析来估计事件发生的概率,并掌握三类事件的概率值.
|
课堂练习 | 1.下列事件发生的可能性为0的是( ) A.掷两枚骰子,同时出现数字“6”朝上 B.小明从家里到学校用了10分钟,从学校回到家里却用了15分钟 C.今天是星期天,昨天必定是星期六 D.小明步行的速度是每小时50千米 2.小强练习射击,共射击1 000次,其中有670次击中靶子,由此可估计,小强射击一次击中靶子的概率是( ) A.33% B.60% C.67% D.1 3.做重复试验,抛掷一枚啤酒瓶盖1 000次,经过统计发现“凸面向上”的次数为420次,则由此可以估计抛掷这枚啤酒瓶盖出现“凸面向上”的概率为 . 4.有一箱规格相同的红、黄两种颜色的小塑料球共1 000个.为了估计这两种颜色的球各有多少个,小东将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为 . 5.小明学完了统计知识后,从“中国环境保护网”上查询到他所居住城市2009年全年的空气质量级别资料,用简单随机抽样的方法选取30天,并列出下表: 请你根据以上信息解答下面问题: (1)这次抽样中“空气质量不低于良”的频率为多少? (2)根据这次抽样的结果,请你估计2009年全年(共365天)空气质量为优的天数是多少?
|
学生自主完成习题,老师订正 |
让学生巩固已学知识,加深对知识的理解与运用 |
课堂小结 | 1.知识回顾. 2.谈谈这节课你有哪些收获? | 教师与学生一起进行交流,共同回顾本节知识 | 让学生与同伴交流获得结果,帮助他分析,找出问题原因,及时查漏补缺. |
板书 | 1.抛硬币试验 2.无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性. 3.必然事件发生的概率为1; 不可能事件发生的概率为0; 随机事件A发生的概率P(A)是0与1之间的一个常数. |
|
|
初中数学鲁教版 (五四制)七年级下册2 频率的稳定性完美版ppt课件: 这是一份初中数学鲁教版 (五四制)七年级下册2 频率的稳定性完美版ppt课件,文件包含922《频率的稳定性2》课件ppt、922《频率的稳定性2》教案doc等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学鲁教版 (五四制)七年级下册2 频率的稳定性精品课件ppt: 这是一份初中数学鲁教版 (五四制)七年级下册2 频率的稳定性精品课件ppt,文件包含921《频率的稳定性1》课件ppt、921《频率的稳定性1》教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中2 矩形的性质与判定完整版课件ppt: 这是一份初中2 矩形的性质与判定完整版课件ppt,文件包含622《矩形的性质与判定2》课件ppt、622《矩形的性质与判定2》教案doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。













