专题11 函数性质综合大题-【巅峰课堂】2022-2023学年高一数学热点题型归纳与分阶培优练（人教A版2019必修第一册）

这是一份专题11 函数性质综合大题-【巅峰课堂】2022-2023学年高一数学热点题型归纳与分阶培优练（人教A版2019必修第一册），文件包含专题11函数性质综合大题-巅峰课堂2022-2023学年高一数学热点题型归纳与分阶培优练人教A版2019必修第一册解析版docx、专题11函数性质综合大题-巅峰课堂2022-2023学年高一数学热点题型归纳与分阶培优练人教A版2019必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
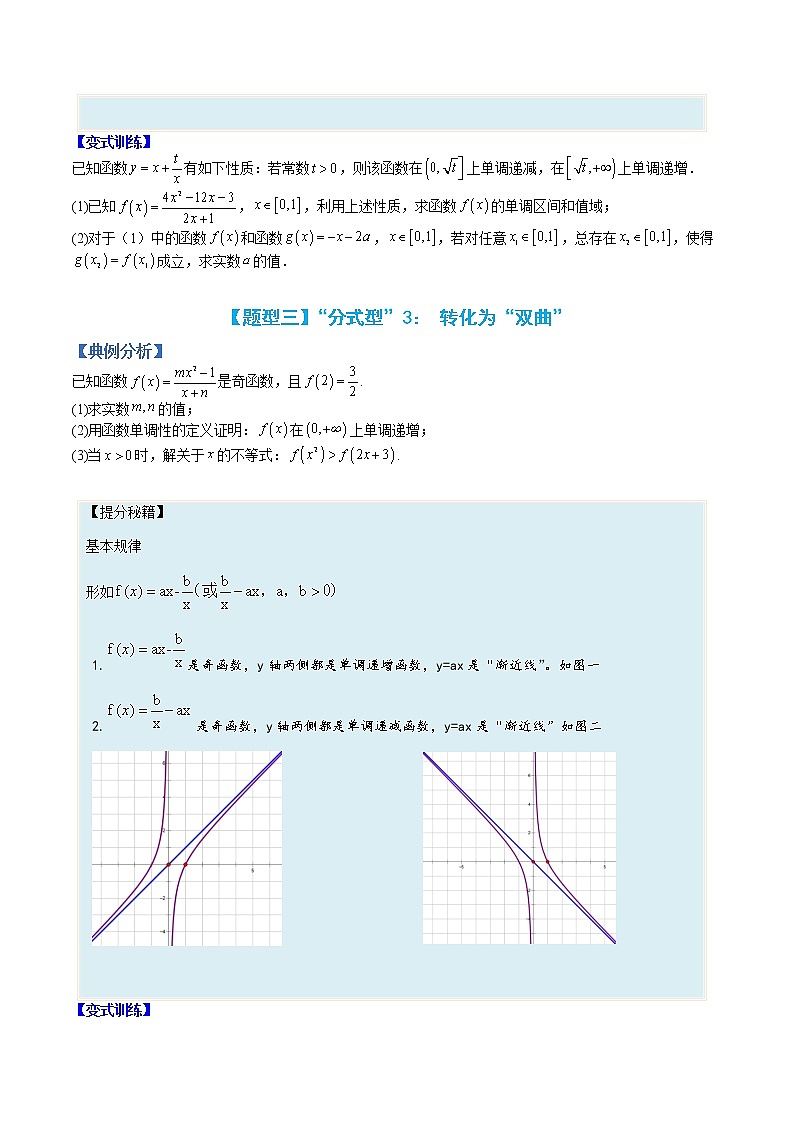
专题11 函数性质综合大题 目录【题型一】 “分式型”1：分离常数反比例函数【题型二】“分式型”2：转化为“对勾”...............................................2【题型三】“分式型”3： 转化为“双曲”..............................................3【题型四】“分式型”4：分母二次、分子一次型..........................................4【题型五】“分式型”5：分子、分母二次型..............................................5【题型六】“分式型”6：判别式法.....................................................5【题型七】“分式型”7：中心对称求和型...............................................6【题型八】“分式型”8：保值函数.....................................................6【题型九】分式型结构不良型.........................................................7【题型十】含绝对值型..............................................................8培优第一阶——基础过关练...........................................................8培优第二阶——能力提升练.............................................................9培优第三阶——培优拔尖练............................................................10    【题型一】 “分式型”1：分离常数反比例函数【典例分析】已知函数(常数).(1)若，在平面直角坐标系中画出该函数的图像;(2)若该函数在区间上是严格减函数，且在上存在自变量，使得函数值为正，求整数的值.  【提分秘籍】基本规律形如型1.通过分离常数，可以得到平移后反比例函数，在连续区间内，具有单调性，大题可用定义法证明，小题可用分离变量为主证明。在前两种方法掌握的前提下，可以适当引入快速画图法。2.反比例函数有对称中心，满足(其中（a，b）是对称中心，可通过“左加右减上加下减”求得.3.涉及到恒成立或者解不等式等问题，大多数可以转化为一元二次型求解。 【变式训练】已知函数，．(1)若，使得，求实数的取值范围；(2)若集合，对于都有，求实数的取值范围．  【题型二】“分式型”2：转化为“对勾” 【典例分析】  已知函数，，(1)当时，求函数的单调递增与单调递减区间（直接写出结果）；(2)当时，函数在区间上的最大值为，试求实数的取值范围；(3)若不等式对任意，（）恒成立，求实数的取值范围.  【提分秘籍】基本规律次型1.当b=0时分母是ax型。很容易出对勾或者双曲函数，可以用单调性（大题用定义法证明单调性）或者均值不等式搞定最值。2.当分母是ax-b型（b不为0），往往可以分离常数。对于理解力稍微好点的学生，还可以通过换元法（慎重，因为坐标系发生了变换）化简。程度差点的学生，可以换元化简后再还回去，也能达到分离常数的目的。 【变式训练】已知函数有如下性质：若常数，则该函数在上单调递减，在上单调递增．(1)已知，，利用上述性质，求函数的单调区间和值域；(2)对于（1）中的函数和函数，，若对任意，总存在，使得成立，求实数的值．  【题型三】“分式型”3： 转化为“双曲”【典例分析】已知函数是奇函数，且.(1)求实数的值；(2)用函数单调性的定义证明：在上单调递增；(3)当时，解关于的不等式：.  【提分秘籍】基本规律形如1.是奇函数，y轴两侧都是单调递增函数，y=ax是“渐近线”。如图一2.是奇函数，y轴两侧都是单调递减函数，y=ax是“渐近线”如图二                     【变式训练】已知函数满足.(1)求的解析式，并判断其奇偶性；(2)若对任意，不等式恒成立，求实数a的取值范围.  【题型四】“分式型”4：分母二次、分子一次型 【典例分析】已知函数是定义在上的奇函数，且.(1)求函数的解析式；(2)判断函数在上的单调性，并用定义证明；(3)解不等式：. 【提分秘籍】基本规律形如次型1.当b=0时分子是ax型时，可以在x≠0时，同时除x，分母得到对勾或者双刀函数，为小题做积累。2.当分子是ax-b时，也可以通过换元或者直接配凑，使得分母依旧是对勾或者双刀函数。3.大题中单调性证明，依旧是定义法 【变式训练】.已知函数是定义在上的奇函数，且.(1)求，的值；(2)判断在上的单调性，并用定义证明；(3)设，若对任意的，总存在，使得成立，求实数的取值范围. 【题型五】“分式型”5：分子、分母二次型 【典例分析】．已知．(1)若时，求的值域；(2)函数，若函数的值域为，求a的取值范围．  【提分秘籍】基本规律1.分子与分母都有二次型的，最常见的，就是分子分母可以分离常数达到降幂目的，有时候换元也可以。2.如果分母分子有线性关系，可以直接分离常数。这类题比较少。了解即可。3.必要时可以用判别式法。 【变式训练】求函数的单调区间，并比较与的大小．     【题型六】“分式型”6：判别式法【典例分析】已知函数．(1)解不等式：；(2)求函数的值域．   【变式训练】．已知函数．(1)求函数的值域；(2)若不等式在时恒成立，求实数k的最大值；  【题型七】“分式型”7：中心对称求和型 【典例分析】已知函数．(1)求，的值；(2)求证：的定值；(3)求的值． 【变式训练】已知函数.(1)求的值；(2)求证：是定值；(3)求的值.   【题型八】“分式型”8：保值函数 【典例分析】若函数在定义域的某个区间（）上的值域恰为（），则称函数为上的倍域函数，称函数的一个倍域区间．已知函数，且关于的不等式的解集为．(1)求实数，的值；(2)若（），是否存在（），使得函数为定义域内的某个区间上的倍域函数？若存在，请求出的值；若不存在，请说明理由．  【提分秘籍】基本规律把函数存在区间，使得函数为上的倍域函数，结合函数的单调性，转化为是解答的关键. 【变式训练】对于定义域为的函数，如果存在区间，使得在区间上是单调函数.且函数的值域是，则称区间是函数的一个“优美区间”(1)判断函数和函数是否存在“优美区间”？（直接写出结论，不要求证明）(2)如果是函数的一个“优美区间”，求的最大值；(3)如果函数在上存在“优美区间”，求实数的取值范围.  【题型九】分式型结构不良型 【典例分析】已知______，且函数.①函数在定义域上为偶函数；②函数在上的值域为.在①，②两个条件中，选择一个条件，将上面的题目补充完整，求出a，b的值，并解答本题.(1)判断的奇偶性，并证明你的结论；(2)设，对任意的R，总存在，使得成立，求实数c的取值范围.   【变式训练】已知函数，，从下面三个条件中任选一个条件，求出，的值，并解答后面的问题．（注：若选择多于一个，则按照第一个选择进行计分）①已知函数，满足；②已知函数在上的值域为；③已知函数，若在定义域上为偶函数．(1)判断在上的单调性；(2)解不等式．   【题型十】含绝对值型 【典例分析】已知函数是定义在上的偶函数，且.（1）求的值；（2）判断函数在区间上的单调性，并证明；（3）解不等式.  【提分秘籍】基本规律含绝对值型，以分类讨论为主要解题思想。 【变式训练】已知函数（1）写出函数的单调区间；（2）若在恒成立，求实数的取值范围；（3）若函数在上值域是，求实数的取值范围．   培优第一阶——基础过关练1.已知函数(1)判断的奇偶性；(2)若当时，恒成立，求实数的取值范围. 2．已知函数，函数为R上的奇函数，且.(1)求的解析式：(2)判断在区间上的单调性，并用定义给予证明：(3)若的定义域为时，求关于x的不等式的解集. 3．已知.(1)若函数是偶函数，且当时，，当时，求的表达式；(2)证明：函数在区间上是严格增函数. 4．已知函数.(1)判断的奇偶性，并证明；(2)证明：在区间上单调递减. 5．已知定义在上的函数.(1)求证：是奇函数；(2)求证：在上单调递增；(3)求不等式的解集.  培优第二阶——能力提升练1.已知函数是定义在上的奇函数，且．(1)求函数的解析式；(2)判断函数在上的单调性．(3)解关于t的不等式：．  2.已知函数（且）．(1)当的定义域为时，求函数的值域；(2)设函数，求的最小值． 3.已知函数．(1)用定义证明函数在区间上单调递增；(2)对任意都有成立，求实数的取值范围．  4.已知函数是奇函数，是偶函数.(1)求.(2)判断函数在上的单调性并说明理由，再求函数在上的最值.(3)若函数满足不等式，求出t的范围.  培优第三阶——培优拔尖练1.已知函数是奇函数，且．(1)求的解析式；(2)判断函数的单调性，并证明你的结论；(3)若，，且．求证． 2.已知函数是其定义域内的奇函数，且，(1)求的表达式；(2)设，求的值． 3.已知定义在上的函数为偶函数.(1)求的值；(2)判断在上的单调性（不用证明）；(3)已知函数，，若对，总有，使得成立，试求实数的取值范围. 4.设，.(1)若在区间上是单调函数，求a的取值范围；(2)若存在，使得对任意的，都有成立，求实数a的取值范围.