2021-2022学年山东省威海市乳山市鲁教版九年级（上）期末数学试卷（五四学制）(解析版)

这是一份2021-2022学年山东省威海市乳山市鲁教版九年级（上）期末数学试卷（五四学制）(解析版)，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年山东省威海市乳山市九年级（上）期末数学试卷（五四学制）
一、选择题（本大题共12小题，每小题3分，共36分．1-10题在每小题给出的四个选项中，只有一个是正确的，每小题选对得3分，选错、不选或多选，均不得分；11题和12题在每小题给出的四个选项中，错选、不选得0分，漏选得2分，全部选对得3分）
1．（3分）二次函数y＝（x﹣1）2+3的顶点坐标为（　　）
A．（1，3） B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）
2．（3分）随机抛掷两个均匀的骰子（六个面标记的数字分别是1，2，3，4，5，6），两个骰子点数之和是10的概率是（　　）
A． B． C． D．
3．（3分）如图，已知点P（4，3），OP与x轴正半轴的夹角为α，则cosα＝（　　）

A． B． C． D．
4．（3分）如图是将正方体切去一个角后的几何体，则该几何体的左视图是（　　）

A． B． C． D．
5．（3分）反比例函数y＝（x＜0）图象上有（x1，y1），（x2，y2）两点，已知y1＞y2，则x1与x2的大小关系是（　　）
A．x1＞x2 B．x1＜x2 C．x1＝x2 D．无法确定
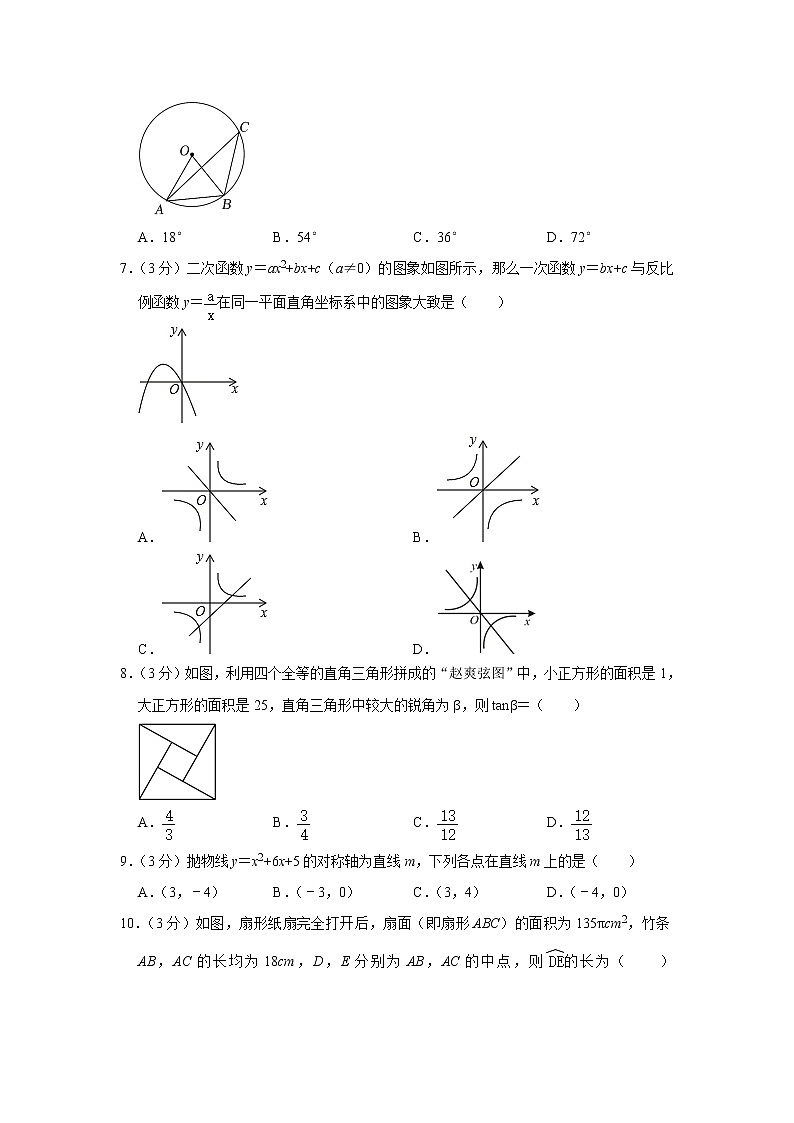
6．（3分）如图，点A，B，C都在⊙O上，若∠ACB＝36°，则∠OAB＝（　　）

A．18° B．54° C．36° D．72°
7．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么一次函数y＝bx+c与反比例函数y＝在同一平面直角坐标系中的图象大致是（　　）

A． B．
C． D．
8．（3分）如图，利用四个全等的直角三角形拼成的“赵爽弦图”中，小正方形的面积是1，大正方形的面积是25，直角三角形中较大的锐角为β，则tanβ＝（　　）

A． B． C． D．
9．（3分）抛物线y＝x2+6x+5的对称轴为直线m，下列各点在直线m上的是（　　）
A．（3，﹣4） B．（﹣3，0） C．（3，4） D．（﹣4，0）
10．（3分）如图，扇形纸扇完全打开后，扇面（即扇形ABC）的面积为135πcm2，竹条AB，AC的长均为18cm，D，E分别为AB，AC的中点，则的长为（　　）
A．cm B．7πcm C．cm D．8πcm
11．（3分）如图，在⊙O中，AB为直径，BC为切线，弦AD∥OC，直线CD交BA的延长线于点E，连接BD．下列结论不正确的是（　　）

A．CD是⊙O的切线 B．CO⊥DB
C．△EDA∽△EBD D．ED⋅BC＝2BO⋅BE
（多选）12．（3分）二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣3，0），对称轴为x＝﹣1．下列结论正确的是（　　）

A．abc＜0
B．2a﹣b＝0
C．4a+2b+c＜0
D．若（﹣5，y1），（2，y2）是抛物线上两点，则y1＞y2
二、填空题（本大题共6小题，每小题3分，共18分，只要求填出最后结果）
13．（3分）如图，AB为⊙O的弦，半径OD⊥AB于点C．若AB＝8，CD＝2，则⊙O的半径长为　 　．

14．（3分）已知蓄电池的电压为定值．使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，则蓄电池的电压是 　 　V．

15．（3分）如图，PA，PB与⊙O相切于A，B两点，点C在⊙O上，若∠C＝70°，则∠P＝　 　°．

16．（3分）在△ABC中，∠BAC＝120°，AB＝3，AC＝2，则tanB＝　 　．
17．（3分）将抛物线y＝3x2﹣2x﹣1绕顶点旋转180°，所得到的抛物线与y轴的交点坐标为 　 　．
18．（3分）如图，▱ABCD的顶点A在反比例函数y＝﹣的图象上，顶点B在x轴的正半轴上，顶点C和D在反比例函数y＝的图象上，且对角线AC∥x轴，则平行四边形ABCD的面积等于　 　．

三、解答题（本大题共7小题，共66分，写出必要的运算、推理过程）
19．（6分）计算：．
20．（8分）小依和小钟玩摸牌游戏，游戏规则：有3张正面分别标有数字1、2、3，且背面完全相同的纸牌，将纸牌洗匀后背面朝上放在桌面上，由小依随机抽出一张，记下牌面数字．放回后洗匀，再由小钟随机抽出一张，记下牌面数字．
（1）请用画树形图或列表的方法，表示出两次抽出的纸牌数字可能出现的所有结果；
（2）若规定：两次抽出的纸牌数字之和为奇数，则小依获胜；两次抽出的纸牌数字之和为偶数，则小钟获胜．这个游戏规则公平吗？为什么？

21．（9分）如图，一次函数y＝x+4的图象与反比例函数（k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．
（1）直接写出结果：k＝　 　，点B的坐标为 　 　；
（2）若点P在x轴上，且S△ACP＝3S△BOC，求点P的坐标．

22．（10分）某风景管理区，为提高旅游安全性，决定将到达景点步行台阶的倾角由45°改为30°，已知原台阶坡面AB长为5m（BC所在地面为水平面），调整后的台阶坡面为AD．求：

（1）调整后的台阶坡面会加长多少？
（2）调整后的台阶多占多长一段水平地面？（结果精确到0.1m，参考数据：，）

23．（10分）超市以每瓶12元的价格购进一批洗面奶，销售一段时间后，为了获得更多的利润，超市决定提高价格销售，若按每瓶20元的价格销售，每月能卖120瓶；若按每瓶25元的价格销售，每月能卖70瓶；已知每月销售瓶数y（瓶）是每瓶销售价格x（元）的一次函数．每瓶洗面奶的销售价格定为多少元时，能使该月获得最大利润？
24．（11分）如图，AB是⊙O的直径，C是圆上一点，弦CD⊥AB于点E，且DC＝AD．过点A作⊙O的切线，过点C作DA的平行线，两直线交于点F，FC的延长线交AB的延长线于点G．
（1）求证：FG与⊙O相切；
（2）连接EF，若AF＝2，求EF的长．

25．（12分）如图，抛物线y＝﹣x2+bx+c经过点A，B（1，0），点C在x轴上，∠ACB＝90°，OC＝2OB，tan∠ABC＝2．
（1）求抛物线的解析式；
（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使线段PE最大．
①求线段PE的最大值；
②在直线PD上存在点M，且点M在以AB为直径的圆上，求出点M的坐标．


2021-2022学年山东省威海市乳山市九年级（上）期末数学试卷（五四学制）
参考答案与试题解析
一、选择题（本大题共12小题，每小题3分，共36分．1-10题在每小题给出的四个选项中，只有一个是正确的，每小题选对得3分，选错、不选或多选，均不得分；11题和12题在每小题给出的四个选项中，错选、不选得0分，漏选得2分，全部选对得3分）
1．（3分）二次函数y＝（x﹣1）2+3的顶点坐标为（　　）
A．（1，3） B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）
【分析】由二次函数的顶点式可求得答案．
【解答】解：∵y＝（x﹣1）2+3，
∴抛物线顶点坐标为（1，3），
故选：A．
2．（3分）随机抛掷两个均匀的骰子（六个面标记的数字分别是1，2，3，4，5，6），两个骰子点数之和是10的概率是（　　）
A． B． C． D．
【分析】列表得出共有36种等可能的结果，其中两个骰子点数之和是10的结果有3种，再由概率公式求解即可．
【解答】解：列表如下：

1
2
3
4
5
6
1
（1，1）
（1，2）
（1，3）
（1，4）
（1，5）
（1，6）
2
（2，1）
（2，2）
（2，3）
（2，4）
（2，5）
（2，6）
3
（3，1）
（3，2）
（3，3）
（3，4）
（3，5）
（3，6）
4
（4，1）
（4，2）
（4，3）
（4，4）
（4，5）
（4，6）
5
（5，1）
（5，2）
（5，3）
（5，4）
（5，5）
（5，6）
6
（6，1）
（6，2）
（6，3）
（6，4）
（6，5）
（6，6）
共有36种等可能的结果，其中两个骰子点数之和是10的结果有3种，
∴两个骰子点数之和是10的概率为＝，
故选：C．
3．（3分）如图，已知点P（4，3），OP与x轴正半轴的夹角为α，则cosα＝（　　）

A． B． C． D．
【分析】过P作PN⊥x轴于N，PM⊥y轴于M，根据点P的坐标求出PN和ON，由勾股定理求出OP，由锐角三角函数的定义求出答案即可．
【解答】解：过P作PN⊥x轴于N，PM⊥y轴于M，则∠PMO＝∠PNO＝90°，

∵x轴⊥y轴，
∴∠MON＝∠PMO＝∠PNO＝90°，
∴四边形MONP是矩形，
∴PM＝ON，PN＝OM，
∵P（4，3），
∴ON＝PM＝4，PN＝3，
在Rt△PON中，由勾股定理得
OP＝，
∴，
故选：B．
4．（3分）如图是将正方体切去一个角后的几何体，则该几何体的左视图是（　　）

A． B． C． D．
【分析】根据从左边看得到的图形是左视图，可得答案．
【解答】解：从左边看是一个正方形的右上角部分是一个直角三角形，斜边是虚线，
故选：D．
5．（3分）反比例函数y＝（x＜0）图象上有（x1，y1），（x2，y2）两点，已知y1＞y2，则x1与x2的大小关系是（　　）
A．x1＞x2 B．x1＜x2 C．x1＝x2 D．无法确定
【分析】根据反比例函数系数k的正负结合反比例函数的性质得出反比例函数的单调性，再根据函数的单调性即可得出结论．
【解答】解：∵反比例函数y＝（x＜0）中k＝1＞0，
∴该反比例函数图象在x＜0中，y随着x的增大而减小，
∵y1＞y2，
∴x1＜x2，
故选：B．
6．（3分）如图，点A，B，C都在⊙O上，若∠ACB＝36°，则∠OAB＝（　　）

A．18° B．54° C．36° D．72°
【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半得到∠AOB，再用等腰三角形的性质即可得出结论．
【解答】解：∵∠ACB＝∠AOB，∠ACB＝36°，
∴∠AOB＝2×∠ACB＝72°．
∵OA＝OB，
∴△OAB是等腰三角形，
∵∠AOB+∠OAB+∠OBA＝180°，
∴∠OAB＝（180°﹣∠AOB）＝54°，
故选：B．
7．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么一次函数y＝bx+c与反比例函数y＝在同一平面直角坐标系中的图象大致是（　　）

A． B．
C． D．
【分析】先根据二次函数的图象开口向下可知a＜0，再由函数图象经过原点可知c＝0，利用排除法即可得出正确答案．
【解答】解：∵二次函数的图象开口向下，
∴反比例函数y＝的图象必在二、四象限，故A、C错误；
∵二次函数的图象经过原点，
∴c＝0，
∵对称轴在y轴左侧，
∴a、b符号相同，
∴b＜0，
∴y＝bx+c经过原点且呈下降趋势，
∴故B错误．
故选：D．
8．（3分）如图，利用四个全等的直角三角形拼成的“赵爽弦图”中，小正方形的面积是1，大正方形的面积是25，直角三角形中较大的锐角为β，则tanβ＝（　　）

A． B． C． D．
【分析】已知正方形的面积即可求出边长．根据勾股定理求出直角三角形的边长，即可求解．
【解答】解：由题意知，小正方形的边长为1，大正方形的边长为5．
设直角三角形中较小的边的边长为x，
则有（1+x）2+x2＝25．
解得x＝3（负值不合题意，舍去），
∴较长直角边为x+1＝4，
∴tanβ＝，
故选：A．
9．（3分）抛物线y＝x2+6x+5的对称轴为直线m，下列各点在直线m上的是（　　）
A．（3，﹣4） B．（﹣3，0） C．（3，4） D．（﹣4，0）
【分析】求出抛物线y＝x2+6x+5的对称轴直线m，即可判断出答案．
【解答】解：∵抛物线y＝x2+6x+5的对称轴为直线m＝﹣＝﹣3，
∴（﹣3，0）在直线m＝﹣3上．
故选：B．
10．（3分）如图，扇形纸扇完全打开后，扇面（即扇形ABC）的面积为135πcm2，竹条AB，AC的长均为18cm，D，E分别为AB，AC的中点，则的长为（　　）
A．cm B．7πcm C．cm D．8πcm
【分析】利用扇形的面积公式求出圆心角，可得结论．
【解答】解：设圆心角为n°．
则有＝135π，
∴n＝150°，
∴的长＝＝π，
故选：C．
11．（3分）如图，在⊙O中，AB为直径，BC为切线，弦AD∥OC，直线CD交BA的延长线于点E，连接BD．下列结论不正确的是（　　）

A．CD是⊙O的切线 B．CO⊥DB
C．△EDA∽△EBD D．ED⋅BC＝2BO⋅BE
【分析】由切线的性质得∠CBO＝90°，首先连接OD，易证得△COD≌△COB（SAS），然后由全等三角形的对应角相等，求得∠CDO＝90°，即可证得直线CD是⊙O的切线，故A正确；根据全等三角形的性质得到CD＝CB，根据线段垂直平分线的判定定理得到即CO⊥DB，故B正确；根据余角的性质得到∠ADE＝∠BDO，等量代换得到∠EDA＝∠DBE，根据相似三角形的判定定理得到△EDA∽△EBD，故C正确；根据相似三角形的性质得出ED•BC＝BO•BE，故D不正确．
【解答】解：连接DO．
∵AB为⊙O的直径，BC为⊙O的切线，
∴∠CBO＝90°，
∵AD∥OC，
∴∠DAO＝∠COB，∠ADO＝∠COD．
又∵OA＝OD，
∴∠DAO＝∠ADO，
∴∠COD＝∠COB．
在△COD和△COB中，
，
∴△COD≌△COB（SAS），
∴∠CDO＝∠CBO＝90°．
又∵点D在⊙O上，
∴CD是⊙O的切线；故A正确，
∵△COD≌△COB，
∴CD＝CB，
∵OD＝OB，
∴CO垂直平分DB，
即CO⊥DB，故B正确；
∵AB为⊙O的直径，DC为⊙O的切线，
∴∠EDO＝∠ADB＝90°，
∴∠EDA+∠ADO＝∠BDO+∠ADO＝90°，
∴∠ADE＝∠BDO，
∵OD＝OB，
∴∠ODB＝∠OBD，
∴∠EDA＝∠DBE，
∵∠E＝∠E，
∴△EDA∽△EBD，故C正确；
∵∠EDO＝∠EBC＝90°，
∠E＝∠E，
∴△EOD∽△ECB，
∴，
∵OD＝OB，
∴ED•BC＝BO•BE，故D错误；
故选：D．

（多选）12．（3分）二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣3，0），对称轴为x＝﹣1．下列结论正确的是（　　）

A．abc＜0
B．2a﹣b＝0
C．4a+2b+c＜0
D．若（﹣5，y1），（2，y2）是抛物线上两点，则y1＞y2
【分析】利用抛物线开口方向得到a＞0，利用对称轴方程得到b＝2a＞0，利用抛物线与y轴的交点位置得到c＜0，则可对A进行判断；利用b＝2a可对B进行判断；利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为（1，0），所以x＝2时，y＞0，则可对C进行判断；利用二次函数的性质对D进行判断．
【解答】解：A．∵抛物线开口向上，
∴a＞0，
∵抛物线的对称轴为直线x＝﹣＝﹣1，
∴b＝2a＞0，
∵抛物线与y轴的交点坐标在x轴下方，
∴c＜0，
∴abc＜0，
故选项正确，符合题意；
B．∵b＝2a，
∴2a﹣b＝0，
故选项正确，符合题意；
C．∵抛物线与x轴的一个交点坐标为（﹣3，0），对称轴为x＝﹣1，
∴抛物线与x轴的另一个交点坐标为（1，0），
∴当x＝2时，y＞0，
∴4a+2b+c＞0，
故选项错误，不符合题意；
D．∵点（﹣5，y1）到直线x＝﹣1的距离比点（2，y2）到直线x＝﹣1的距离大，
∴y1＞y2，
故选项正确，符合题意．
故选：ABD．
二、填空题（本大题共6小题，每小题3分，共18分，只要求填出最后结果）
13．（3分）如图，AB为⊙O的弦，半径OD⊥AB于点C．若AB＝8，CD＝2，则⊙O的半径长为　5　．

【分析】先根据垂径定理求出AC的长，设⊙O的半径为r，再连接OA，在Rt△OAC中利用勾股定理求出r的值即可．
【解答】解：∵⊙O的弦AB＝8，半径OD⊥AB，
∴AC＝AB＝×8＝4，
设⊙O的半径为r，则OC＝r﹣CD＝r﹣2，连接OA，
在Rt△OAC中，
OA2＝OC2+AC2，即r2＝（r﹣2）2+42，解得r＝5．
故答案为：5．
14．（3分）已知蓄电池的电压为定值．使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，则蓄电池的电压是 　36　V．

【分析】根据函数图象可用电阻R表示电流I的函数解析式为，其中U为电压，再把（4，9）代入可得U的值．
【解答】解：设用电阻R表示电流I的函数解析式为，
∵过（4，9），
∴U＝4×9＝36，
故答案为：36．
15．（3分）如图，PA，PB与⊙O相切于A，B两点，点C在⊙O上，若∠C＝70°，则∠P＝　40　°．

【分析】连接OA、OB，根据切线的性质得到∠PAO＝∠PBO＝90°，进而得到∠P＝180°﹣∠AOB，根据圆周角定理得出∠AOB＝2∠ACB，求出∠AOB的度数．
【解答】解：连接OA、OB，
∵PA、PB是⊙O切线，
∴PA⊥OA，PB⊥OB，
∴∠PAO＝∠PBO＝90°，
∵∠P+∠PAO+∠AOB+∠PBO＝360°，
∴∠P＝180°﹣∠AOB，
∵∠C＝70°，
∴∠AOB＝2∠C＝140°，
∴∠P＝180°﹣140°＝40°，
故答案为：40．

16．（3分）在△ABC中，∠BAC＝120°，AB＝3，AC＝2，则tanB＝　　．
【分析】过点C作CD⊥AB，根据∠BAC＝120°，∠DAC＝60°，由三角函数得出AD，CD，在Rt△BCD中，求∠B的正切即可．
【解答】解：过点C作CD⊥AB，交BA的延长线于点D，
∵∠BAC＝120°，
∴∠DAC＝180°﹣120°＝60°，
∴cos60°＝，sin60°＝，
∵AB＝3，AC＝2，
∴AD＝AC•cos60°＝2×＝1，
CD＝AC•sin60°＝2×＝，BD＝AD+AB＝1+3＝4，
在Rt△BCD中，tanB＝＝．
故答案为：．

17．（3分）将抛物线y＝3x2﹣2x﹣1绕顶点旋转180°，所得到的抛物线与y轴的交点坐标为 　（0，1）　．
【分析】先将原抛物线解析式化为顶点式，将其绕顶点旋转180°后，开口大小和顶点坐标都没有变化，变化的只是开口方向，可据此得出所求的结论．
【解答】解：y＝3x2﹣2x﹣1＝3（x﹣）2﹣，将原抛物线绕顶点旋转180°后，得y＝﹣3（x﹣）2+，
即：y＝﹣3x2+2x+1，
当x＝0时，y＝1，
所以新抛物线与y轴的交点坐标为（0，1）．
故答案为：（0，1）．
18．（3分）如图，▱ABCD的顶点A在反比例函数y＝﹣的图象上，顶点B在x轴的正半轴上，顶点C和D在反比例函数y＝的图象上，且对角线AC∥x轴，则平行四边形ABCD的面积等于　10　．

【分析】利用同底等高的三角形面积相等和比例系数k的几何意义求解．
【解答】解：连接OA、OC，记AC与y轴的交点为点E，
∵AC∥x轴，
∴AC⊥y轴，S△ABC＝S△AOC，
∴S△AOE＝＝1，S△ABC＝＝4，
∴S△AOC＝S△AOE+S△COE＝1+4＝5，
∴S△ABC＝5，
∵四边形ABCD是平行四边形，
∴S▱ABCD＝2S△ABC＝10．
故答案为：10．

三、解答题（本大题共7小题，共66分，写出必要的运算、推理过程）
19．（6分）计算：．
【分析】先计算特殊角的三角函数值，再计算乘法，最后计算加减．
【解答】解：
＝×﹣（）2+
＝3﹣×+1
＝3﹣+1
＝．
20．（8分）小依和小钟玩摸牌游戏，游戏规则：有3张正面分别标有数字1、2、3，且背面完全相同的纸牌，将纸牌洗匀后背面朝上放在桌面上，由小依随机抽出一张，记下牌面数字．放回后洗匀，再由小钟随机抽出一张，记下牌面数字．
（1）请用画树形图或列表的方法，表示出两次抽出的纸牌数字可能出现的所有结果；
（2）若规定：两次抽出的纸牌数字之和为奇数，则小依获胜；两次抽出的纸牌数字之和为偶数，则小钟获胜．这个游戏规则公平吗？为什么？

【分析】（1）根据题意直接列出树形图或列表即可；
（2）游戏是否公平，关键要看是否游戏双方各有50%赢的机会，本题中即两纸牌上的数字之和为偶数或奇数时的概率是否相等，求出概率比较，即可得出结论．
【解答】解：（1）列表法如下：

1
2
3
1
（1，1）
（1，2）
（1，3）
2
（2，1）
（2，2）
（2，3）
3
（3，1）
（3，2）
（3，3）
（2）不公平．
理由：因为两纸牌上的数字之和有以下几种情况：
1+1＝2；2+1＝3；3+1＝4；1+2＝3；2+2＝4；3+2＝5；1+3＝4；2+3＝5；3+3＝6共9种情况，
其中5个偶数，4个奇数．
即小依获胜的概率为，而小钟的概率为，
∴＞，
∴此游戏不公平．
21．（9分）如图，一次函数y＝x+4的图象与反比例函数（k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．
（1）直接写出结果：k＝　﹣3　，点B的坐标为 　（﹣3，1）　；
（2）若点P在x轴上，且S△ACP＝3S△BOC，求点P的坐标．

【分析】（1）利用点A在y＝﹣x+4上求a，进而代入反比例函数y＝求k，然后联立方程求出交点；
（2）设出点P坐标表示三角形面积，求出P点坐标．
【解答】解：（1）把点A（﹣1，a）代入y＝x+4，得a＝3，
∴A（﹣1，3）
把A（﹣1，3）代入反比例函数y＝，
∴k＝﹣3；
∴反比例函数的表达式为y＝﹣，
联立两个函数的表达式得，
解得或，
∴点B的坐标为B（﹣3，1）；
解答：﹣3，（﹣3，1）；
（2）当y＝x+4＝0时，得x＝﹣4，
∴点C（﹣4，0），
设点P的坐标为（x，0），
∵S△ACP＝3S△BOC，
∴×3×|x+4|＝3××4×1，
解得x1＝0，x2＝﹣8，
∴点P（0，0）或（﹣8，0）．
22．（10分）某风景管理区，为提高旅游安全性，决定将到达景点步行台阶的倾角由45°改为30°，已知原台阶坡面AB长为5m（BC所在地面为水平面），调整后的台阶坡面为AD．求：

（1）调整后的台阶坡面会加长多少？
（2）调整后的台阶多占多长一段水平地面？（结果精确到0.1m，参考数据：，）

【分析】（1）先解直角△ABC求出AC的长，再解直角△ADC求出AD的长即可得到答案；
（2）分别解直角三角形求出CD，BC的长即可得到答案．
【解答】解：（1）由题意得，∠ABC＝45°，∠ACB＝90°，∠ADC＝30°，
∴在Rt△ABC中，．
∴在Rt△ADC中，．
∴AD﹣AB＝5≈2.1（m）
答：调整后的台阶坡面会加长2.1m；
（2）在Rt△ADC中，CD＝＝（m）
在Rt△ABC中，BC＝AB•cos∠ABC＝（m）
∴BD＝CD﹣BC＝＝2.6（m）．
答：调整后的台阶多占水平地面2.6m．
23．（10分）超市以每瓶12元的价格购进一批洗面奶，销售一段时间后，为了获得更多的利润，超市决定提高价格销售，若按每瓶20元的价格销售，每月能卖120瓶；若按每瓶25元的价格销售，每月能卖70瓶；已知每月销售瓶数y（瓶）是每瓶销售价格x（元）的一次函数．每瓶洗面奶的销售价格定为多少元时，能使该月获得最大利润？
【分析】首先求出y与x的函数关系式，设每月的利润为P，构建二次函数，利用二次函数的性质即可解决问题．
【解答】解：设y与x的函数关系式为y＝kx+b，
由题意，解得，
∴y与x的函数关系式为y＝﹣10x+320．
设每月的利润为P，则P＝（﹣10x+320）x﹣（﹣10x+320）×12
＝﹣10x2+440x﹣3840，
∴x＝＝22时，利润最大，
∴销售价格定为每瓶22元时，该月获得利润最大．
24．（11分）如图，AB是⊙O的直径，C是圆上一点，弦CD⊥AB于点E，且DC＝AD．过点A作⊙O的切线，过点C作DA的平行线，两直线交于点F，FC的延长线交AB的延长线于点G．
（1）求证：FG与⊙O相切；
（2）连接EF，若AF＝2，求EF的长．

【分析】（1）方法一：连接OC，AC．易证△ACD为等边三角形，所以∠D＝∠DCA＝∠DAC＝60°，从而可知∠DCO＝∠DCA＝30°，由于FG∥DA，易知∠OCF＝∠DCF﹣∠DCO＝90°，所以FG与⊙O相切．
方法二：同方法一求出∠AOC＝120°，由平行线的性质得出∠G＝30°，由三角形外角的性质可得出答案；
（2）求出AG＝2，证明△ADE≌△GCE（AAS），求出AE＝，由勾股定理可求出EF的长．
【解答】解：（1）方法一：如图1，连接OC，AC．

∵AB是⊙O的直径，弦CD⊥AB于点E，
∴CE＝DE，AD＝AC．
∵DC＝AD，
∴DC＝AD＝AC．
∴△ACD为等边三角形．
∴∠D＝∠DCA＝∠DAC＝60°．
∴∠DCO＝∠DCA＝30°，
∵FG∥DA，
∴∠DCF+∠D＝180°．
∴∠DCF＝180°﹣∠D＝120°．
∴∠OCF＝∠DCF﹣∠DCO＝90°，
∴FG⊥OC．
∴FG与⊙O相切；
方法二：连接OC，

∵AB是⊙O的直径，弦CD⊥AB于点E，
∴CE＝DE，
∵DC＝AD，
∴AD＝2DE，
∴∠DAE＝30°，
∴∠D＝60°，
∴∠AOC＝120°，
∵FG∥AC，
∴∠G＝∠DAG＝30°，
∴∠GCO＝∠AOC﹣∠G＝120°﹣30°＝90°，
∴FG与⊙O相切；
（2）解：∵AF与⊙O相切，
∴AF⊥AG．
由(1)可知∠G＝30°,
∵AF＝2，
∴GF＝4,
∴AG＝2，
∵DE＝CE，∠DAE＝∠G，∠DEA＝∠CEG，
∴△ADE≌△GCE（AAS）．
∴AE＝GE＝，
∴EF＝＝．
25．（12分）如图，抛物线y＝﹣x2+bx+c经过点A，B（1，0），点C在x轴上，∠ACB＝90°，OC＝2OB，tan∠ABC＝2．
（1）求抛物线的解析式；
（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使线段PE最大．
①求线段PE的最大值；
②在直线PD上存在点M，且点M在以AB为直径的圆上，求出点M的坐标．

【分析】（1）解直角三角形求出AC，可得A（﹣2，6），再利用待定系数法求出b，c的值；
（2）①设P（a，﹣a2﹣3a+4），则E（a，﹣2a+2）．构建二次函数，利用二次函数的性质求解即可；
②设M ．利用勾股定理构建方程求解即可．
【解答】解：（1）∵B（1，0），
∴OB＝1，
∵OC＝2OB，
∴OC＝2，BC＝3，
∵∠ACB＝90°，tan∠ABC＝2，
∴＝2，
∴AC＝6，
∴A（﹣2，6），
把A（﹣2，6），B（1，0）代入y＝﹣x2+bx+c，得．
解得．
所以，抛物线的解析式为y＝﹣x2﹣3x+4．

（2）①∴A（﹣2，6），B（1，0），
∴AB的解析式为y＝﹣2x+2，
设P（a，﹣a2﹣3a+4），则E（a，﹣2a+2）．
∴PE＝﹣a2﹣a+2＝﹣（a+）2+，
∵﹣1＜0，
∴昂x＝﹣时，PE的值最大，最大值为．

②∵PE有最大值时，P．
由于点M在直线PD上，设M ．
可得：，，AB2＝32+62＝45，
∵点M在以AB为直径的圆上，
∴∠AMB＝90°．
∴AM2+BM2＝AB2，
∴+＝45，
解得，，．
所以，点M的坐标为或．