人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直同步达标检测题

这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直同步达标检测题，共6页。
A．垂直于同一直线的两条直线平行
B．垂直于同一直线的两条直线垂直
C．平行于同一平面的两条直线平行
D．垂直于同一平面的两条直线平行
2．(多选)若一条直线a与平面α垂直，下列平面中的两条直线与a垂直，可以保证直线与平面垂直的是( )
①四边形的两边 ②正六边形的两边
③圆的两条直径 ④三角形的两边
A．①② B．①③
C．②③ D．③④
3．已知四棱锥P ­ ABCD中，侧棱PA⊥平面ABCD，底面ABCD是矩形，则该四棱锥的4个侧面中直角三角形的个数是________．
4．在三棱锥V ­ ABC中，VA＝VC，AB＝BC，点D为AC的中点，求证：AC⊥平面VBD.
5.[2022·辽宁协作体高一期末]已知α，β，γ是三个不同的平面，l，m，n是三条不同的直线，且α∩β＝l，m，n⊂γ.在下列条件中，能推出l⊥γ的是( )
A．n⊥l，m⊥l B．m⊥l，n⊥α
C．n⊥α，m⊥α D．m⊥α，n⊥β
6．[2022·湖南张家界高一期末]《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马．已知在阳马P ­ ABCD中，侧棱PA⊥底面ABCD，且PA＝AB＝AD＝1，则直线PD与平面PAC所成角的正弦值等于( )
A． eq \f(1,2) B． eq \f(\r(3),3)
C． eq \f(\r(3),2) D． eq \f(\r(6),2)
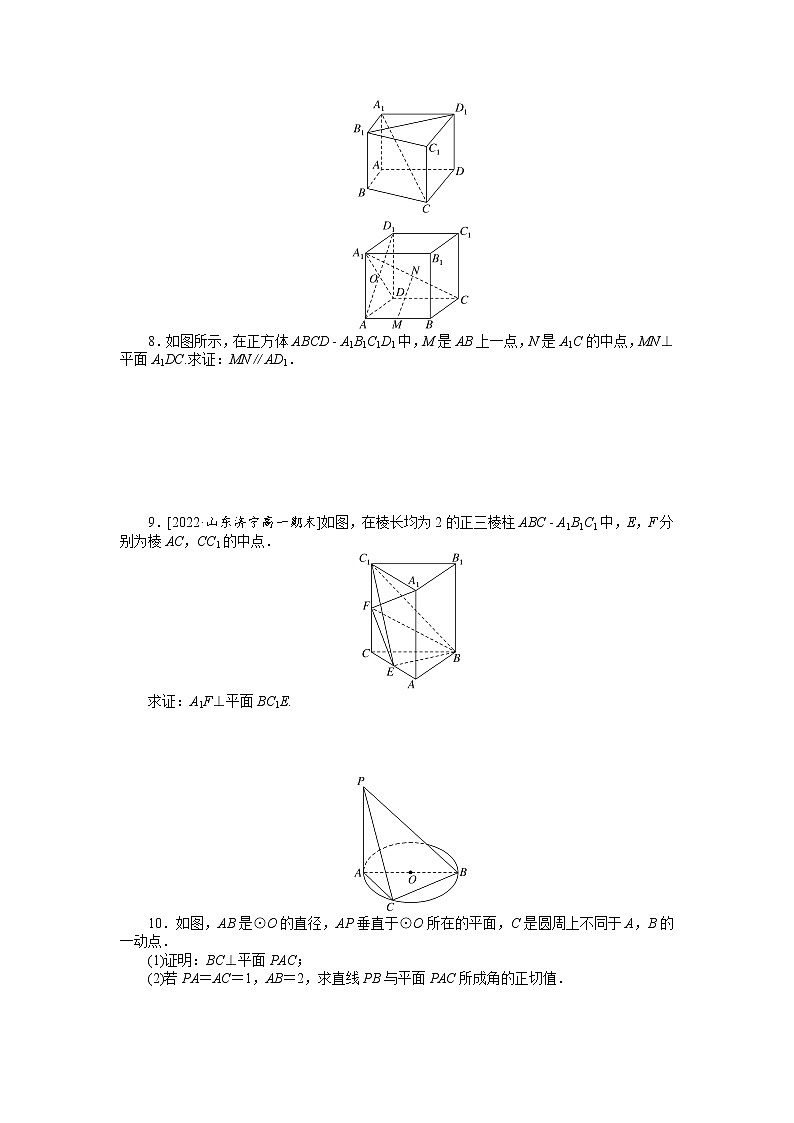
7．如图，在直四棱柱ABCD ­ A1B1C1D1中，当底面ABCD满足条件________时，有A1C⊥B1D1.(只需填写一种正确条件即可)
8．如图所示，在正方体ABCD ­ A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC.求证：MN∥AD1．
9．[2022·山东济宁高一期末]如图，在棱长均为2的正三棱柱ABC ­ A1B1C1中，E，F分别为棱AC，CC1的中点．
求证：A1F⊥平面BC1E.
10．如图，AB是⊙O的直径，AP垂直于⊙O所在的平面，C是圆周上不同于A，B的一动点．
(1)证明：BC⊥平面PAC；
(2)若PA＝AC＝1，AB＝2，求直线PB与平面PAC所成角的正切值．
11．[2022·湖北华中师大附中高一期末]如图，在三棱锥P ­ ABC中，PA⊥平面ABC，PA＝AB＝3，BC＝4，∠ABC＝90°，则点A到平面PBC的距离为( )
A． eq \f(3\r(2),2) B． eq \f(3,2)
C．3 D． eq \f(3\r(3),2)
12．[2022·山东烟台高一期末]如图，在四棱锥V ­ ABCD中，VA＝VD，BA＝BD.
(1)证明：AD⊥VB；
(2)在棱VC上是否存在一点P，使得VC⊥平面PAD？若存在，指出点P的位置；若不存在，说明理由．
答案：
1．解析：垂直于同一直线的两条直线的位置关系有：平行、相交和异面，A、B不正确；平行于同一平面的两条直线的位置关系有：平行、相交和异面，C不正确；根据线面垂直的性质可知：D正确．故选D.
答案：D
2．解析：对于①，四边形中的两条边可能平行，如平行四边形的对边，此时不能保证线面垂直；对于②，若直线垂直正六边形的两条平行的边，此时不能保证线面垂直；对于③，圆的两条直径交于圆心，故能保证线面垂直；对于④，三角形的任意两边一定相交，故能保证线面垂直．所以可以保证直线与平面垂直的是③④.故选D.
答案：D
3．解析：由题意，在四棱锥P ­ ABCD中，侧棱PA⊥平面ABCD，
可得PA⊥AD，PA⊥AB，
所以△PAD，△PAB为直角三角形；
又由四边形ABCD是矩形，所以AB⊥BC，
结合PA⊥BC，PA∩AB＝A，可得BC⊥平面PAB，
又因为PB⊂平面PAB，
所以BC⊥PB，所以△PBC为直角三角形，
同理，△PCD也为直角三角形，
该四棱锥的4个侧面中直角三角形的个数是4.
答案：4
4．解析：如图所示，连接VD，DB，
因为VA＝VC，AB＝BC，点D为AC的中点，
所以AC⊥VD，AC⊥BD，
又VD，BD是平面VBD内的两条相交直线，
所以AC⊥平面VBD.
5．解析：当m∥n时(如图所示)，由n⊥l，m⊥l推不出l⊥γ，即A错误；
同理可知，B，C错误；
若m⊥α，n⊥β，可知m与n交于一点，且n⊥l，m⊥l，所以l⊥γ，即D正确．故选D.
答案：D
6．解析：如图，在正方形ABCD中，连接BD交AC于O，则DO⊥AC，连接PO.因为PA⊥平面ABCD，DO⊂平面ABCD，所以PA⊥DO，而PO∩AC＝O，则DO⊥平面PAC，于是∠DPO是直线PD与平面PAC所成的角．
因为PA＝AD＝1，易知PA⊥AD，所以PD＝ eq \r(12＋12) ＝ eq \r(2) ，易得DO＝ eq \f(1,2) DB＝ eq \f(1,2) eq \r(12＋12) ＝ eq \f(\r(2),2) ，所以sin ∠DPO＝ eq \f(DO,PD) ＝ eq \f(1,2) ，即直线PD与平面PAC所成角的正弦值为 eq \f(1,2) .故选A.
答案：A
7．解析：根据直四棱柱ABCD ­ A1B1C1D1可得：BB1∥DD1，且BB1＝DD1，所以四边形BB1D1D是矩形，所以BD∥B1D1，同理可证：AC∥A1C1，当AC⊥BD时，可得：A1C1⊥B1D1，且CC1⊥底面A1B1C1D1，而B1D1⊂底面A1B1C1D1，所以CC1⊥B1D1，而A1C1∩CC1＝C1，从而B1D1⊥平面A1CC1，因为A1C⊂平面A1CC1，所以A1C⊥B1D1，所以当AC⊥BD时满足题意．
答案：AC⊥BD
8．证明：因为四边形ADD1A1为正方形，
所以AD1⊥A1D.
又因为CD⊥平面ADD1A1，
所以CD⊥AD1.
因为A1D∩CD＝D，
所以AD1⊥平面A1DC.
又因为MN⊥平面A1DC，所以MN∥AD1.
9．证明：由题意，AB＝BC，且E为棱AC的中点，故BE⊥AC，又正三棱柱ABC ­ A1B1C1，故CC1⊥平面ABC，
又BE⊂平面ABC，故BE⊥CC1，又AC∩CC1＝C，且AC，CC1⊂平面ACC1A1，故BE⊥平面ACC1A1.
因为A1F⊂平面ACC1A1，故BE⊥A1F.又tan ∠A1FC1＝ eq \f(A1C1,C1F) ＝2，tan ∠C1EC＝ eq \f(CC1,CE) ＝2，且∠A1FC1，∠C1EC均为锐角，故∠A1FC1＝∠C1EC.
又∠C1EC＋∠EC1C＝90°，故∠A1FC1＋∠EC1C＝90°，故A1F⊥C1E.
又C1E∩BE＝E，C1E，BE⊂平面BEC1，故A1F⊥平面BC1E.
10．解析：(1)证明：∵AB为圆O直径，
∴∠ACB＝90°即AC⊥BC.
∵PA⊥平面ABC，∴PA⊥BC.
∵AC∩PA＝A，
∴BC⊥平面PAC.
(2)∵BC⊥平面PAC，
∴∠BPC为PB与平面PAC所成的角，
在直角三角形ABC中，BC＝ eq \r(22－12) ＝ eq \r(3) ，
在直角三角形PAC中，PC＝ eq \r(12＋12) ＝ eq \r(2) ，
在直角三角形PBC中，tan ∠BPC＝ eq \f(\r(3),\r(2)) ＝ eq \f(\r(6),2) .
故直线PB与平面PAC所成角的正切值为 eq \f(\r(6),2) .
11．解析：因为PA⊥平面ABC，BC⊂平面ABC，所以PA⊥BC，
又因为∠ABC＝90°，即AB⊥BC，
因为PA∩AB＝A，所以BC⊥平面PAB，
又PB⊂平面PAB，所以BC⊥PB，
因为PA＝AB＝3，BC＝4，所以PB＝ eq \r(PA2＋AB2) ＝3 eq \r(2) ，
△PBC的面积S△PBC＝ eq \f(1,2) PB·BC＝6 eq \r(2) ，
设点A到平面PBC的距离为h，
则三棱锥P ­ ABC的体积V＝ eq \f(1,3) S△PBC·h＝ eq \f(1,3) S△ABC·PA，
即 eq \f(1,3) ×6 eq \r(2) h＝ eq \f(1,3) × eq \f(1,2) ×3×4×3，解得h＝ eq \f(3\r(2),2) ，
即点A到平面PBC的距离为 eq \f(3\r(2),2) .故选A.
答案：A
12．解析：(1)证明：取AD中点E，连接EV，EB.因为VA＝VD，所以AD⊥VE.
因为BA＝BD，所以AD⊥EB.又VE∩EB＝E，所以AD⊥平面VEB.
因为VB⊂平面VEB，所以AD⊥VB.
(2)假设在棱VC上存在一点P，使得VC⊥平面PAD.因为AD⊂平面PAD，所以AD⊥VC.
又AD⊥VB，VB∩VC＝V，所以AD⊥平面VBC.因为BC⊂平面VBC，所以AD⊥BC.
在平面ABCD中，因为AD⊥EB，AD⊥BC，所以EB∥BC，与EB∩BC＝B矛盾．
所以在棱VC上不存在点P，使得VC⊥平面PAD.