北师大版八年级下册2 直角三角形公开课ppt课件

这是一份北师大版八年级下册2 直角三角形公开课ppt课件，共32页。PPT课件主要包含了不一定全等，完全适用，全等AAS，全等AAS或ASA，全等SAS，做一做，画图思路，4连接A′B′，怎样证明你的结论，勾股定理等内容，欢迎下载使用。
（2）两边分别相等且其中一组等边的对角分别相等的两个三 角形全等吗？
（3）如果其中一组等边所对的角是直角呢？
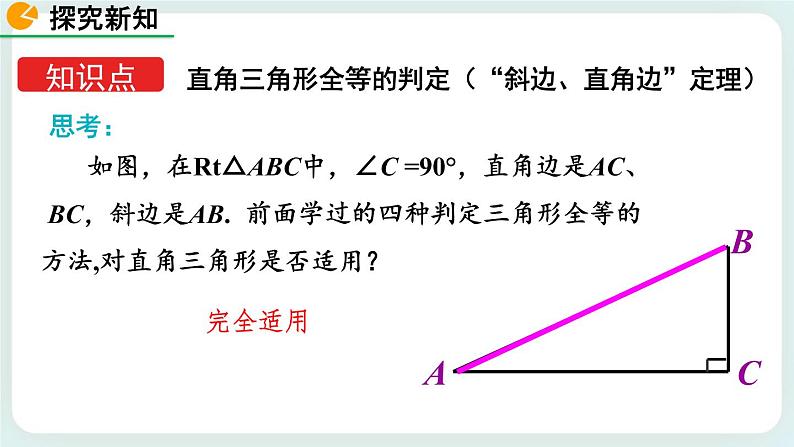
思考：（1）我们学过的判定三角形全等的方法？
SSS、 SAS、 ASA 、AAS.
这节课我们一起来探索并证明直角三角形全等的判定.
1. 探索并理解直角三角形全等的判定方法“HL”.
2. 会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
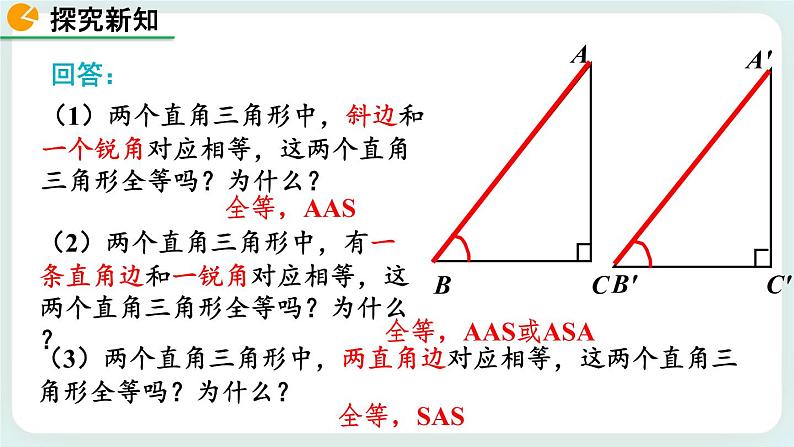
（1）两个直角三角形中，斜边和一个锐角对应相等，这两个直角三角形全等吗？为什么？
（2）两个直角三角形中，有一条直角边和一锐角对应相等，这两个直角三角形全等吗？为什么？
（3）两个直角三角形中，两直角边对应相等，这两个直角三角形全等吗？为什么？
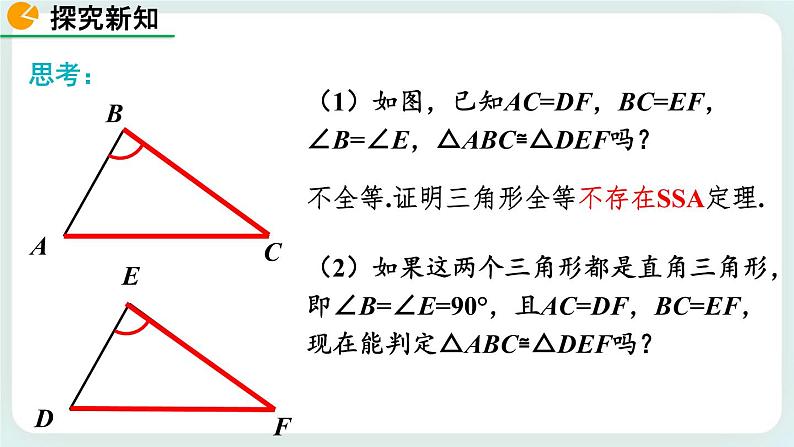
（1）如图，已知AC=DF，BC=EF，∠B=∠E，△ABC≌△DEF吗？
不全等.证明三角形全等不存在SSA定理.
（2）如果这两个三角形都是直角三角形，即∠B=∠E=90°，且AC=DF，BC=EF，现在能判定△ABC≌△DEF吗？
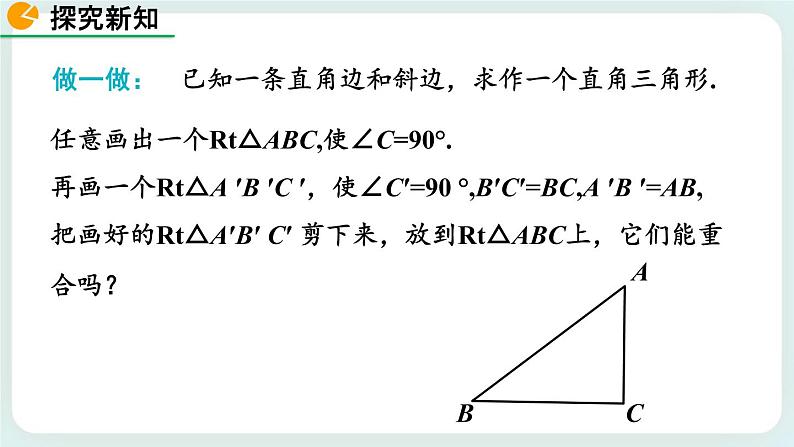
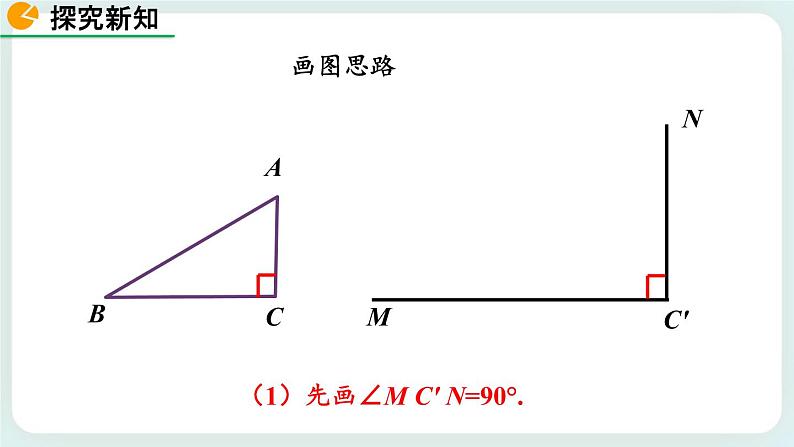
已知一条直角边和斜边，求作一个直角三角形.
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′，使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来，放到Rt△ABC上，它们能重合吗？
（1）先画∠M C′ N=90°.
（2）在射线C′M上截取B′C′=BC.
（3）以点B′为圆心，AB为半径画弧，交射线C′N于A′
思考：通过上面的探究，你能得出什么结论？
已知：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，AB=A′B′，BC=B′C′.求证：Rt△ABC≌Rt△A′B′C′.
证明:在Rt△ABC中,∵∠C=90°,∴AC2=AB2-BC2(______________). 同理,A′C′2=A′B′2-B′C′2(_____________). ∵AB=A′B′,BC=B′C′,∴AC=A′C′.∴Rt△ABC≌Rt△A′B′C′(_____). 
文字语言： 斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）.
“斜边、直角边”判定方法
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
在Rt△ABC 和 Rt△ A′B′C′ 中，
如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠B和∠F的大小有什么关系？
解：在Rt△ABC和Rt△DEF中,
∴ Rt△ABC≌Rt△DEF (HL).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
直角三角形全等的判定（“斜边、直角边”定理）
如图，两根长度均为12m的绳子，一端系在旗杆上，另一端分别固定在地面的两个木桩上，两个木桩离旗杆底部的距离相等吗?请说明你的理由.
解:∵AD⊥BC，∴∠ADB=∠ADC=90°，在Rt△ABD和Rt △ACD中,∴Rt△ABD≌Rt △ACD（HL），∴BD=CD.
例2 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4,则下列各图中的直角三角形与Rt△ABC全等的是 (　 　)
判断满足下列条件的两个直角三角形是否全等，不全等的画“×”，全等的注明理由： （1）一个锐角和这个角的对边对应相等；（ ） （2）一个锐角和这个角的邻边对应相等；（ ） （3）一个锐角和斜边对应相等； （ ） （4）两直角边对应相等； （ ） （5）一条直角边和斜边对应相等． （ ）
例3 如图，AC⊥BC， BD⊥AD， AC﹦BD，求证：BC﹦AD.
证明： ∵ AC⊥BC， BD⊥AD， ∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中，
∴ Rt△ABC≌Rt△BAD (HL).∴ BC﹦AD.

如图， ∠ACB =∠ADB=90°，要证明△ABC≌ △BAD，还需一个什么条件？把这些条件都写出来，并在相应的括号内填写出判定它们全等的理由. （1） （ ） （2） （ ） （3） （ ） （4） （ ）
∠ DAB= ∠ CBA
∠ DBA= ∠ CAB
如图，AC、BD相交于点P,AC⊥BC，BD⊥AD，垂足分别为C、D,AD=BC.求证：AC=BD.
Rt△ABD≌Rt△BAC
如图：AB⊥AD，CD⊥BC，AB=CD,判断AD和BC的位置关系.
Rt△ABD≌Rt△CDB
（2020·黑龙江）如图，Rt△ABC和Rt△EDF中，∠B=∠D，在不添加任何辅助线的情况下，请你添加一个条件 ，使Rt△ABC和Rt△EDF全等.
AB=ED(BC=DF或AC=EF或AE=CF)
1. 如图,MN∥PQ,AB⊥PQ,点A,D,B,C分别在直线MN和PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=______.
照此修改后面几页的课堂检测
2. 如图,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是(　 　)A.90° B.60° C.30° D.15°
3. 判断两个直角三角形全等的方法不正确的有（ ） A.两条直角边对应相等 B.斜边和一锐角对应相等 C.斜边和一条直角边对应相等 D.两个锐角对应相等
4.如图，在△ABC中，AB＝AC，AD⊥BD，AE⊥CE，垂足分别为D、E，且AD＝AE，BD、CE交于点O.求证：OB＝OC.
证明：∵AD⊥BD，AE⊥CE，∴∠D＝∠E＝90°.在Rt△ABD和Rt△ACE中，∵AB＝AC，AD＝AE，∴Rt△ABD≌Rt△ACE（HL），∴∠ABD＝∠ACE，∵AB＝AC，∴∠ABC＝∠ACB，∴∠ABC－∠ABD＝∠ACB－∠ACE，即∠OBC＝∠OCB，∴OB＝OC.
5.如图，AC⊥BC，AD⊥BD，AD＝BC，CE⊥AB，DF⊥AB，垂足分别是E、F.求证：CE＝DF.
证明： ∵AC⊥BC，AD⊥BD，∴在Rt△ABC和Rt△BAD中，AB＝AB,BC＝AD，∴Rt△ABC≌Rt△BAD（HL），∴∠DAF＝∠CBE.在△BCE和△ADF中，∠CEB＝∠DFA＝90°，∠CBE＝∠DAF,BC＝AD，∴△BCE≌△ADF（AAS），∴CE＝DF.
解:AE⊥BF,理由如下:∵AE=BF,AB=AC,∴Rt△ABF≌Rt△CAE(HL),∴∠CAE=∠ABF,∵∠ABF+∠AFB=90°,∴∠CAE+∠AFB=90°,∴∠ADF=90°,即AE⊥BF.
如图,已知△ABC为等腰直角三角形,∠BAC=90°,且EC⊥AC于点C,AE=BF.试判断AE和BF的位置关系,并说明理由.
如图,有一直角三角形ABC，∠C＝90°，AC＝10cm，BC＝5cm，一条线段PQ＝AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等？
解：(1)当P运动到AP＝BC时，∵∠C＝∠QAP＝90°.在Rt△ABC与Rt△QPA中，∵PQ＝AB，AP＝BC，∴Rt△ABC≌Rt△QPA(HL)，∴AP＝BC＝5cm；
(2)当P运动到与C点重合时，AP＝AC. 在Rt△ABC与Rt△QPA中，∵PQ＝AB，AP＝AC，∴Rt△QAP≌Rt△BCA(HL)，∴AP＝AC＝10cm，∴当AP＝5cm或10cm时，△ABC才能和△APQ全等．
找对应边和对应角，分类讨论
斜边和一条直角边对应相等的两个直角三角形全等.
在直角三角形中，只要有两边对应相等，则直角三角形全等