数学八年级下册第一章 三角形的证明4 角平分线一等奖ppt课件

这是一份数学八年级下册第一章 三角形的证明4 角平分线一等奖ppt课件，共28页。PPT课件主要包含了PDPE，验证猜想，OPOP，∴PDPE，应用所具备的条件，定理的作用，证明线段相等，几何语言，∴EBFC，角平分线的性质等内容，欢迎下载使用。
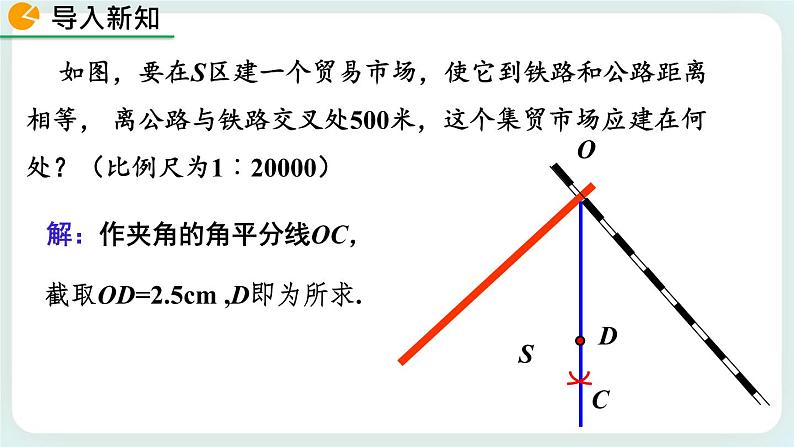
如图，要在S区建一个贸易市场，使它到铁路和公路距离相等， 离公路与铁路交叉处500米，这个集贸市场应建在何处？（比例尺为1︰20000）
解：作夹角的角平分线OC，
截取OD=2.5cm ,D即为所求.
1.会叙述角平分线的性质定理及判定定理.
2.能利用三角形全等，证明角平分线的性质定理，并理解和掌握定理及其逆定理.
3.能够应用这两个定理解决一些简单的实际问题.
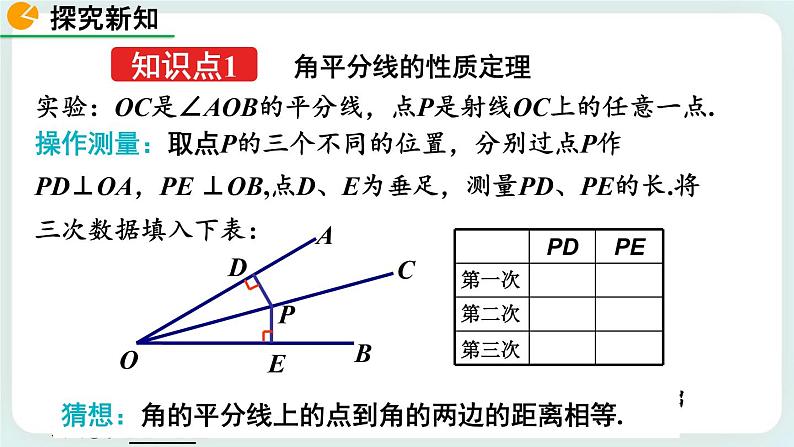
操作测量：取点P的三个不同的位置，分别过点P作PD⊥OA，PE ⊥OB,点D、E为垂足，测量PD、PE的长.将三次数据填入下表：
观察测量结果，猜想线段PD与PE的大小关系，写出结论：_____
实验：OC是∠AOB的平分线，点P是射线OC上的任意一点.
猜想：角的平分线上的点到角的两边的距离相等.
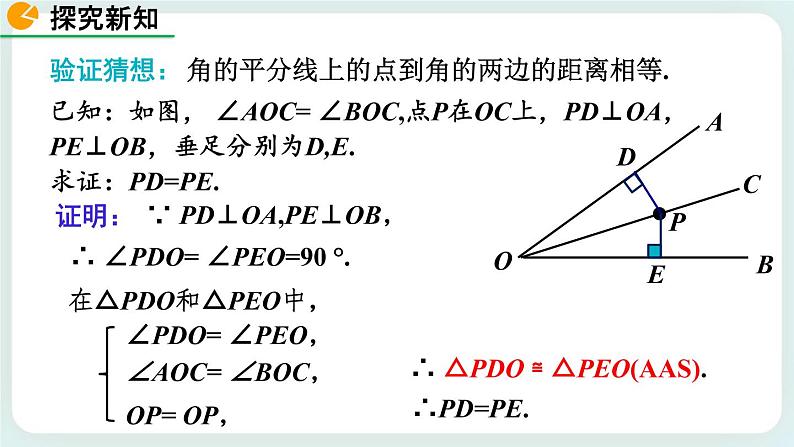
已知：如图， ∠AOC= ∠BOC,点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D,E.求证：PD=PE.
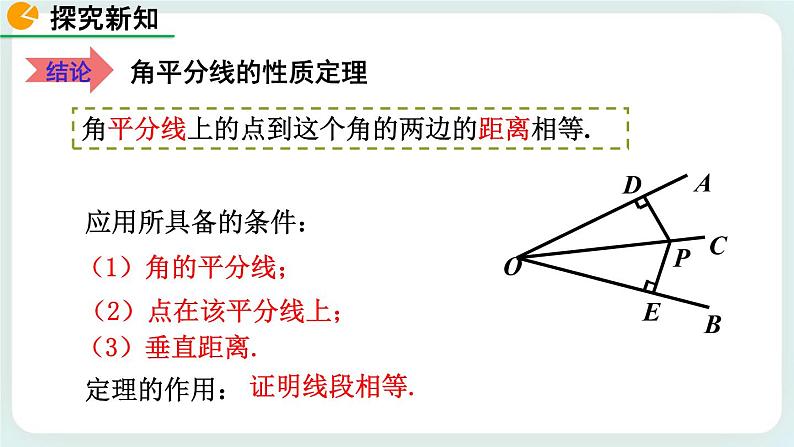
角的平分线上的点到角的两边的距离相等.
∵ PD⊥OA,PE⊥OB，
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中，
∠PDO= ∠PEO，
∠AOC= ∠BOC，
∴ △PDO ≌ △PEO(AAS).
角平分线上的点到这个角的两边的距离相等.
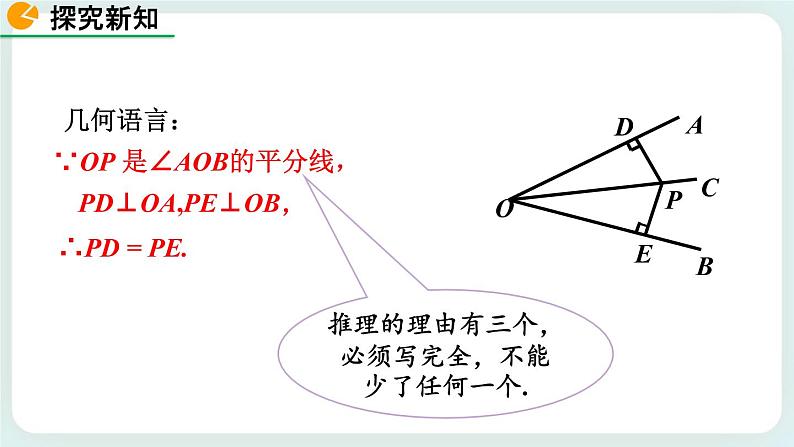
∵OP 是∠AOB的平分线，
推理的理由有三个，必须写完全，不能少了任何一个.
PD⊥OA,PE⊥OB，
证明：∵AD是∠BAC的角平分线，DE⊥AB, DF⊥AC，
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中，
∴ Rt△BDE ≌ Rt△CDF(HL).
如图，AM是∠BAC的平分线，点P在AM上，PD⊥AB，PE⊥AC，垂足分别是D、E，PD=4cm，则PE=______cm.
角的内部到角的两边距离相等的点在角的平分线上．
思考：交换角平分线性质中的已知和结论，你能得到什么结论？这个新结论正确吗？
思考：这个结论正确吗？
已知：如图，点P为∠AOB内一点，PD⊥OA，PE⊥OB，垂足分别是D、E，且PD=PE.求证：OP平分∠AOB.
∴OP平分∠AOB.
在Rt△PDO和Rt△PEO 中，
（全等三角形的对应角相等）.
OP=OP（公共边），
PD= PE（已知 ），
∵PD⊥OA,PE⊥OB，
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO（ HL）.
在一个角的内部，到角的两边距离相等的点在这个角的平分线上.
判断点是否在角平分线上.
∵ PD⊥OA,PE⊥OB，PD=PE.
∴点P 在∠AOB的平分线上.
解：∵DE⊥AB，DF⊥AC，垂足分别为E，F，且DE=DF，
∴ AD平分∠BAC.
又∵∠BAC=60°，∴∠BAD=30°，
∴ DE= AD= .
在Rt△ADE 中，∠AED=90°，AD=10，
如图所示，在△ABC中，AD是BC边的中线，DE⊥AB于点E，DF⊥AC于点F，且BE＝CF.求证：DA平分∠EDF.
证明：证法1：∵AD是△ABC的中线，∴BD＝CD.在Rt△BED和Rt△CFD中，∵BD＝CD，BE＝CF，∴Rt△BED≌Rt△CFD（HL），∴DE＝DF.又∵DE⊥AB，DF⊥AC，∴AD是∠BAC的平分线，即∠EAD＝∠FAD.又∵∠ADE＝90°－∠EAD，∠ADF＝90°－∠FAD，∴∠ADE＝∠ADF，即DA平分∠EDF.
证法2：同证法1，可得Rt△BED≌Rt△CFD.∴∠B＝∠C，∴AB＝AC.又∵BE＝CF，∴AE＝AF.又∵AE⊥DE，AF⊥DF， ∴DA平分∠EDF.
（2020·湘潭）如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD=3，点M是射线OC上一动点，则PM的最小值为 .
1.如图,在Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为________. 
2. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为(　 　)
A.3B.4C.5D.6
3. 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线, ∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD= (　 　)A.75° B.80°C.85° D.90°
4.如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是(　 　)A.①和②B.②和③　C.①和③D.全对
1、如图,BD是∠ABC的平分线,DE⊥AB于点E,△ABC的面积是30 cm2,AB=18 cm,BC=12 cm,则DE=______cm.
2、如图,△ABC的两条外角平分线AP,CP相交于点P,PH⊥AC于H;如果∠ABC=60°,则下列结论:①∠ABP=30°;②∠APC=60°;③PB=2PH;④∠APH=∠BPC,其中正确的结论个数是 (　 　)A.1　B.2C.3　D.4
如图，在Rt△ABC中，AC=BC,∠C＝90°，AP平分∠BAC交BC于点P，若PC＝4, AB=14.
(1)则点P到AB的距离为_______.
解：由角平分线的性质，可知，PD=PC=4，
(2)求△APB的面积.
(3)求∆PDB的周长.
一个点：角平分线上的点；二距离：点到角两边的距离；两相等：两条垂线段相等
过角平分线上一点向两边作垂线段
在一个角的内部，到角两边距离相等的点在这个角的平分线上