


还剩26页未读,
继续阅读
所属成套资源:北师大版数学八年级下册PPT课件全套
成套系列资料,整套一键下载
- 3.1 图形的平移(第1课时) 课件 课件 4 次下载
- 3.1 图形的平移(第2课时) 课件 课件 4 次下载
- 3.2 图形的旋转(第1课时) 课件 课件 6 次下载
- 3.2 图形的旋转(第2课时) 课件 课件 4 次下载
- 3.3 中心对称 课件 课件 4 次下载
数学1 图形的平移完整版ppt课件
展开
这是一份数学1 图形的平移完整版ppt课件,共34页。PPT课件主要包含了向上平移6个单位,向下平移5个单位,向左平移1个单位,向右平移3个单位,Axy,Bx-3y,向左平移3个单位,向上平移4个单位,-1-2,-2-1等内容,欢迎下载使用。
(1)(x,y)(x,y+6)
(2)(x,y)(x,y -5)
1、在坐标系中,将坐标作如下变化时,图形将怎样变化?
(4)(x,y)(x+3 , y)
(3)(x,y) (x-1 , y)
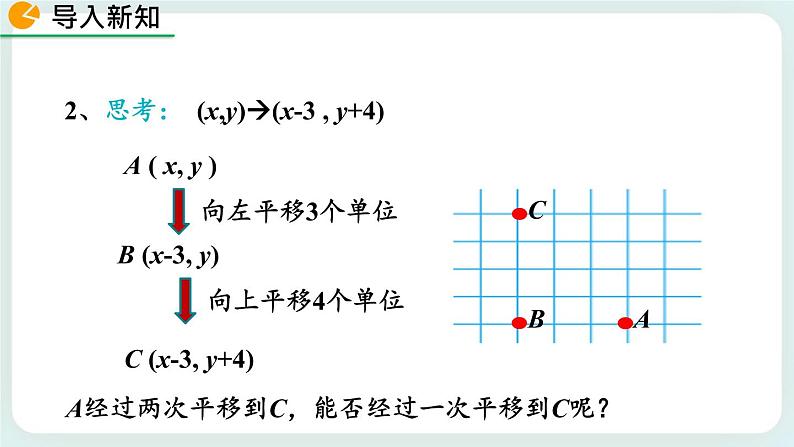
2、思考: (x,y)(x-3 , y+4)
C (x-3, y+4)
A经过两次平移到C,能否经过一次平移到C呢?
1. 掌握平面直角坐标系中图形的两次平移与一次平移的转化.
2. 掌握平移引起的点的坐标的变化规律.
3. 感受代数与几何的相互转化,初步建立空间观念.
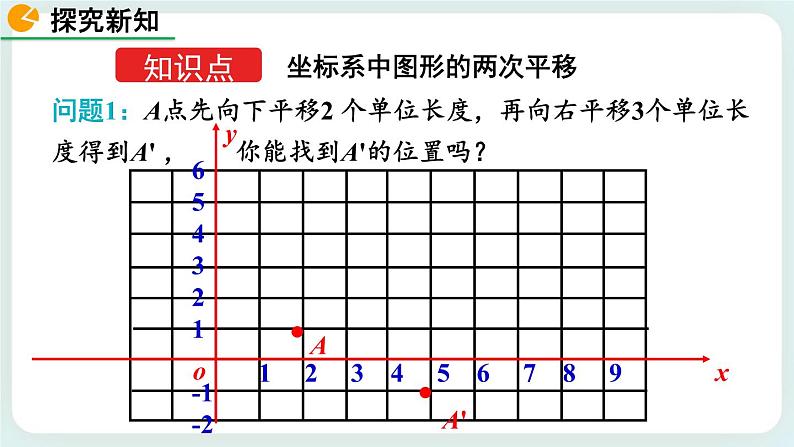
问题1:A点先向下平移2 个单位长度,再向右平移3个单位长度得到A' , 你能找到A'的位置吗?
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
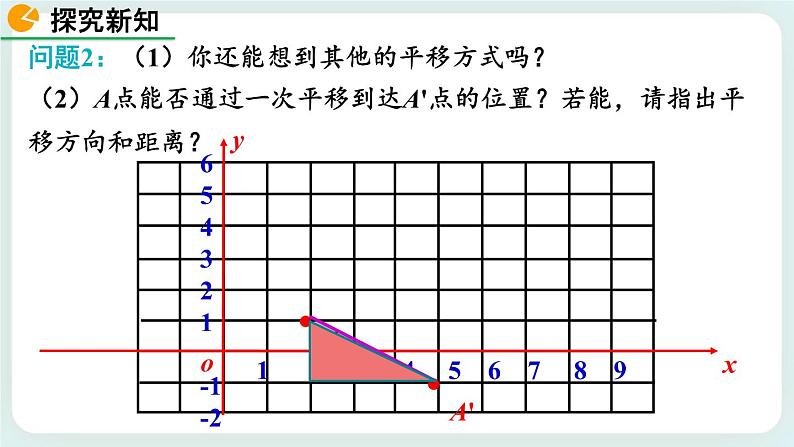
问题2:(1)你还能想到其他的平移方式吗?(2)A点能否通过一次平移到达A'点的位置?若能,请指出平移方向和距离?
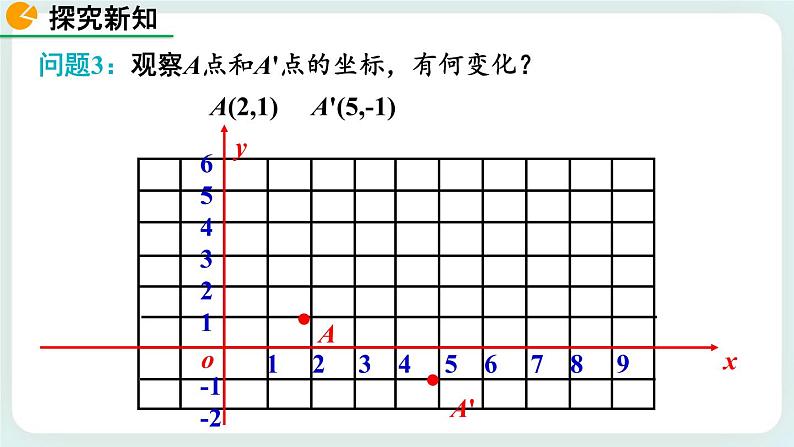
问题3:观察A点和A'点的坐标,有何变化? A(2,1) A'(5,-1)
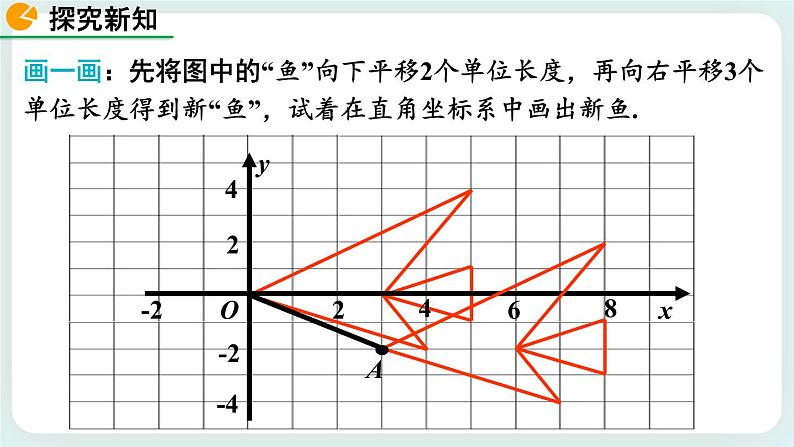
画一画:先将图中的“鱼”向下平移2个单位长度,再向右平移3个单位长度得到新“鱼”,试着在直角坐标系中画出新鱼.
(1)在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
平移方向是O到A,平移距离是OA= .
(2)对应点的坐标之间有什么关系?
横坐标加3,纵坐标减2.
做一做:先将右图中的“鱼” F的每个“顶点” 的横坐标分别加2,纵坐标不变,得到 “鱼” G;再将“鱼” G的每个“顶点” 的纵坐标分别加3,横坐标不变,得到“鱼” H.“鱼” H与原来的 “鱼” F相比有什么变化?能否将“鱼” H看成是“鱼” F经过一次平移得到的?与同伴交流.
结论:1.形状、大小相同,只是位置改变 ,先向右平移了2个单位长度,再向上平移了3个单位长度.
2.可以将“鱼”H看成是“鱼”F经过一次平移得到的,平移方向是点(0,0)到点(2,3)的方向,平移距离是 .
在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
思考:一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
注意:图形上一组对应点的平移方向和平移距离就是这个图形的平移方向和平移距离.
(0,-4)或(0,4)
解析:设点P到AB的距离为h,则 ,由S△PAB=S四边形ABDC,得2h=8,解得h=4,∴P(0,4)或(0,-4).
已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(-2,2)在经过此次平移后对应点A′(5,-4),则a-b-c+d的值为 ( )A.13B.-13C.1D.-1
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系?纵坐标呢?分别写出点A′,B′,C′,D′的坐标;
解:四边形A′B′C′D′与四边形ABCD对应点的横坐标分别增加了4,纵坐标分别增加了3,A′(1,8),B′(0,6),C′(3,4),D′(3,7).
(2)如果四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:平移方向A到A′,如图所示;平移距离AA',由勾股定理得AA'=5.
两次平移所得图形的坐标变化(1)遵循上加下减,左减右加的平移规律.(2)对应点连线的方向就是图形平移的方向,对应点连线的线段长度就是平移的距离.
如图,△ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将△ABC作同样的平移得到△A1B1C1.求A1、B1、C1的坐标.
P1(x0+2,y0+4)
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6); B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3); C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
(2020·绵阳)平面直角坐标系中,将点A(-1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为 .
1.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )A.(﹣1,1) B. (﹣1,﹣2) C. (﹣1,2) D. (1,2)
2.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
3.在平面直角坐标系内,线段CD是由线段AB平移得到的,点A(-2,3)的对应点为点C(2,-2),则点B(-4,1)的对应点D的坐标为( )A.(-6,-4) B.(-4,0)C.(6,-4) D.(0,-4)
4.下面所说的“平移”,是指只沿方格的格线(即左右或上下)运动,并将图中的任意一条线段平移一格称为“1步”.通过平移,使得图中的3条线段首尾相接组成一个三角形,最少需要移动的步数是( )A.7步B.8步C.9步D.10步
5.在如图所示的直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为 ( )
A.(-0.4,-1)B.(-1.5,-1)C.(-1.6,-1)D.(-2.4,-2)
1、已知:如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6.如果将△ABC在直线AB上平行移动2个单位后得△A′B′C′,那么△CA′B的面积为 .
解析:本题需要讨论向左平移还是向右平移,然后分别求出△CA′B的面积即可.∵在Rt△ABC中,∠ACB=90°,AC=BC,AB=6.∴△ABC的高CD=3,
①当向右平移时,S△CA′B= BA′·CD=6.
②当向左平移时,S△CA′B= BA′·CD=12.答案:6或12.
2、如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.(1)分别写出△DEF各顶点的坐标.
解:∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.∴D(2,9),E(1,5),F(4,6).
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:连接AD,∵由图可知,AD= =5,∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.
解:(1)AB=4-1=3,点C到AB的距离为3- ,∴S△ABC= ×3×(3- )= .
解:(2)让各点的横坐标不变,纵坐标减 ,各点的坐标为:A′(1, - ),B′(4, - ),C′(3,3- ).(3)∵平移不改变图形的大小,∴S△A′B′C′=S△ABC= .
沿x轴、y轴的两次平移
(1)(x,y)(x,y+6)
(2)(x,y)(x,y -5)
1、在坐标系中,将坐标作如下变化时,图形将怎样变化?
(4)(x,y)(x+3 , y)
(3)(x,y) (x-1 , y)
2、思考: (x,y)(x-3 , y+4)
C (x-3, y+4)
A经过两次平移到C,能否经过一次平移到C呢?
1. 掌握平面直角坐标系中图形的两次平移与一次平移的转化.
2. 掌握平移引起的点的坐标的变化规律.
3. 感受代数与几何的相互转化,初步建立空间观念.
问题1:A点先向下平移2 个单位长度,再向右平移3个单位长度得到A' , 你能找到A'的位置吗?
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9
问题2:(1)你还能想到其他的平移方式吗?(2)A点能否通过一次平移到达A'点的位置?若能,请指出平移方向和距离?
问题3:观察A点和A'点的坐标,有何变化? A(2,1) A'(5,-1)
画一画:先将图中的“鱼”向下平移2个单位长度,再向右平移3个单位长度得到新“鱼”,试着在直角坐标系中画出新鱼.
(1)在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
平移方向是O到A,平移距离是OA= .
(2)对应点的坐标之间有什么关系?
横坐标加3,纵坐标减2.
做一做:先将右图中的“鱼” F的每个“顶点” 的横坐标分别加2,纵坐标不变,得到 “鱼” G;再将“鱼” G的每个“顶点” 的纵坐标分别加3,横坐标不变,得到“鱼” H.“鱼” H与原来的 “鱼” F相比有什么变化?能否将“鱼” H看成是“鱼” F经过一次平移得到的?与同伴交流.
结论:1.形状、大小相同,只是位置改变 ,先向右平移了2个单位长度,再向上平移了3个单位长度.
2.可以将“鱼”H看成是“鱼”F经过一次平移得到的,平移方向是点(0,0)到点(2,3)的方向,平移距离是 .
在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
思考:一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
注意:图形上一组对应点的平移方向和平移距离就是这个图形的平移方向和平移距离.
(0,-4)或(0,4)
解析:设点P到AB的距离为h,则 ,由S△PAB=S四边形ABDC,得2h=8,解得h=4,∴P(0,4)或(0,-4).
已知△ABC内一点P(a,b)经过平移后对应点P′(c,d),顶点A(-2,2)在经过此次平移后对应点A′(5,-4),则a-b-c+d的值为 ( )A.13B.-13C.1D.-1
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系?纵坐标呢?分别写出点A′,B′,C′,D′的坐标;
解:四边形A′B′C′D′与四边形ABCD对应点的横坐标分别增加了4,纵坐标分别增加了3,A′(1,8),B′(0,6),C′(3,4),D′(3,7).
(2)如果四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:平移方向A到A′,如图所示;平移距离AA',由勾股定理得AA'=5.
两次平移所得图形的坐标变化(1)遵循上加下减,左减右加的平移规律.(2)对应点连线的方向就是图形平移的方向,对应点连线的线段长度就是平移的距离.
如图,△ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将△ABC作同样的平移得到△A1B1C1.求A1、B1、C1的坐标.
P1(x0+2,y0+4)
解:A(-3,2)经平移后得到(-3+2,2+4),即A1(-1,6); B(-2,-1)经平移后得到(-2+2,-1+4),即B1(0,3); C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
(2020·绵阳)平面直角坐标系中,将点A(-1,2)先向左平移2个单位,再向上平移1个单位后得到的点A1的坐标为 .
1.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )A.(﹣1,1) B. (﹣1,﹣2) C. (﹣1,2) D. (1,2)
2.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
3.在平面直角坐标系内,线段CD是由线段AB平移得到的,点A(-2,3)的对应点为点C(2,-2),则点B(-4,1)的对应点D的坐标为( )A.(-6,-4) B.(-4,0)C.(6,-4) D.(0,-4)
4.下面所说的“平移”,是指只沿方格的格线(即左右或上下)运动,并将图中的任意一条线段平移一格称为“1步”.通过平移,使得图中的3条线段首尾相接组成一个三角形,最少需要移动的步数是( )A.7步B.8步C.9步D.10步
5.在如图所示的直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为 ( )
A.(-0.4,-1)B.(-1.5,-1)C.(-1.6,-1)D.(-2.4,-2)
1、已知:如图,在Rt△ABC中,∠C=90°,AC=BC,AB=6.如果将△ABC在直线AB上平行移动2个单位后得△A′B′C′,那么△CA′B的面积为 .
解析:本题需要讨论向左平移还是向右平移,然后分别求出△CA′B的面积即可.∵在Rt△ABC中,∠ACB=90°,AC=BC,AB=6.∴△ABC的高CD=3,
①当向右平移时,S△CA′B= BA′·CD=6.
②当向左平移时,S△CA′B= BA′·CD=12.答案:6或12.
2、如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.(1)分别写出△DEF各顶点的坐标.
解:∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.∴D(2,9),E(1,5),F(4,6).
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
解:连接AD,∵由图可知,AD= =5,∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.
解:(1)AB=4-1=3,点C到AB的距离为3- ,∴S△ABC= ×3×(3- )= .
解:(2)让各点的横坐标不变,纵坐标减 ,各点的坐标为:A′(1, - ),B′(4, - ),C′(3,3- ).(3)∵平移不改变图形的大小,∴S△A′B′C′=S△ABC= .
沿x轴、y轴的两次平移













