初中数学北师大版七年级下册1 认识三角形完美版课件ppt

这是一份初中数学北师大版七年级下册1 认识三角形完美版课件ppt，共23页。PPT课件主要包含了三角形，等边三角形，想一想，cm或21cm，+9+9，三边长，基础巩固题，或85，完成下列各题等内容，欢迎下载使用。

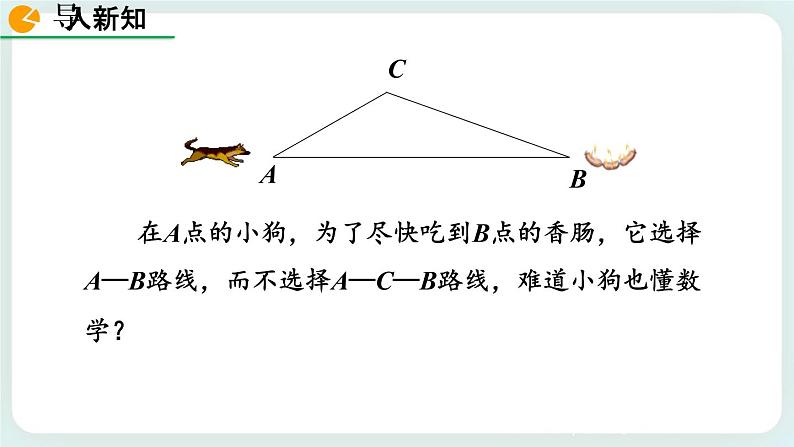
在A点的小狗，为了尽快吃到B点的香肠，它选择A—B路线，而不选择A—C—B路线，难道小狗也懂数学？
1. 记住等腰三角形、等边三角形的有关概念，会对三角形按边进行分类.
2. 知道“三角形中任意两边的和大于第三边”，运用关系解决简单的实际问题.
3.培养学生的观察、分析、比较、操作能力，进一步发展空间观念，提高学生的探索能力.
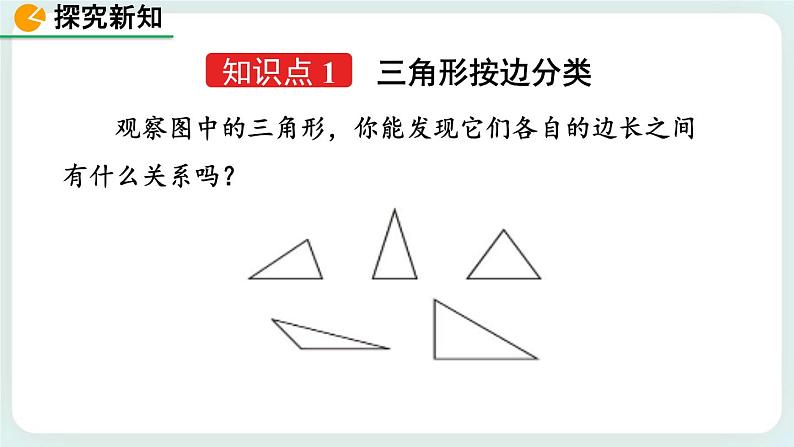
观察图中的三角形，你能发现它们各自的边长之间有什么关系吗？
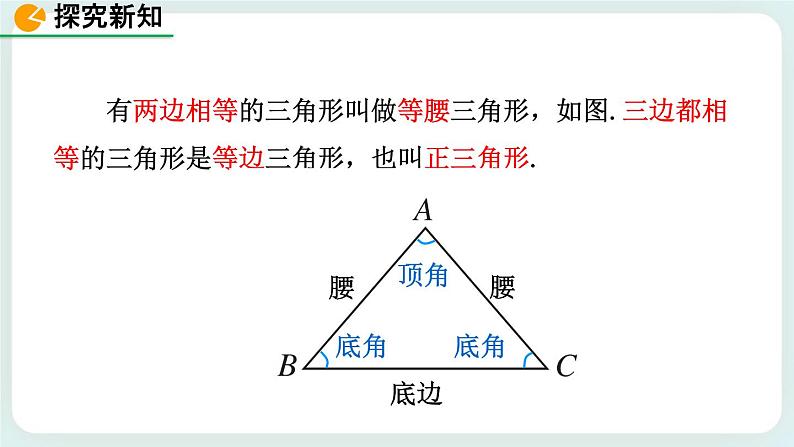
有两边相等的三角形叫做等腰三角形，如图.三边都相等的三角形是等边三角形，也叫正三角形.
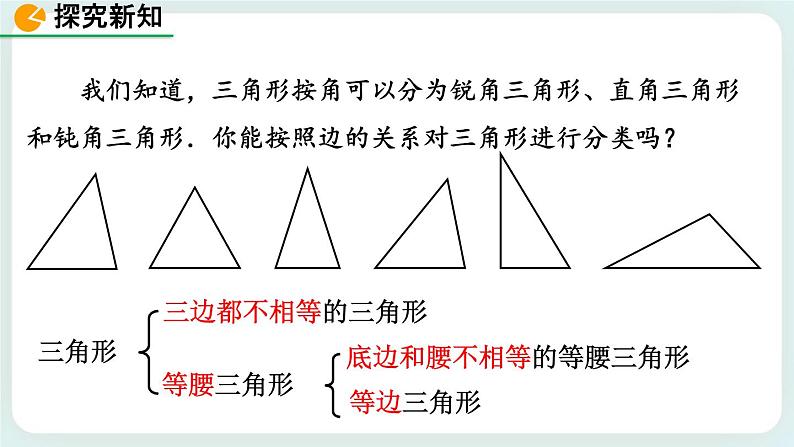
我们知道，三角形按角可以分为锐角三角形、直角三角形和钝角三角形．你能按照边的关系对三角形进行分类吗？
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
下列说法正确的有(　 　)①等腰三角形是等边三角形;②三角形按边可分为等腰三角形、等边三角形和不等边三角形;③等腰三角形至少有两边相等;④三角形按角可分为锐角三角形、直角三角形和钝角三角形.A.①②　　 B.①③④ C.③④　 D.①②④
（1）元宵节的晚上，房梁上亮起了彩灯，装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢？说明你的理由． （2）在一个三角形中，任意两边之和与第三边的长度有怎样的关系？为什么？
三角形任意两边之和大于第三边
计算三角形的任意两边之差，并与第三边比较，你能得到什么结论？
三角形任意两边之差小于第三边
如图三角形中，假设小狗要从点B出发沿着三角形的边跑到点C，它有几条路线可以选择？各条路线的长一样吗？
路线1:由点B到点C.
路线2:由点B到点A，再由点A到点C .
两条路线长分别是BC,AB+AC.
由“两点之间，线段最短”可以得到AB+AC >BC . 有“三角形任意两边之差小于第三边”可得：AB>BC-AC .
同理可得：AC+BC >AB,AB+BC >AC（AC >AB-BC，BC >AC-AB）
三角形的三边有这样的关系： （1） 三角形两边的和大于第三边; （2） 三角形两边的差小于第三边.
有两根长度分别为 5 cm和 8 cm的木棒，用长度为 2 cm的木棒与它们能摆成三角形吗？为什么？长度为13 cm的木棒呢？
解：取长度为2cm的木棒时，由于2+5 =7＜8，出现了两边之和小于第三边的情况，所以它们不能摆成三角形． 取长度为13cm的木棒时，由于5+8=13，出现了两边之和等于第三边的情况，所以它们也不能摆成三角形．
提示：只要满足较小的两条线段之和大于第三条线段，便可构成三角形;若不满足，则不能构成三角形.
下列长度的各组线段能否组成一个三角形？(1) 15cm、10cm、7cm (2) 4cm、5cm、10cm(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm
(2) 因为4cm+5cm<10cm，所以这三条线段不能组成一个三角形.
(3) 因为3cm+5cm=8cm， 所以这三条线段不能组成一个三角形.
(4) 因为4cm+5cm>6cm，所以这三条线段能组成一个三角形.
例 用一根长为18厘米的细铁丝围成一个等腰三角形.（1）如果腰长是底边的2倍，那么各边的长是多少？（2）能围成有一边的长为4厘米的等腰三角形吗？为什么？
解：(1) 设底边长为x厘米，则腰长为2x厘米 x+2x+2x=18. 解得x=3.6 所以三边长分别为3.6厘米，7.2厘米，7.2厘米.
(2) 因为长为4厘米的边可能是腰，也可能是底边，所以需要分情况讨论.(a) 如果4厘米长为底边，设腰长为x厘米，则4+2x=18，解得x=7.(b) 如果4厘米长为腰，设底边长为x厘米，则2×4+x=18,解得x=10. 因为4+4＜10，出现两边和小于第三边的情况，所以不能围成腰长为4厘米的等腰三角形.由以上结论可知，可以围成底边长是4厘米的等腰三角形.
三角形三边的关系解答实际问题
（1）如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=___________.
（2）如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.
1.（2020•绍兴）长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形（木棒允许连接，但不允许折断），得到的三角形的最长边长为（　　）A．4 B．5 C．6 D．7
2.（2020•济宁）已知三角形的两边长分别为3和6，则这个三角形的第三边长可以是_______（写出一个即可）．
1.下列各组数中，能作为一个三角形三边边长的是（　 ）A．1，1，2B．1，2，4C．2，3，4D．2，3，5
2.已知等腰三角形的两边长分别为8cm，3cm，则这三角形的周长为（　 ） 　A. 14cm　 B.19cm C. 14cm或19cm D. 不确定
3.下列说法：①等边三角形是等腰三角形；②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形；③三角形的两边之差大于第三边；④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有（ ）A.1个B.2个C.3个D.4个
4.一个等腰三角形的周长为24cm，只知其中一边的长为7cm，则这个等腰三角形的腰长为_________cm.
（3）以长为3cm、5cm、7cm、10cm的四条线段中的三条线段为边，可构成_____个三角形．
（1）任何三条线段都能组成一个三角形 ( )
（2）因为a+b>c,所以a，b，c三边可以构成三角形（ ）
等腰三角形的周长为20厘米.（1）若已知腰长是底长的2倍，求各边的长；（2）若已知一边长为6厘米，求其他两边的长.
解：（1）设底边长为x厘米，则腰长为2x 厘米. x + 2x + 2x = 20, 解得 x = 4.所以三边长分别为4cm，8cm，8cm.（2）如果6 厘米长的边为底边，设腰长为x 厘米，则6 + 2x = 20，解得x = 7；如果6厘米长的边为腰，设底边长为x 厘米，则2×6 + x = 20，解得x = 8.由以上讨论可知，其他两边的长分别为7 厘米，7 厘米或6 厘米，8 厘米.
如图，有四个村庄(点)A，B，C，D，要建一所学校O，使OA+OB+OC+OD最小，画图说明O在哪里，并说出你的理由.
解:要使OA+OB+OC+OD最小，则点O是线段AC，BD的交点.理由如下：如果存在不同于点O的交点P，连接PA，PB，PC，PD，那么PA+PC＞AC，即PA+PC＞OA+OC，同理，PB+PD＞OB+OD，则PA+PB+PC+PD＞OA+OB+OC+OD，即点O是线段AC，BD的交点时，OA+OB+OC+OD最小.
三角形两边的和大于第三边．
三角形两边的差小于第三边．