数学七年级下册1 认识三角形精品课件ppt

这是一份数学七年级下册1 认识三角形精品课件ppt，共22页。PPT课件主要包含了复习导入，BEEC，cm²，∠1∠2，所以∠1等内容，欢迎下载使用。

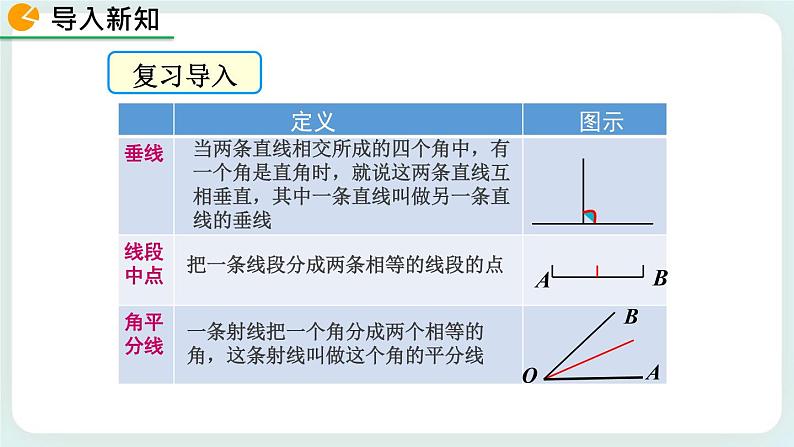
当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线
1. 了解三角形的中线、角平分线等有关概念.
2. 掌握任意三角形的中线、角平分线的画法，通过观察认识到三角形的三条中线、三条角平分线分别交于一点.
3. 提高学生动手操作及解决问题的能力.
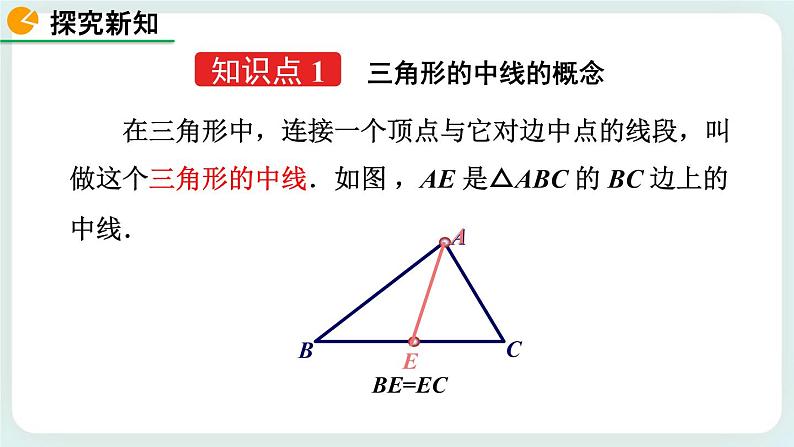
在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线．如图 ，AE 是△ABC 的 BC 边上的中线．
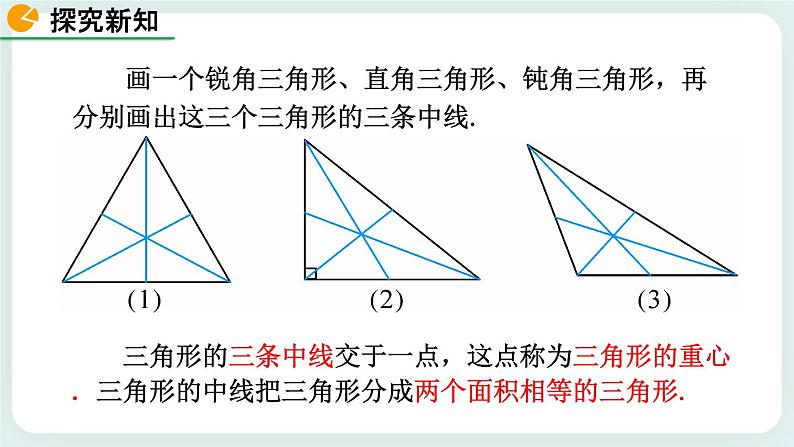
议一议：（1）在纸上画出一个锐角三角形，并画出它的三条中线，它们有怎样的位置关系？与同伴进行交流．（2）钝角三角形和直角三角形的三条中线也有同样的位置关系吗？折一折，画一画，并与同伴进行交流．
　　画一个锐角三角形、直角三角形、钝角三角形，再分别画出这三个三角形的三条中线.
三角形的三条中线交于一点，这点称为三角形的重心．三角形的中线把三角形分成两个面积相等的三角形.
例 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为(　 　)　A.19 cm　 B.22 cm　 C.25 cm　 D.31 cm
解析：因为AD是BC边上的中线,所以BD=CD,所以△ABD和△ACD周长的差=(AB+BD+AD)-(AC+CD+AD)=AB-AC.因为△ABD的周长为25 cm,AB比AC长6 cm,所以△ACD的周长为25-6=19(cm).
点拨：根据三角形中线的定义,把三角形周长的差转化为已知两边AB,AC的长度的差是解题的关键.
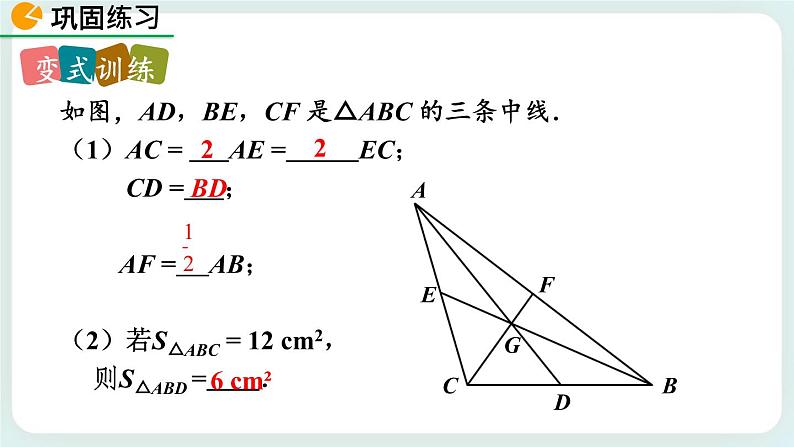
如图，AD，BE，CF 是△ABC 的三条中线．（1）AC = AE = EC； CD = ； AF = AB；（2）若S△ABC = 12 cm2， 则S△ABD = ．
在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．如图 ，AD 是△ABC 的一条角平分线．
注意：“三角形的角平分线”是一条线段.
做一做：每人准备锐角三角形、钝角三角形和直角三角形纸片各一个．（1）你能分别画出这三个三角形的三条角平分线吗？（2）你能用折纸的办法得到它们吗？（3）在每个三角形中，这三条角平分线之间有怎样的位置关系？将你的结果与同伴进行交流．
三角形的三条角平分线交于同一点.
解：因为AD是△ABC的角平分线，∠BAC＝68°，所以∠DAC＝∠BAD＝34°.在△ABD中， ∠B+∠ADB+∠BAD＝180°，所以∠ADB＝180°－∠B－∠BAD ＝180°－36°－34°＝110°.
例 如图,在△ABC中,∠BAC=68°，∠B=36°，AD是△ABC的一条角平分线，求∠ADB的度数.
如图，AD，BE，CF 是△ABC 的三条角平分线，则： ∠1 = ； ∠3 = ； ∠ACB = 2 .
如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=30°，∠2=20°，则∠B=_____.
解析：因为AE平分∠BAC，所以∠1=∠EAD+∠2，所以∠EAD=∠1-∠2=30°-20°=10°.Rt△ABD中，∠B=90°-∠BAD =90°-30°-10°=50°.
（2020•营口）如图，AB∥CD，∠EFD=64°，∠FEB的角平分线EG交CD于点G，则∠GEB的度数为（　　）A．66°B．56°C．68°D．58°
1.如图，在△ABC中有四条线段DE，BE，EF，FG，其中有一条线段是△ABC的中线，则该线段是（　　）A．线段DE B．线段BE C．线段EF D．线段FG
2．在△ABC中，AD为中线，BE为角平分线，则在以下等式中：①∠BAD=∠CAD；②∠ABE=∠CBE；③BD=DC；④AE=EC．其中正确的是 （　　）A．①② B．③④ C．①④ D．②③
3.如图所示，在△ABC中，D，E，F是BC边上的三点，且∠1=∠2=∠3=∠4，AE是哪个三角形的角平分线( ) A.△ABE B.△ADF C.△ABC D.△ABC，△ADF
在△ABC中,CD是中线,已知BC－AC=5cm, △DBC的周长为25cm,求△ADC的周长.
解：因为CD是△ABC的中线，所以BD＝AD，所以△DBC的周长＝BC＋BD＋CD＝25cm，则BD+CD＝25－BC.所以△ADC的周长＝AD＋CD＋AC ＝BD＋CD＋AC ＝25-BC＋AC＝25－(BC－AC) ＝25－5＝20cm.
如图，在△ABC中，BP,CP分别是∠B, ∠C的平分线，试说明： ∠BPC= 90˚+ ∠A.
因为BP，CP分别是∠B， ∠C的平分线，(已知)
因为∠BPC +∠1 + ∠2 =180˚,
∠A +∠ABC +∠ACB=180˚,
所以∠BPC=180˚−(∠1 +∠2 )